1. Introduction
In this tutorial, we’ll talk about Generative Adversarial Networks (GANs), an unsupervised deep-learning approach. Mainly, we’ll walk through the architecture of the two principal models that form a GAN, the Generator, and Discriminator models. We’ll also analyze the dominant behavior between the two models through their loss function.
2. Generative Adversarial Networks
GAN is a machine-learning framework that was first introduced by Ian J. Goodfellow in 2014. In general, a GAN’s purpose is to learn the distribution and pattern of the data in order to be able to generate synthetic data from the original dataset that can be used in realistic occasions. The authors of the paper presented an algorithm in which two neural networks that are trained simultaneously, the generator and the discriminator, compete with each other, forming an adversarial game. The architecture of the GAN framework looks as follows:
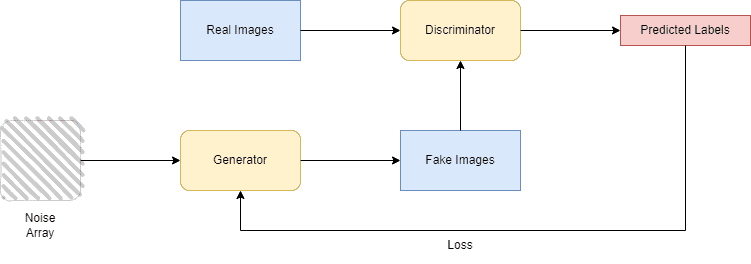
The task of the generator is to create synthetic (fake) data from the original, while the discriminator’s task is to decide whether its input data is original or created from the generator. The training of the two models continues until the generator is able to imitate the original data at a level that the discriminator struggles to classify the data as fake or original.
2.1. GAN’s Loss Function
The generator (G) and discriminator (D) try out a game of two players in which the first attempts to minimize and the second to maximize the value (V) of the loss function:
![\[\underset{G}{min} \; \underset{D}{max} \; V(D,G) = \mathbb{E}_{x} [log \; D (x) ] + \mathbb{E}_{z} [log (1 - D (G(z))) ] \]](/wp-content/ql-cache/quicklatex.com-ef3b041fbb3e7baff78baf103cb9c892_l3.svg "Rendered by QuickLaTeX.com")
where 
denote the generator’s output when it receives as input noise 
, the discriminator’s probability that the original data 
is real, and the discriminator’s probability that a synthetic sample 
of data is real, and 
, 
denote the mean likelihood over all original data and synthetic data respectively.
In the above equation, we notice that during the training of the discriminator (D) focuses on maximizing the 
, which means achieving the correct label (real or synthetic) during the classification of 
, while, the generator (G) focuses on minimizing 
and cannot directly influence 
.
3. The Generator
The generator is responsible for producing new sufficient synthetic data that cannot be distinguished from the original by studying the distribution of the real input. During the training of the generator’s neural network, it receives that valid data along with noise and creates new data from that synthesis, which is received directly by the discriminator, which makes a decision about the validation of each sample and classifies it as synthetic or real.
3.1. The Generator’s Reward
After the discriminator’s classification, the generator receives the decision made by the first and acts accordingly. In case the discriminator classifies the data incorrectly, the generator prevails in the competitive game between them, gets rewarded, and therefore has a greater contribution to the loss function. Otherwise, the generator loses and receives a penalty. The training of the generator focuses on updating and minimizing:
![\[\nabla_{\theta_{g}} \frac{1}{m} \sum_{i=1}^{m} log (1 - D(G(z^{(i)})))\]](/wp-content/ql-cache/quicklatex.com-429676046a12ceec5b2a620faa2afa66_l3.svg "Rendered by QuickLaTeX.com")
where the notations are the same as above and 
is a hyperparameter of a multilayer perception that represents a differentiable function 
which maps input noise to data space.
4. The Discriminator
The discriminator is responsible for classifying data across two classes, synthetic or real. During the training of the discriminator’s neural network, it receives data (real and synthetic) produced by the generator and is asked to decide about its validation. In the early stages, the discriminator’s work is easy because the generator cannot produce indistinguishable samples. Therefore discriminator is able to classify samples with high confidence.
4.1. The Discriminator’s Reward
In case of a correct decision, the discriminator prevails in the min-max game. Otherwise, it loses and receives a penalty. The training of the discriminator focuses on updating and maximizing:
![\[\nabla_{\theta_{g}} \frac{1}{m} \sum_{i=1}^{m}[ log \; D(x^{(i)})+ log (1 - D(G(z^{(i)})))]\]](/wp-content/ql-cache/quicklatex.com-0e06ca22420a8f23111d99b29c4eab40_l3.svg "Rendered by QuickLaTeX.com")
where the notations are the same as above.
5. Limitations of GAN
Generative Adversarial Networks can achieve an important performance and are a wise choice for training a semi-supervised classifier, but they may struggle on certain occasions. First of all, the two neural networks must be well synchronized during the training, and each model must not be trained continuously without the other. Moreover, they need a wide variety of data in order for the generator to produce a wide range of outputs and increase the overall model’s accuracy. Also, GANs struggle to generate discrete data from text or speech.
6. Applications
GANs can be applied in a wide variety of applications where new plausible data is needed. Particularly, GANs are mainly used in creating new images and videos, which may be about generation photographs of human faces or poses, realistic photographs, or even cartoon characters and emojis.
The generated output can be used in marketing, games, or for scientific and studying purposes, where datasets and benchmarks are hard to find due to standardized data protection.
7. Conclusion
In this article, we walked through GAN, a semi-supervised framework for creating synthetic data from real. In particular, we discussed in detail the two main neural networks, the generator and the discriminator, and talked about how they play a competitive min-max game trying to replicate a probability distribution. We mainly focused on how each model’s loss function is affected, and in case the model gets rewarded or penalized. Finally, we mentioned some limitations and applications of a GAN.