F-Beta Score | Baeldung on Computer Science

1. Introduction

There are several metrics for evaluating machine-learning (ML) models. One that we often calculate when analyzing classifiers is the $F_1$ score, which combines precision and recall into a single value.

In this tutorial, we’ll talk about its generalization, the $F_{\beta}$ score, which can give more weight to either recall or precision.

2. The F1 Score

The F1 score of a classifier is the harmonic mean of its precision $\boldsymbol{P}$ and recall $\boldsymbol{R}$ :

(1) $\begin{equation*} F_1 = \frac{1}{\frac{1}{2}\left(\frac{1}{P} + \frac{1}{R} \right)} = \frac{2PR}{P+R} \end{equation*}$

It’s useful because it’s high when both scores are large, as we see in its contour plot:

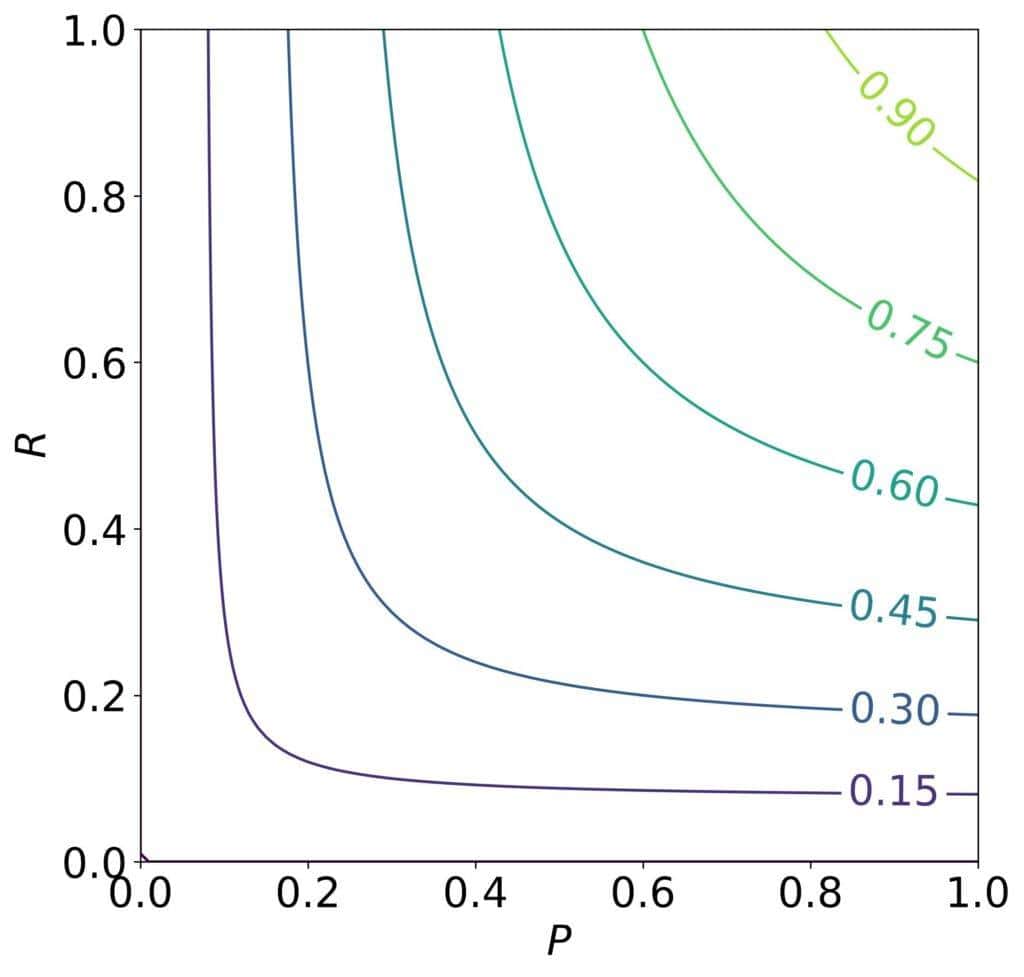
It gives equal weights to recall and precision, so the contours are symmetric around the 45-degree line,

2.1. What if Precision and Recall Aren’t Equally Important?

However, there are cases where one of the scores is more important than the other.

We care more about recall if a false negative is more severe an error than a false positive. Automated diagnostic ML tools in medicine illustrate that. There, a false negative is a missed condition, which could be fatal for our patient’s health. In contrast, a false-positive diagnosis induces stress, but additional testing can relieve the patient.

Conversely, precision is more important when a false positive has a higher cost. That’s the case in spam detection. Letting a spam e-mail appear in the inbox may annoy the user, but marking a non-spam e-mail as spam and sending it to thrash could result in the loss of a job opportunity.

In such applications, we’d like to have a metric that considers the relative importance of $P$ and $R$ . The $F_{\beta}$ score does precisely that.

3. The F-Beta Score

The common formulation of $F_{\beta}$ is:

(2) $\begin{equation*} F_{\beta} = (1+\beta^2)\frac{PR}{\beta^2 P + R} \end{equation*}$

It’s a weighted harmonic mean of $P$ and $R$ which uses $\frac{1}{\beta^2+1}$ and $\frac{\beta^2}{\beta^2+1}$ as the weights:

(3) $\begin{equation*} \frac{1}{\frac{1}{\beta^2+1}\frac{1}{P} + \frac{\beta^2}{\beta^2+1}\frac{1}{R}} \end{equation*}$

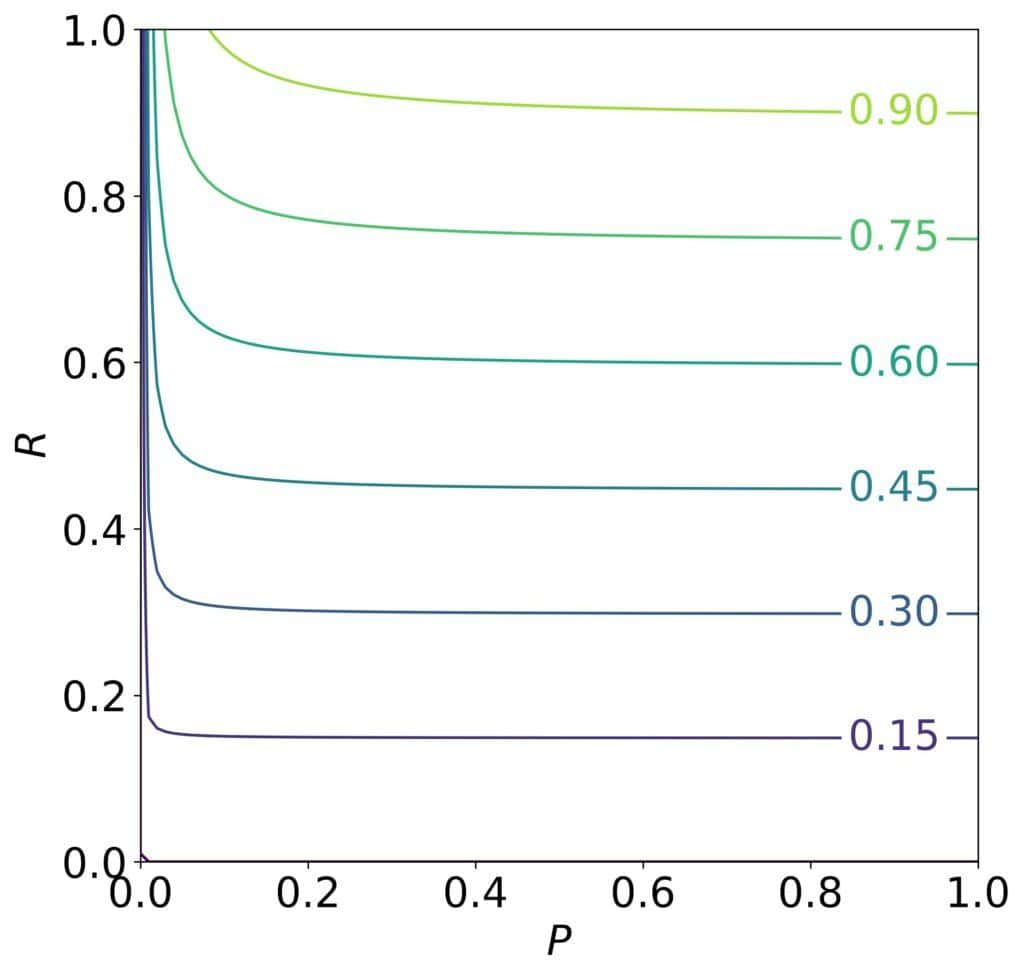
If $\boldsymbol{\beta > 1}$ , the recall is $\boldsymbol{\beta}$ times more important than precision, and if $\boldsymbol{\beta < 1}$ , it’s the other way around. As the contours for $\beta=10$ show, we can get a high $F_{1}$ score if the recall is high enough no matter if the precision is low, which aligns with our requirements:

But why does $\beta^2$ figure in the equations instead of $\beta$ ? Isn’t the latter more intuitive?

3.1. Relative Importance of Precision and Recall

The reason why we have $\beta^2$ instead of $\beta$ lies in how the relative importance was defined when $F_{\beta}$ was first formulated.

In general, the weighted harmonic mean of $R$ and $P$ using $w$ and $1-w$ as the weights is:

(4) $\begin{equation*} F = \frac{1}{\frac{1-w}{P} + \frac{w}{R}} \end{equation*}$

To get $F_{\beta}$ from $F$ , we require the latter to satisfy the condition of relative importance. More precisely, we want $w$ to be such that at the points at which $P$ and $R$ equally contribute to $F$ , $R$ is $\beta$ times $P$ .

Mathematically, that means that the ratio $\boldsymbol{\frac{R}{P}}$ should be equal to $\boldsymbol{\beta}$ when the partial derivatives $\boldsymbol{\frac{\partial F}{\partial R}}$ and $\boldsymbol{\frac{\partial F}{\partial P}}$ are the same.

3.2. Derivation

Let’s first find the derivatives:

(5) $\begin{equation*} \begin{aligned} \frac{\partial F}{\partial R} &= - \frac{1}{\left( \frac{1-w}{P} + \frac{w}{R}\right)^2} \times \frac{-w}{R^2} = \frac{w}{\left( \frac{1-w}{P} + \frac{w}{R}\right)^2 R^2} \\ \\ \frac{\partial F}{\partial P} &= - \frac{1}{\left( \frac{1-w}{P} + \frac{w}{R}\right)^2} \times \frac{-(1-w)}{P^2} = \frac{1-w}{\left( \frac{1-w}{P} + \frac{w}{R}\right)^2 P^2} \end{aligned} \end{equation*}$

From $\frac{\partial F}{\partial P}=\frac{\partial F}{\partial R}$ , we get:

(6) $\begin{equation*} \begin{aligned} \frac{1-w}{\left( \frac{1-w}{P} + \frac{w}{R}\right)^2 P^2} &= \frac{w}{\left( \frac{1-w}{P} + \frac{w}{R}\right)^2 R^2} \\ \frac{R^2}{P^2} & = \frac{w}{1-w} \\ \end{aligned} \end{equation*}$

Requiring the ratio $\frac{R}{P}$ to be $\beta$ , we solve $\frac{R^2}{P^2}=\beta^2$ for $w$ :

(7) $\begin{equation*} \begin{aligned} \frac{w}{1-w} &= \beta^2 \\ w &= \beta^2 - \beta^2 w \\ (1+\beta^2) w &= \beta^2 \\ w &= \frac{\beta^2}{1+\beta^2} \end{aligned} \end{equation*}$

Plugging in $w$ into the weighted harmonic mean, we get $F_{\beta}$ as defined by Equations (2) and (3).

3.3. The Effect of Importance

Let’s analyze what happens to $F_{\beta}$ as we vary $\beta$ .

Setting $\boldsymbol{\beta}$ to 1, we get the usual $\boldsymbol{F_1}$ . That covers the case with $R$ and $P$ having equal weights.

If only recall is important, we let $\boldsymbol{\beta \rightarrow \infty}$ . In that case, we expect $F_{\beta}$ to reduce to $R$ . Taking the limit, we get:

(8) $\begin{equation*} F_{\infty} = \lim_{\beta \rightarrow \infty} F_{\beta} = \lim_{\beta \rightarrow \infty} \frac{1}{\frac{1}{\beta^2+1}\frac{1}{P} + \frac{\beta^2}{\beta^2+1}}\frac{1}{R}} = \frac{1}{0 \times \frac{1}{P} + 1 \times \frac{1}{R}} = R \end{equation*}$

Similarly, if we care only about precision, we set $\boldsymbol{\beta}$ to 0:

(9) $\begin{equation*} F_{0} = (1 + 0) \frac{PR}{0 \times P + R} = \frac{PR}{R} = P \end{equation*}$

The values of $\beta$ between 0 and $\infty$ represent intermediate cases.

4. Alternative Formulation of the F-Beta Score

A different definition of relative importance would yield a different $\boldsymbol{F_{\beta}}$ score.

For instance, we could say that if we consider the recall score to be $\beta$ times more important than precision, that means that when $P=R$ , increasing $R$ improves $F$ $\beta$ times as much as an equal increase in $P$ .

Mathematically, this translates to the following condition:

(10) $\begin{equation*} P = R \implies \frac{\partial F}{\partial R} = \beta \times \frac{\partial F}{\partial P} \end{equation*}$

Solving for $w$ , we get:

(11) $\begin{equation*} \begin{aligned} \frac{w}{\left( \frac{1-w}{R} + \frac{w}{R}\right)^2 R^2} &= \beta \times \frac{1-w}{\left( \frac{1-w}{R} + \frac{w}{R}\right)^2 R^2} \\ w &= \beta (1 - w) \\ w + \beta w &= \beta \\ w &= \frac{\beta}{1 + \beta} \end{aligned} \end{equation*}$

From there, we get a metric that is linear in $\beta$ :

(12) $\begin{equation*} \tilde{F}_{\beta} = \frac{1}{\frac{1}{1+\beta}\frac{1}{P} + \frac{\beta}{1 + \beta} \frac{1}{R}} = (1 + \beta)\frac{PR}{ \beta P + R} \end{equation*}$

It too reduces to $F_1$ when $\beta=1$ but uses a different definition of relative importance than the version with $\beta^2$ .

5. Conclusion

In this article, we talked about the $F_{\beta}$ score. We use it to evaluate classifiers when the recall and precision aren’t equally important. For instance, that’s the case in spam detection and medicine.

However, the two scores’ relative importance we quantify with $\beta$ has a formal mathematical definition: when their partial derivatives are equal, recall is $\beta$ times as large as precision.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex