F-1 Score for Multi-Class Classification

1. Introduction

In this tutorial, we’ll talk about how to calculate the F-1 score in a multi-class classification problem. Unlike binary classification, multi-class classification generates an F-1 score for each class separately.

We’ll also explain how to compute an averaged F-1 score per classifier in Python, in case a single score is desired.

2. F-1 Score

F-1 score is one of the common measures to rate how successful a classifier is. It’s the harmonic mean of two other metrics, namely: precision and recall. In a binary classification problem, the formula is:

The F-1 Score metric is preferable when:

• We have imbalanced class distribution
• We’re looking for a balanced measure between precision and recall (Type I and Type II errors)

As the F-1 score is more sensitive to data distribution, it’s a suitable measure for classification problems on imbalanced datasets.

3. Multi-Class F-1 Score Calculation

For a multi-class classification problem, we don’t calculate an overall F-1 score. Instead, we calculate the F-1 score per class in a one-vs-rest manner. In this approach, we rate each class’s success separately, as if there are distinct classifiers for each class.

As an illustration, let’s consider the confusion matrix below with a total of 127 samples:

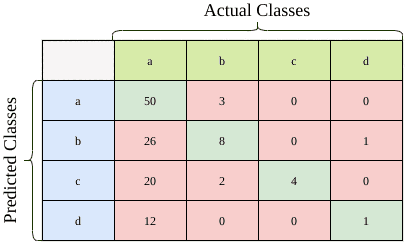
Now let’s calculate the F-1 score for the first class, which is class a. We first need to calculate the precision and recall values:

Then, we apply the formula for class a:

Similarly, we first calculate the precision and recall values for the other classes:

The calculations then lead to per-class F-1 scores for each class:

4. Implementation

In the Python sci-kit learn library, we can use the F-1 score function to calculate the per class scores of a multi-class classification problem. 

We need to set the average parameter to None to output the per class scores.

For instance, let’s assume we have a series of real y values (y_true) and predicted y values (y_pred). Then, let’s output the per class F-1 score:

from sklearn.metrics import f1_score
f1_score(y_true, y_pred, average=None)

In our case, the computed output is:

array([0.62111801, 0.33333333, 0.26666667, 0.13333333])

On the other hand, if we want to assess a single F-1 score for easier comparison, we can use the other averaging methods. To do so, we set the average parameter.

Here we’ll examine three common averaging methods.

The first method, micro calculates positive and negative values globally:

f1_score(y_true, y_pred, average='micro')

In our example, we get the output:

0.49606299212598426

Another averaging method, macro, take the average of each class’s F-1 score:

f1_score(y_true, y_pred, average='macro')

gives the output:

0.33861283643892337

Note that the macro method treats all classes as equal, independent of the sample sizes.

As expected, the micro average is higher than the macro average since the F-1 score of the majority class (class a) is the highest.

The third parameter we’ll consider in this tutorial is weighted. The class F-1 scores are averaged by using the number of instances in a class as weights:

f1_score(y_true, y_pred, average='weighted')

generates the output:

0.5728142677817446

In our case, the weighted average gives the highest F-1 score.

We need to select whether to use averaging or not based on the problem at hand.

5. Conclusion

In this tutorial, we’ve covered how to calculate the F-1 score in a multi-class classification problem.

Firstly, we described the one-vs-rest approach to calculate per class F-1 scores.

Also, we’ve covered three ways of calculating a single average score in Python.