Exponential Search | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll explain the Exponential Search algorithm.

2. Unbounded Search

In a classical search problem, our goal is to find the index of a value $z$ in an $n$ -element sorted array $x$ ( $x[i] \leq x[i+1]$ for $i=1,2,\ldots, n-1$ ). For instance, we can use the Binary Search algorithm to look for any $z$ in a logarithmic time.

However, there are cases when Binary Search isn’t fast enough or even possible to use. For example, if $n$ is so large that $x$ can’t fit into memory and even $O(\log n)$ is unacceptably high, or if we don’t have an array to search but a function $f$ defined over an infinite integer domain. In the latter case, we have an infinite collection $[x_m] = \{ f(m)\}$ to search, so we’re solving an unbounded search problem. In the former case, $x$ is technically finite, but since it’s too large for our memory, we deal with it as if it’s unbounded.

We can’t use Binary Search since it assumes that its input is a finite array. One of the methods we can use is the Exponential Search algorithm. It assumes that we can evaluate (or find) $x_m$ for any integer $m$ in the search domain and that $x$ is sorted.

3. Exponential Search

Exponential Search has two phases.

The first phase finds the portion of $x$ that contains $z$ if it’s present in the array. More specifically, the first phase finds the number $j$ such that $x[2^j] \leq z < x[2^{j+1}]$ .

The idea is to partition $x$ into sub-arrays of incremental sizes and check them consecutively until we find the one that can contain $z$ . The boundary indices of those sub-arrays are powers of 2, hence the algorithm’s name:

In the second phase, the algorithm looks for $\boldsymbol{z}$ in $\boldsymbol{x[2^j:(2^{j+1}-1)]=[x[2^j], x[2^j+1], x[2^j+2], \ldots, x[2^{j+1} - 1]]}$ using Binary Search.

3.1. Pseudocode

Here’s the pseudocode:

So, we first check if $x[1] \leq z < x[2]$ , which simplifies to testing if $x[1] = z$ . If the test fails, we check if $x[2] \leq z < x[4]$ . If that isn’t the case, we test if $x[4] \leq z < x[8]$ , then $x[8] \leq z < x[16]$ , $x[16] \leq z < x[32]$ , and so on until we find the boundaries that capture $z$ : $x[2^j] \leq z < x[2^{j+1}]$ .

Afterward, we run Binary Search on $x[2^j:(2^{j+1}-1)]$ . If it doesn’t find $z$ , then it isn’t an element of $x$ . If it does, it will return the index of $z$ in the sub-array as an integer from 1 to $2^j$ . We adjust it to get the index of $z$ in the entire array by adding the offset $2^j$ (the starting index of the sub-array) and taking away 1.

3.2. Example

Let’s say we’re looking for a number at the 17th position in a very long array $x$ . By testing the boundaries with the Exponential Search, we locate the portion of $x$ that contains the number in 5 steps:

4. Complexity

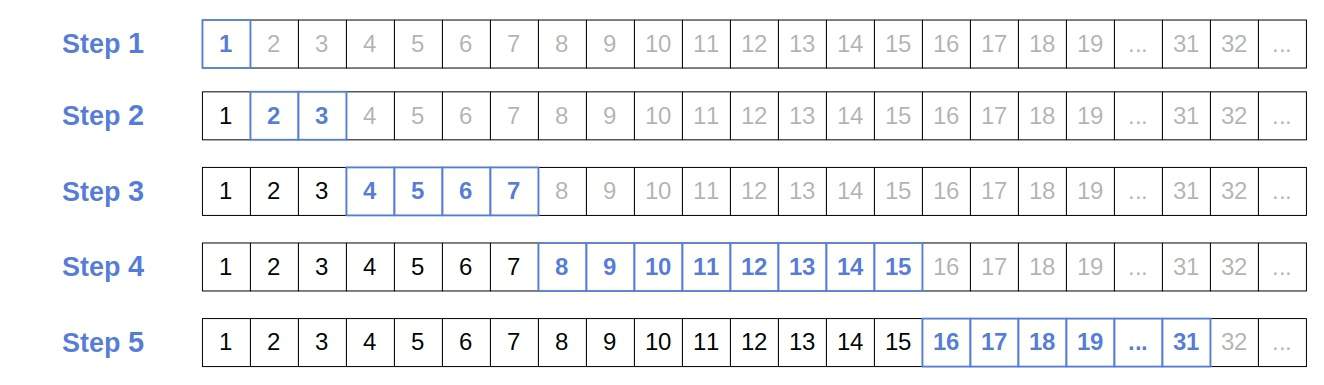
If $m$ is the index of $z$ in $x$ , the time complexity of the first phase is $O(\log m)$ , as illustrated in the example above.

In the second phase, we run Binary Search on the sub-array whose size is:

$2^{1 + \lfloor \log m \rfloor} - 2^{\lfloor \log m \rfloor} = 2 \times 2^{\lfloor \log m \rfloor} - 2^{\lfloor \log m \rfloor} = 2^{\lfloor \log m \rfloor}$

The time complexity of Binary Search is $O(\log n)$ for an array of size $n$ , so the complexity of the second phase of Exponential Search is:

$O \left( \log \left( 2^{\lfloor \log m \rfloor} \right) \right) = O( \log m)$

So, the total combined runtime complexity of both phases is $O(\log m) + O(\log m) = O(\log m)$ .

From there, we see that Exponential Search pays off in the cases when $x$ is very large, and the sought element is near the arrays’ beginning.

5. Conclusion

In this article, we presented Exponential Search. It’s a search algorithm we use to find values in unbounded collections like ordered ranges of functions defined over natural numbers. Additionally, we can also use it to search arrays too big to fit into memory.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex