Implementation of Elitism in Evolutionary Algorithms

1. Overview

In evolutionary algorithms, we use the concept of elitism to select the best-performing individuals from one generation and transfer them directly to the next generation without applying mutation or crossover operations.

Moreover, the primary purpose of the elitism method is to preserve the best solutions and maintain diversity in the population. As a result, the elitism method helps to improve the convergence speed and robustness of evolutionary algorithms.

In this tutorial, we’ll discuss how to implement the elitism method in evolutionary algorithms in detail using Python.

2. Generating Initial Population

We start an evolutionary algorithm by generating an initial population. Furthermore, the initial population consists of individuals representing the solution space of an optimization problem. Typically, we model each individual as a string of 0s and 1s, but the representation can vary depending on the given problem.

To generate the initial population in Python, we first import the random module. Furthermore, we specify the size of the population and the length of the binary string representing each individual:

import random
population_s = 15
individual_s = 6

Therefore, the initial population contains 15 individuals with a length of 6.

Now, we define a function in Python that generates the population with 15 individual binary strings:

def generate_p(population_s, individual_s):
    p = []
    for _ in range(population_s):
        indi = ''.join([random.choice('01') for _ in range(individual_s)])
        p.append(indi)
    return p

Moreover, we add a print statement to display the initial population:

print("The generated Initial population is:", generate_p(15, 6))

Finally, let’s take a look at the output:

The generated Initial population is: ['000101', '101000', '111101', '000101', '010000',
  '000010', '110000', '110001', '001000', '011010', '111000', '100010', '001000', '110101', '111100']

Thus, based on the given problem, we can change the initial population size and the length of the individuals.

3. Implementation of Fitness Function

After the initial generation of the population, the next step is to define a fitness function. In particular, the fitness function’s role is crucial in evolutionary algorithms as it measures the quality of each individual by assigning a numerical number. Moreover, the number is assigned based on the individual’s suitability to become an acceptable solution to the given problem.

Let’s assume we have a problem where the more one an individual contains, the more suitable the individual is to become a solution. Therefore, considering the given problem, let’s implement a simple fitness function that counts the number of 1 in each individual:

def fitness_function(indi):
    ft = indi.count('1')
    return ft

Furthermore, we implement a function that uses the fitness function that we defined and calculate the fitness score of the individuals in the initial population:

def calculate_fitness(p): 
    ft_scores = [] 
    for indi in p: 
        ft_scores.append(fitness_function(indi)) 
    return ft_scores
print("Fitness scores are:", ft_scores)

Finally, let’s see the fitness scores of the individuals:

Fitness scores are: [2, 2, 5, 2, 1, 1, 2, 3, 1, 3, 3, 2, 1, 4, 4]

Based on the fitness scores, we can select a particular individual or a set of individuals to proceed to the next step.

4. Selection Elite Individuals

After calculating the fitness scores, we apply the elitism approach to select top individuals from the initial population. Here, we pick the top 20% of the individuals with the highest fitness score:

def selection_elitism(p, ft_scores):
    sorted_ft_scores = sorted(zip(p, ft_scores), key=lambda x: x[1], reverse=True)
    t1 = int(len(sorted_ft_scores) * 0.2)
    elite_indi = [i for i, (indi, score) in enumerate(sorted_ft_scores) if score >= sorted_ft_scores[t1][1]]

Furthermore, based on the given problem and requirement, we can vary the percentage of individuals we pick from the initial population. Moreover, we implement a function to display the elite individuals:

print("The elite individuals and their fitness scores:")
    for i, (indi, score) in enumerate(sorted_ft_scores[0:t1]):
        print(f"Individual {i+1} ({indi}): Fitness score {score}")
elite_indi(p, ft_scores)

Thus, let’s display the top 20% of elite individuals from the initial population:

Top elite individuals and their fitness scores:
Individual 3 (111101): Fitness score 5
Individual 14 (110101): Fitness score 4
Individual 15 (111100): Fitness score 4

According to the elitism approach, the top 20% of the individuals we pick from the initial population will directly move to the next generation of the population without any change.

5. Crossover and Mutation

After we select the top elite individuals, the rest go through some operations to generate the next population generation. Therefore, to increase the quality of individuals for the next generation, we use two operators: crossover and mutation.

5.1. Implementation of Crossover

In the crossover operation, first, we select two parent chromosomes and a crossover point. Furthermore, based on this selection, we exchange genetic information or chromosomes to generate two new individuals who inherit traits from both parents:

def crossover_operation(pr1, pr2):
    cross_p = random.randint(0, len(pr1))
    new_indi1 = pr1[:cross_p] + pr2[cross_p:]
    new_indi2 = pr2[:cross_p] + pr1[cross_p:]
    return new_indi1, new_indi2
pr1 = [0, 0, 0, 1, 0, 1]
pr2 = [1, 0, 1, 0, 0, 0]
new_indi1, new_indi2 = crossover_operation(pr1, pr2)
print("New Individual 1:", new_indi1)
print("New Individual 2:", new_indi2)

In this case, we randomly selected the crossover point: cross_p. Hence, after we complete the crossover process, we get two new individuals for the next generation of the population:

New Individual 1: [0, 0, 1, 0, 0, 0]
New Individual 2: [1, 0, 0, 1, 0, 1]

Similarly, we can select a different pair of individuals from the initial population and generate a pair of new individuals using the crossover operation.

5.2. Implementation of Mutation

Moving forward, we can also use the mutation operation to generate a new population from the initial population. Furthermore, in the mutation process, we randomly alter some values from the individual of the initial population. Thus, it introduces diversity and helps evolutionary algorithms find optimal solutions faster.

To implement the mutation operation, we need to define a mutation probability. Therefore, in this implementation, we define the mutation probability as 10%. Additionally, for each bit of the individual bitstring, we generate a random number between 0 and 1 utilizing random.random() function. Hence, if the random number is less than the defined mutation probability, we flip the bit:

def mutation_operation(indi, mutation_p):
    mutated_indi = indi.copy()
    for i in range(len(mutated_indi)):
        if random.random() < mutation_p:
            mutated_indi[i] = 1 - mutated_indi[i]
    return mutated_indi
chromosome = [1, 0, 1, 0, 1, 0]
mutation_p = 0.1
mutated_indi = mutation_operation(indi, mutation_p)
print("Original individual bitstring:", indi)
print("Mutated individual bitstring:", mutation_operation)

After the completion of the mutation process, we get the new mutated individual for the next generation of the population:

Original individual bitstring: 101010
Mutated individual bitstring: 100110

Finally, we can apply the mutation operation to all the individuals in the initial population to generate new individuals for the new population.

6. Generation of New Population and Adding Elite Individuals

At this point, we have picked the top individuals from the initial population by implementing the concept of elitism. Furthermore, we explored how to apply the crossover and mutation operation to generate new individuals for the new population. Now, let’s see an example of how the elitism concept works in practice:

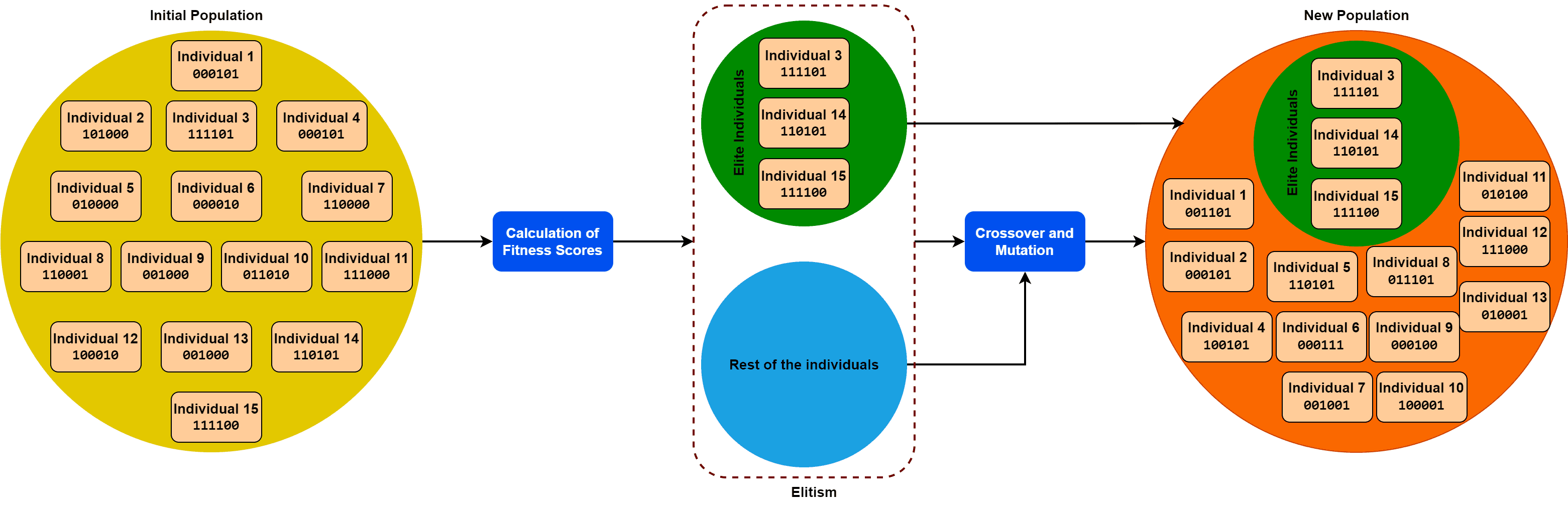
Hence, in this implementation, we picked three individuals from the initial population based on their fitness scores. The rest of the individuals go through the crossover and mutation process. Via the crossover and mutation process, we modify the bits and exchange bits between individuals to boost the probability of finding optimal solutions.

However, as we can see, we add the elite individuals from the initial population to the new population without changing any bits.

7. Conclusion

In this article, we discussed the details of implementing the elitism concept in evolutionary algorithms using Python. Additionally, we explored the intermediate steps and presented the implementation details of the selection, crossover, and mutation operation.