Tracing the Path in DFS, BFS, and Dijkstra’s Algorithm

1. Introduction

In this tutorial, we’ll show how to trace paths in three algorithms: Depth-First Search, Breadth-First Search, and Dijkstra’s Algorithm. More precisely, we’ll show several ways to get the shortest paths between the start and target nodes in a graph, and not just their lengths.

2. Tracing the Path in Recursive Depth-First Search

Depth-First Search (DFS) comes in two implementations: recursive and iterative. Tracing the shortest path to the target node in the former is straightforward. We only have to store the nodes as we unfold the recursion after reaching the target node:

Here, we treated $path$ as an array and prepended the nodes to it to have them in the order from the start node to the target. An alternative would be to use a stack. However, if the order doesn’t matter, we can avoid using a separate data structure for the path. We can print the current node as soon as it passes the $target$ test and keep printing $v$ in the if statements executed in the for-loops after returning from the recursive calls until we return to $s$ . That way, we avoid using additional memory.

2.1. Example

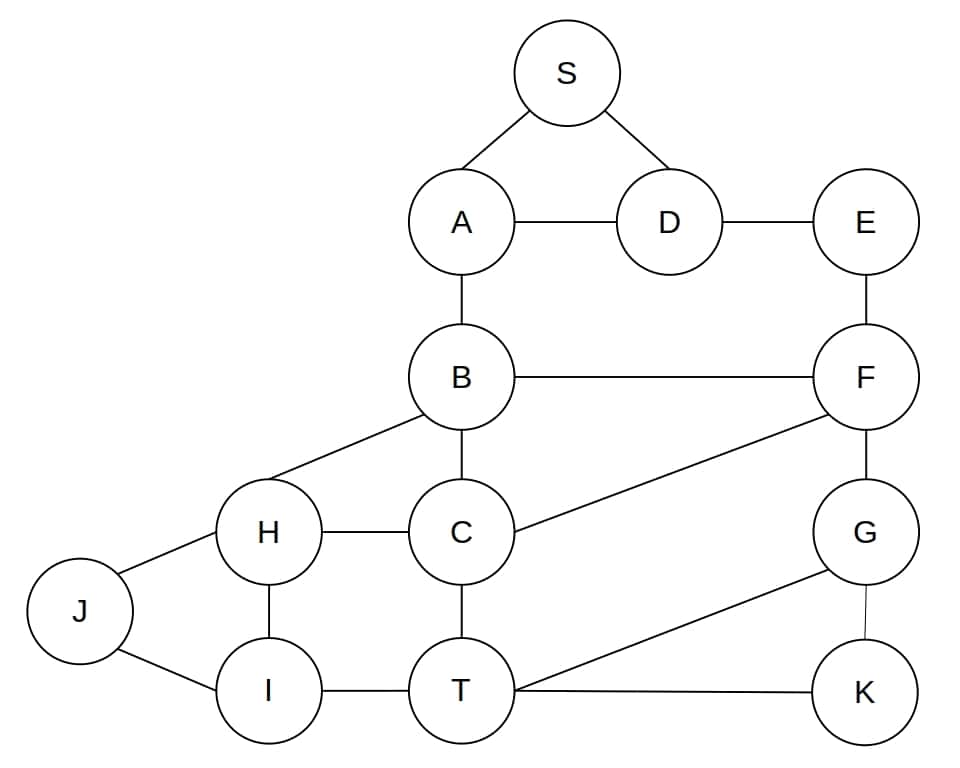
Let’s use the following graph as an example:

We want the shortest path from $S$ to $T$ . Expanding the children of a node in the proper order, DFS finds the shortest path between $S$ and $T$ :

Then, it returns $[T]$ to the call in which it expanded $C$ and prepends $C$ to $[T]$ to get $[C, T]$ . Doing the same with $B$ and $A$ , DFS returns $[A, B, C, T]$ to the original call, prepends $S$ to it, and gives us $[S, A, B, C, T]$ as the shortest path.

3. Tracing the Path in Iterative Depth-First Search

However, recursive DFS may be slower than the iterative variant:

There are two ways we can trace the path in the iterative DFS. In one approach, after visiting a node, we memorize which node its parent is in the search tree. That way, after finding the target node, we can reconstruct the path by following the parent-child hierarchy. In the other method, we store the full path to each node. Thus, when the search ends, the one leading to the target node is available as well.

We can implement both techniques using different data structures, with or without recursion. All the ways work the same, and which one we’ll choose is largely a matter of our preference.

3.1. Memorizing the “Family Ties”

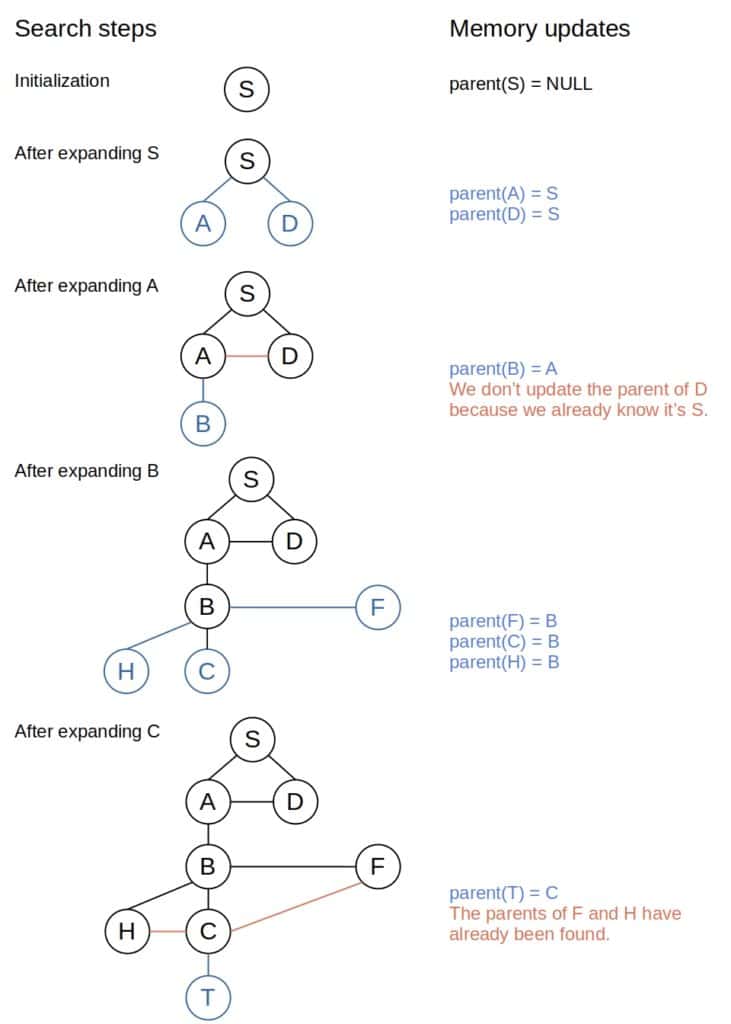
The key idea is to memorize the parents of the nodes we explore. Let’s say that we expanded a node $u$ and identified its children $v_1, v_2, \ldots, v_m$ . For each child, we have to memorize that its parent is $u$ :

3.2. Reconstructing the Path

Then, to reconstruct the path, we only have to read the memory to get the target’s parent, its parent afterward, and so on until we reach the start node:

This way, we get the path from the target node to the start node. If we want it the other way around, then we should print the path in reverse:

3.3. How to Implement the Memory

We can represent the information that $\boldsymbol{u}$ is the parent of $\boldsymbol{v}$ using different data structures. For example, we can store a pointer to $\boldsymbol{u}$ in $\boldsymbol{v}$ . Then, reading the memory amounts to traversing a linked list.

We can also use hash maps. A common approach is to assign a unique positive integer to each node as its id, treat the ids as indices, and store the parent-child information in an array. Let’s say that $memory$ is that array. Then, the parent of node $i$ is the node whose id is $memory[i]$ . Its parent is $memory[memory[i]]$ , and so on.

3.4. Example

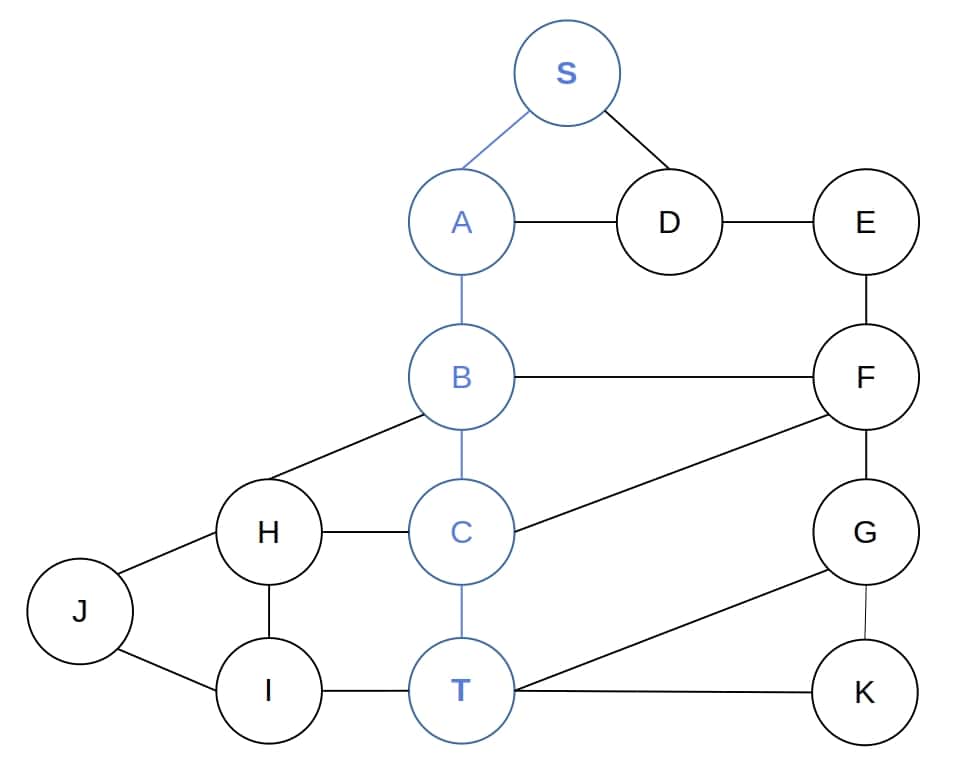
This is DFS would grow $memory$ if it expanded the nodes in the order which corresponds to the shortest bath between $S$ and $T$ :

3.5. Memorizing the Path While Searching

We can also keep track of the paths to the currently active nodes while running DFS. After expanding the node $\boldsymbol{u}$ , we remember the paths to the children of $\boldsymbols{u}$ that are its children in the search tree, and once the algorithm identifies a target node, we know we already have the path to it. Therefore, we don’t have to reconstruct it from the memorized information:

This approach is similar to path tracing in the recursive DFS. However, we use more memory because we keep the full paths to all the nodes in the $\bodsymbol{frontier}$ . In the recursive DFS, we only keep track of one path.

3.6. Example

This approach would work like this on the previous example:

4. Tracing the Path in Breadth-First Search

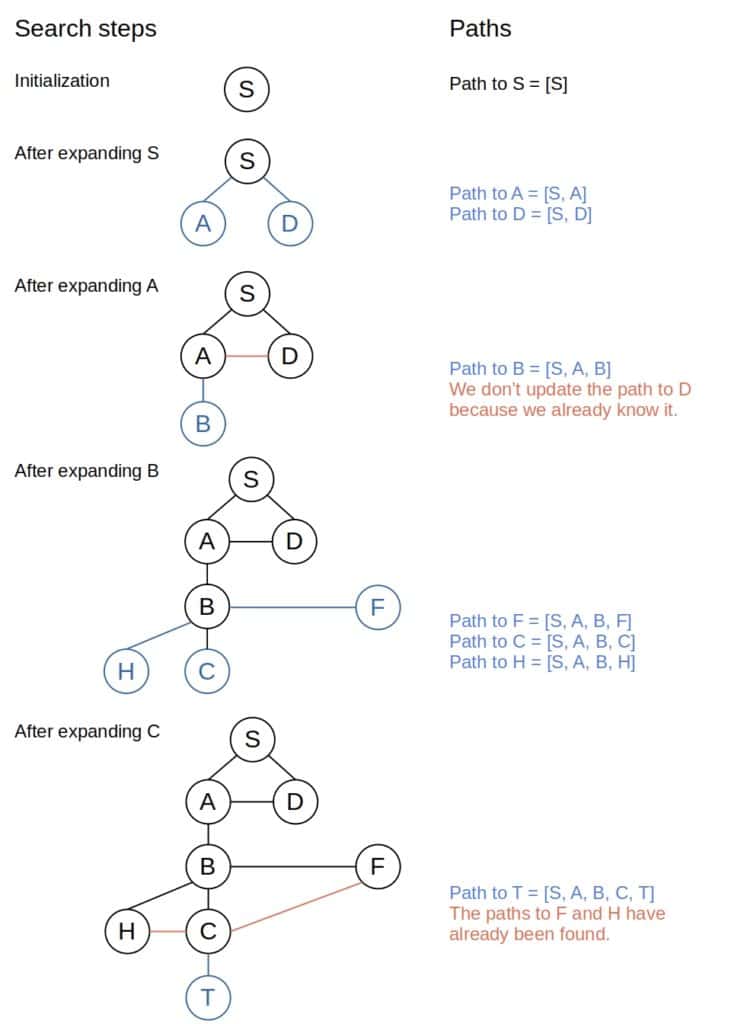
The same approaches that we used for DFS work as well for Breadth-First Search (BFS). The only algorithmic difference between DFS and BFS lies in the queue: the former uses a LIFO, whereas the latter uses a FIFO implementation. However, that causes BFS to use way more memory than DFS, so path storing may not be our best option. Instead, we should consider extending the nodes with the pointers to their parents or use a hash map. That method won’t induce much memory overhead:

We reconstruct the path just as in Algorithm 5. The only thing we should pay attention to is that the line “ $u \leftarrow$ find the parent of $u$ in $memory$ ” in Algorithm 5 should be implemented as “ $u \leftarrow u.parent$ ” to work with our BFS.

4.1. Example

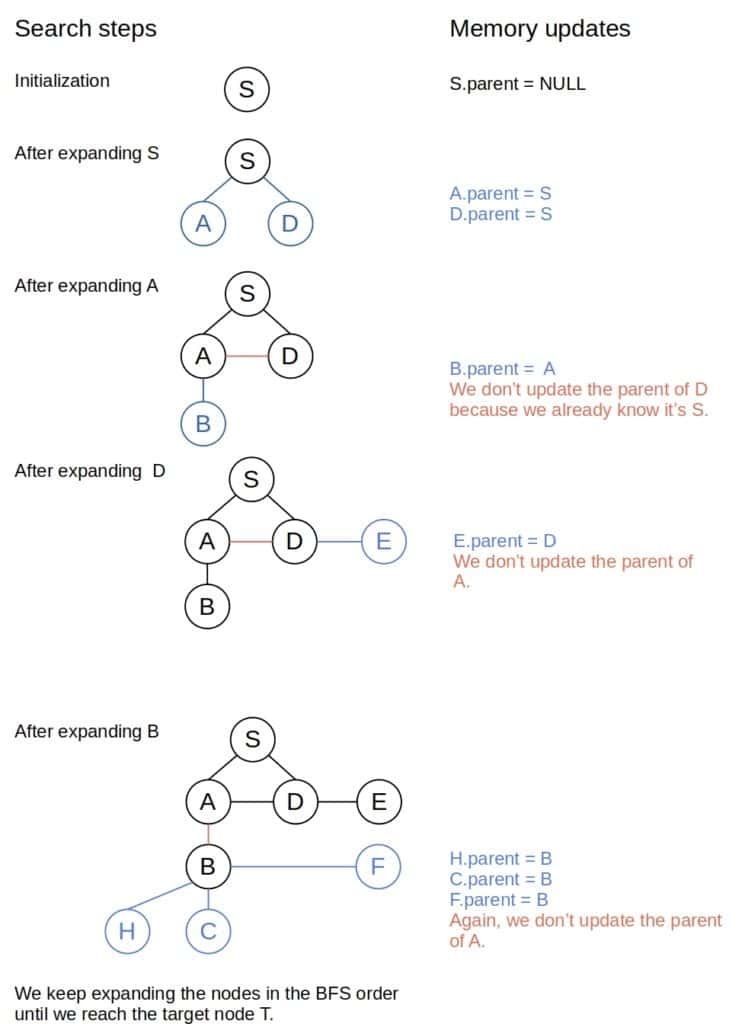
This is how BFS would find the path from $S$ to $T$ in our example:

5. Tracing the Path in Dijkstra’s Algorithm

Unlike DFS and BFS, Dijkstra’s Algorithm (DA) finds the lengths of the shortest paths from the start node to all the other nodes in the graph. Though limited to finite graphs, DA can handle positive-weighted edges in contrast to DFS and BFS.

We apply the same idea with the memory as before and adapt it to DA. The algorithm will update the memory as soon as it updates the currently known length of the shortest path between a node in the graph and the start node. The array $prev$ plays the role of the memory in the pseudocode of DA with path tracing:

Using $prev$ , we can reconstruct the path between $s$ and any node $t$ :

As we see, it’s the same strategy we used in DFS.

6. Conclusion

In this article, we showed several ways to trace the paths in Depth-First Search, Breadth-First Search, and Dijkstra’s Algorithm.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex