1. Introduction
In this tutorial, we’ll study deterministic and stochastic optimization methods. We’ll focus on understanding the similarities and differences of these categories of optimization methods and describe scenarios where they are typically employed.
First, we’ll have a brief review of optimization methods. So, we’ll particularly explore the categories of deterministic and stochastic optimization methods, showing examples of algorithms for each. At last, we’ll compare both categories of optimization methods in a systematic summary.
2. Optimization in Computing
Computer Science is applicable to solve problems and improve processes in multiple areas of knowledge. We can do that by modeling problems and their inputs in a standard way, thus processing them with the proper problem-solving algorithm.
A typical use of problem-solving algorithms is to get optimized solutions for complex problems. As this brief explanation suggests, we call these algorithms of optimization algorithms.
In our context, optimization means the attempt to find an optimal solution to a problem.
However, a single problem usually has several potential solutions. In such a way, optimization algorithms evaluate objective functions to define which candidate solution is the best one.
The adopted objective function, in turn, changes according to the characteristics and constraints of the considered problem.
Moreover, it is not always guaranteed that an optimization algorithm finds the global optima result. Some optimization methods are exact. These always find global optima results. But, we also have non-exact optimization algorithms that may find the global optima result or only local optima ones.
At last, it is relevant to highlight that there is no globally best optimization algorithm. Choosing an optimization algorithm depends, among other aspects, on the problem characteristics, the admissible execution time and available computational resources, and the necessity of finding the global optima solution.
In the following sections, we’ll explore two categories of optimization algorithms: deterministic and stochastic.
3. Deterministic Optimization Algorithms
Deterministic optimization aims to find the global best result, providing theoretical guarantees that the returned result is the global best one indeed. To do that, deterministic optimization algorithms exploit particular and convenient features of a given problem.
Thus, deterministic optimization refers to complete or rigorous classes of algorithms in Neumaier’s classification:
- Complete: algorithms that reach global best results with an indefinitely long execution time. But, it is possible to evaluate and find a sufficient local best result in a finite time considering predefined tolerances
- Rigorous: algorithms that find global best results in a finite execution time and considering predefined tolerances
Deterministic optimization is particularly good for solving problems with clear exploitable features that help to compute the globally optimal result.
However, deterministic algorithms may have problems tackling black-box problems or extremely complex and volatile optimization functions. It occurs due to big searching spaces and the existence of intricate problem structures.
3.1. Examples of Deterministic Optimization Models
We have several classic algorithm models for implementing deterministic optimization algorithms. We briefly discuss some of them next.
The very first model of deterministic optimization is Linear Programming (LP). Linear programming consists of a mathematical model where a problem and its requirements are modeled through linear relationships and evaluated through linear objective functions.
On the other hand, we also have the Nonlinear Programming (NLP) model. In such a case, the problem, constraints, and objective functions may include nonlinear relationships. These problems are very challenging in the context of deterministic optimization.
Both LP and NLP are appropriate to solve convex problems (with a single optimal solution, which is the globally optimal one). But, we do also have options for non-convex optimization problems (with many candidates for optimal results).
Examples of other models of deterministic optimization are Integer Programming (IP), Non-convex Nonlinear Programming (NNLP), and Mixed-Integer Nonlinear Programming (MINLP).
The following image summarizes the deterministic optimization programming models according to the optimization problem features:
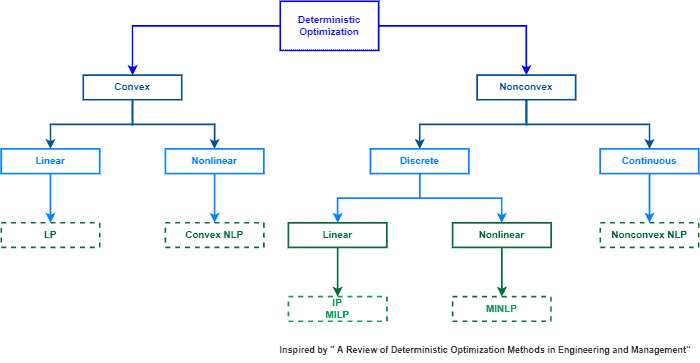
Examples of methods that implement deterministic optimization for these models are branch-and-bound, cutting plane, outer approximation, and interval analysis, among others.
4. Stochastic Optimization Algorithms
Stochastic optimization aims to reach proper solutions to multiple problems, similar to deterministic optimization. However, different from deterministic optimization, stochastic optimization algorithms employ processes with random factors to do so.
Due to these processes with random factors, stochastic optimization does not guarantee finding the optimal result for a given problem. But, there is always a probability of finding the globally optimal result.
Specifically, the probability of finding the globally optimal result in stochastic optimization relates to the available computing time. The probability of finding the globally optimal result increases as the execution time increases. So, if the execution time is infinite, we have a 100% chance of finding the global optima result.
In this way, it is impossible to have 100% certainty of finding the global optima result with stochastic algorithms in practice.
Despite this fact, there are many scenarios in real-life that a globally optimal result is not required. In such cases, simply reaching a result good enough with feasible time is sufficient. Thus, stochastic optimization can be naturally employed.
So, the most relevant advantage of stochastic optimization compared to deterministic optimization is the possibility of controlling the execution time: we can fastly find a result for a complex problem with a large search space (even if this result is a local optima one).
4.1. Heuristics and Metaheuristics
Several heuristics and metaheuristics use stochastic processes to find optimized results for a given problem.
In short, heuristics are strategies employed to solve a particular problem. Metaheuristics, in turn, are generic strategies adapted to solve multiple problems.
As heuristics depend on the problem, we do not have a generic example of stochastic heuristics algorithms. Metaheuristics, in turn, have many algorithms examples.
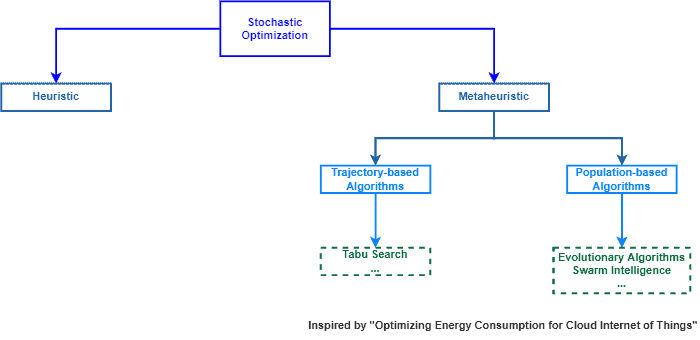
For metaheuristics, we can cite trajectory methods, such as tabu search, that may include stochastic decisions. Furthermore, we have population-based methods, such as genetic algorithms, grey-wolf optimization, and particle swarm optimization, that use several randomized processes.
The image next summarizes stochastic optimization according to its categories of algorithms:
5. Systematic Summary
Several areas of knowledge need to do some kind of optimization to solve particular problems. So, computing provides different optimization algorithms to cover this necessity.
Sometimes, we need to find the optimal result for a problem regardless of the time it takes. In such a case, deterministic optimization algorithms are the best choice.
But, we can have complex problems and a limited time to solve them. Thus, stochastic optimization algorithms are good choices since we can find proper solutions (even the globally optimal ones) in a feasible time.
Of course, deterministic and stochastic optimization include distinct characteristics and algorithms. The following table presents relevant features of deterministic and stochastic optimization.
6. Conclusion
In this article, we studied deterministic and stochastic optimization. First, we reviewed some general concepts regarding optimization in computing. After that, we specifically investigated deterministic and stochastic optimization through relevant characteristics, models, and algorithms. Finally, we compared deterministic and stochastic optimization in a systematic summary.
We can conclude that both deterministic and stochastic algorithms are crucial for solving problems computationally. If the globally optimal result is needed, we do require deterministic optimization. However, stochastic optimization is the best alternative if we only need to find a solution in a given time.