Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
1. Introduction
In this tutorial, we’ll talk about bundle adjustments and their role in photogrammetry and computer vision.
We’ll provide helpful tips and share best practices.
2. The Role in Computer Vision and Photogrammetry
Bundle adjustment (BA) enhances the accuracy and reliability of 3D scene reconstructions from multiple images and camera views:
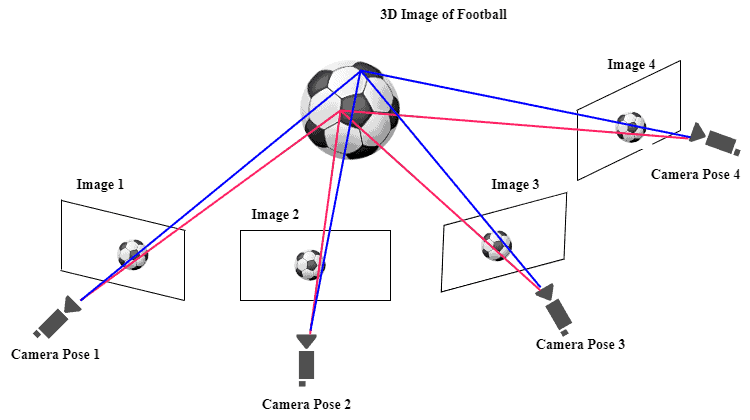
We use it to correct errors from the initial 3D reconstruction process, including inaccuracies in camera pose, scene structure, or feature tracking.
To do so, this technique optimizes the parameters of 3D reconstructions and refines the camera calibration parameters.
2.1. Applications
We use it for object tracking, augmented reality, and scene understanding.
Additionally, it contributes to developing lifelike 3D environments, elevating user immersion and interaction in virtual reality and simulation applications.
3. Workflow and Key Components of Bundle Adjustment
The workflow of Bundle Adjustment (BA) consists of a series of steps designed to refine the parameters of a 3D reconstruction model from several 2D images:
3.1. Data Collection and Initial Reconstruction
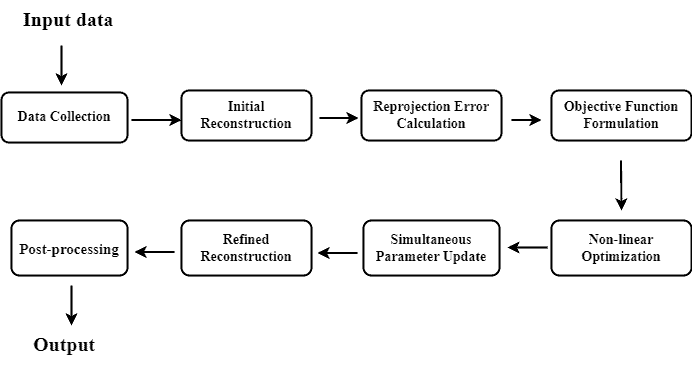
We start with a collection of 2D images capturing the scene or object of interest from different viewpoints, ideally with overlapping features or key points recognizable in multiple images.
To initialize the 3D scene structure and camera parameters, we do an initial structure-from-motion (SfM) estimation. SfM algorithms analyze the image correspondences and camera positions to provide an initial guess of the scene’s 3D structure and camera poses. However, this initial reconstruction often has errors. This is where bundle adjustment comes into play.
3.2. Reprojection Errors and Objective Function Formulation
First, we compute the reprojection errors for each image, measuring the disparity between observed 2D features and their current 3D structure-based projected positions. That way, we asses our 3D model’s accuracy.
We also define an objective function to optimize in further steps. Usually, it’s the sum of squared (reprojection) errors across all images. It quantifies the overall error in the current reconstruction.
3.3. Nonlinear Optimization and Simultaneous Parameter Updates
Nonlinear optimization techniques like Levenberg-Marquardt or Gauss-Newton are used iteratively to minimize the objective function, refining the 3D scene structure and camera parameters.
We apply simultaneous updates to the 3D structure and camera parameters throughout each optimization iteration, ensuring that changes in one reconstruction aspect don’t adversely affect others, thus promoting global consistency.
3.4. Refined Reconstruction and Post-processing
The result of bundle adjustment is a refined 3D reconstruction model with an improved accuracy. This model’s 3D scene structure and camera parameters produce a more precise scene representation.
Subsequently, we undertake post-processing steps, such as mesh generation, texture mapping, or additional filtering, contingent on the particular application requirements.
The outcome is a highly accurate 3D model suitable for various applications, including 3D mapping, computer vision, robotics, and virtual reality.
4. Tools and Software Libraries Used for Bundle Adjustment
There are many tools and software libraries for bundle adjustment:
- OpenCV provides various functions and classes for camera calibration and bundle adjustment, encompassing sparse and dense bundle adjustment. functions
- COLMAP, an open-source software designed for 3D reconstruction from images, incorporates bundle adjustment as an integral part of its pipeline, supporting both sparse and dense reconstruction.
- Bundler, a user-friendly tool for structure-from-motion (SfM), estimates camera parameters and 3D structure from 2D images, making it a suitable choice for basic bundle adjustment tasks.
- g2o, an open-source C++ library specializing in optimizing graph-based nonlinear least-squares problems, enjoys widespread adoption in computer vision and robotics for bundle adjustment purposes.
These tools are implemented in various programming languages and address multiple use cases of bundle adjusting.
However, we can also use a general-purpose optimizer to minimize our objective function, for instance, Scipy and Ceres Solver.
5. Benefits of Using Bundle Adjustment
First, it enhances the accuracy of camera pose estimation and 3D reconstruction.
Furthermore, it ensures internal consistency among all camera poses and 3D points. The alignment of observations across different images reduces errors resulting from individual camera calibrations or noisy measurements.
Moreover, bundle adjustment is robust to outliers and noise in the data. It can effectively handle inaccurate feature correspondences by down-weighting or rejecting outliers during optimization. Feature correspondences identify and align distinct points across images, which is vital for 3D reconstruction. Leaving out outliers or down-weighting inaccurate matches enhances final accuracy, especially when dealing with noise and errors.
Lastly, we can apply this technique to sparse and dense reconstruction scenarios. So. it covers a wide range of applications, from using sparse point clouds in feature tracking to generating dense 3D meshes.
5.1. Summary
By optimizing camera poses and 3D point positions, it corrects errors and inaccuracies, resulting in highly precise and true-to-life 3D models.
Here’s a quick summary of its main benefits:
| Benefits |
|---|
| Improved accuracy |
| Consistency |
| Optimizing parameters |
| Camera calibration |
| Robustness to noisy data |
6. Conclusion
In this article, we discussed bundle adjustment, a method that enhances camera settings and 3D structure estimates in visual applications.
It does so by minimizing the sum of projection errors.