Focal Length and Intrinsic Camera Parameters | Baeldung on Computer Science

1. Overview

In this tutorial, we’ll delve into the concept of focal length and its relationship with the camera intrinsic matrix.

Before explaining these concepts, we’ll review the pinhole camera model, the basic model describing the image formation process.

2. Pinhole Camera Model

The pinhole camera model provides a simplified representation of how light interacts with a camera to form an image. In this model, the camera is represented as a simple box with a tiny hole on one side and a flat image plane on the other. All rays of light are blocked by the walls of the box except those passing through the tiny hole.

When an object is placed in front of the aperture, rays of light emanating from different points of the object pass through the aperture and form an inverted image on the image plane.

The following figure represents the operating principle of the pinhole camera:

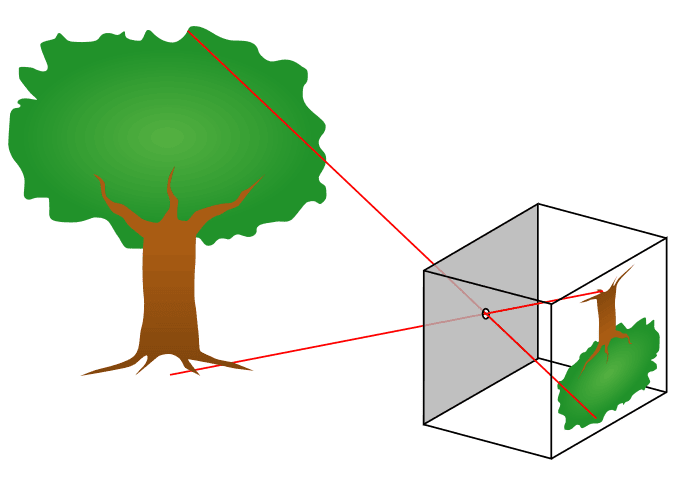
Without the box and the pinhole, the flat image panel would be illuminated from all points in a hemisphere. Hence, uniform coloring is projected on the panel and no image can be observed.

This projection process involves several key factors:

objects farther away from the camera appear smaller in the image
due to the light rays intersecting at a single point (the pinhole), the resulting image on the image plane is inverted
the size of the aperture and its distance from the image plane determines the field of view of the camera. A larger aperture or a shorter distance results in a wider field of view, capturing more of the scene
the image size of the distant object is proportional to the distance from the pinhole aperture to the image panel

However, a real pinhole camera cannot work well because a tiny hole cannot gather enough light in a short exposure time. Hence, lenses are used in cameras to accumulate more light.

2.1. Camera Parameters

Let’s now define the fundamental parameters of the pinhole camera model:

the center of projection is the point where the pinhole aperture is located
the focal length is the distance between the center of the projection and the image plane
the optical axis is the line perpendicular to the image plane and passing through the center of projection
the principal point is defined as the point of intersection between the optical axis and the image plane

The projection geometry of the pinhole camera and the parameters defined above are represented in the following figure:

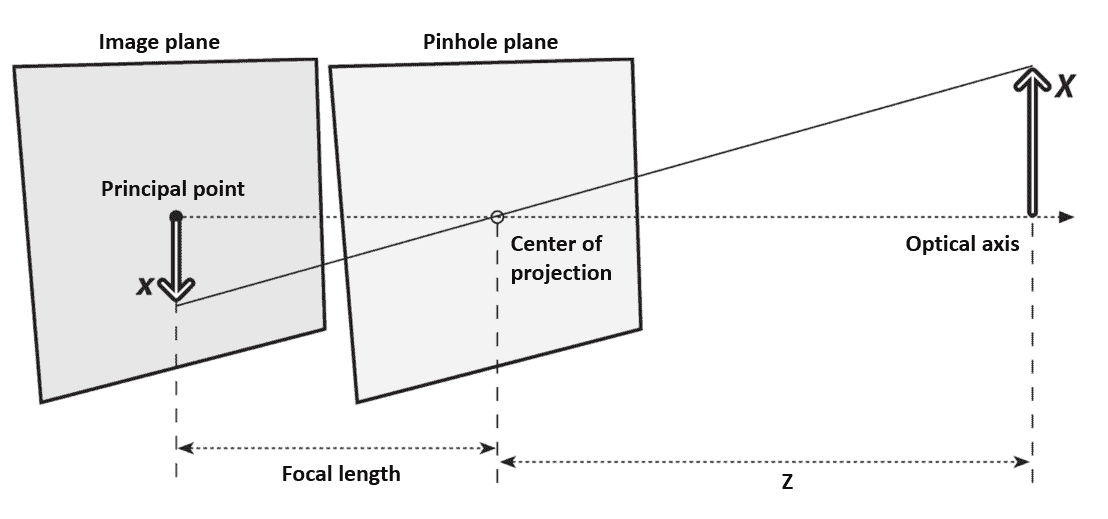
We observe two similar triangles, hence we can derive a simple equation that relates the size of the object and its projected image:

(1) $\begin{equation*} -x = f {X \over Z} \end{equation*}$

where $X$ is the real size of the object, $x$ is the size of the object on the image plane, $f$ is the focal length and $Z$ is the distance from the object to the pinhole aperture. The minus sign is because the image is inverted. Hence, it is more customary to ideally swap the pinhole and the image plane, as shown in the following figure:

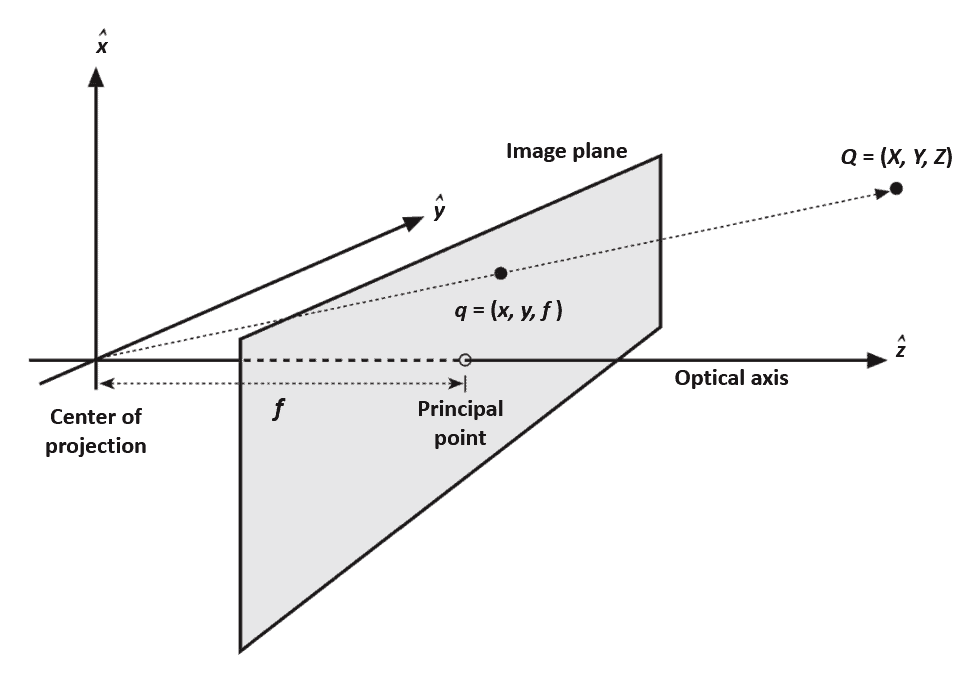
The image plane is ideally placed in front of the pinhole. A point in space $Q = (X, Y, Z)$ is projected on the image plane by tracing the line passing through the point $Q$ and the center of projection. The resulting projection of $Q$ is $q = (x,y,f)$ . In this abstraction, the object appears right side up and the math comes out easier.

3. Understanding Focal Length

The focal length determines the field of view and the magnification of the camera. A longer focal length results in a narrower field of view and magnifies distant objects, while a shorter focal length captures a wider field of view but diminishes the magnification of distant objects.

The relation between a point $Q=(X, Y, Z)$ in the real space and its projection on the image plane at the pixel location $(x_s, y_s)$ is represented by the following equations:

(2) $\begin{equation*} x_s=f_x \frac{X}{Z}+c_x \end{equation*}$

(3) $\begin{equation*} y_s=f_y \frac{Y}{Z}+c_y \end{equation*}$

where $c_x$ and $c_y$ are two parameters that handle possible misalignment of the principal point with the center of the image; $f_x$ and $f_y$ are essentially the focal lengths expressed in pixels. We introduce two new parameters because each pixel on a typical imager is rectangular, hence the pixel lengths in $\mathbf{x}$ and $\mathbf{y}$ are different. It is worth noting that $x_s$ , $y_s$ , $c_x$ , $c_y$ , $f_x$ , $f_y$ are expressed in units of pixels.

The physical focal length $f$ , expressed in units of millimeters, cannot be measured directly. However, the focal lengths $f_x$ and $f_y$ can be measured using a procedure called camera calibration.

4. Camera Intrinsic Matrix

Projective transform is the function that maps the points in the space with coordinates $\mathbf{(X, Y, Z)}$ to its projection $\mathbf{(x_s, y_s)}$ on the image plane. It is customary to express such transform using the homogeneous coordinates, hence the equation (2) and (3) can be written in the following matrix form:

(4) $\begin{equation*} \vec{q}=M \vec{Q} \end{equation*}$

where $\vec{q}$ and $\vec{Q}$ are the coordinates of the point in the space and the corresponding projection coordinates:

(5) $\begin{equation*} \vec{q}=\left[\begin{array}{l} x \\ y \\ w \end{array}\right] \text {and} \vec{Q}=\left[\begin{array}{c} X \\ Y \\ Z \end{array}\right] \end{equation*}$

and M is a 3×3 matrix called camera intrinsic matrix:

(6) $\begin{equation*} M=\left[\begin{array}{ccc} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{array}\right] . \end{equation*}$

The camera intrinsic matrix represents the internal parameters of a camera, including the focal length, and it allows to project 3D points in the world onto the 2D image plane.

The parameters of the camera intrinsic matrix are estimated by performing the camera calibration procedure. The latter is typically performed using a set of known geometric patterns (e.g., chessboard patterns) or objects with precisely measured dimensions, allowing for the estimation of the camera parameters through mathematical algorithms, such as Zhang’s method or the Direct Linear Transform (DLT) algorithm.

5. Conclusion

In this article, we reviewed the focal length and the camera intrinsic parameters, fundamental properties of cameras. Furthermore, we described the image formation process by illustrating the pinhole camera model.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex