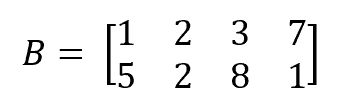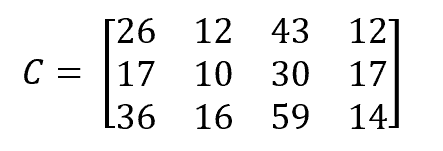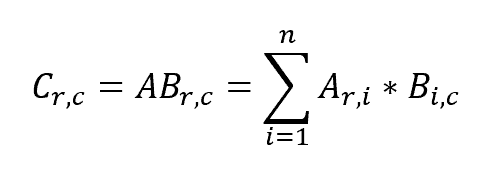1. Overview
In this tutorial, we’ll have a look at how we can multiply two matrices in Java.
As the matrix concept doesn’t exist natively in the language, we’ll implement it ourselves, and we’ll also work with a few libraries to see how they handle matrices multiplication.
In the end, we’ll do a little benchmarking of the different solutions we explored in order to determinate the fastest one.
2. The Example
Let’s begin by setting up an example we’ll be able to refer to throughout this tutorial.
First, we’ll imagine a 3×2 matrix:

Let’s now imagine a second matrix, two rows by four columns this time:
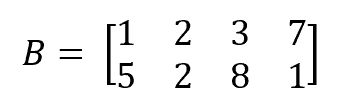
Then, the multiplication of the first matrix by the second matrix, which will result in a 3×4 matrix:
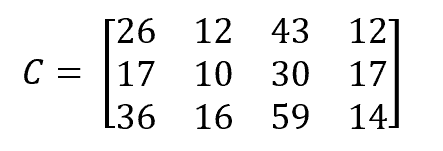
As a reminder, this result is obtained by computing each cell of the resulting matrix with this formula:
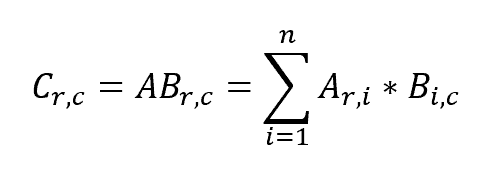
Where r is the number of rows of matrix A, c is the number of columns of matrix B and n is the number of columns of matrix A, which must match the number of rows of matrix B.
3. Matrix Multiplication
3.1. Own Implementation
Let’s start with our own implementation of matrices.
We’ll keep it simple and just use two dimensional double arrays:
double[][] firstMatrix = {
new double[]{1d, 5d},
new double[]{2d, 3d},
new double[]{1d, 7d}
};
double[][] secondMatrix = {
new double[]{1d, 2d, 3d, 7d},
new double[]{5d, 2d, 8d, 1d}
};
Those are the two matrices of our example. Let’s create the one expected as the result of their multiplication:
double[][] expected = {
new double[]{26d, 12d, 43d, 12d},
new double[]{17d, 10d, 30d, 17d},
new double[]{36d, 16d, 59d, 14d}
};
Now that everything is set up, let’s implement the multiplication algorithm. We’ll first create an empty result array and iterate through its cells to store the expected value in each one of them:
double[][] multiplyMatrices(double[][] firstMatrix, double[][] secondMatrix) {
double[][] result = new double[firstMatrix.length][secondMatrix[0].length];
for (int row = 0; row < result.length; row++) {
for (int col = 0; col < result[row].length; col++) {
result[row][col] = multiplyMatricesCell(firstMatrix, secondMatrix, row, col);
}
}
return result;
}
Finally, let’s implement the computation of a single cell. In order to achieve that, we’ll use the formula shown earlier in the presentation of the example:
double multiplyMatricesCell(double[][] firstMatrix, double[][] secondMatrix, int row, int col) {
double cell = 0;
for (int i = 0; i < secondMatrix.length; i++) {
cell += firstMatrix[row][i] * secondMatrix[i][col];
}
return cell;
}
Finally, let’s check that the result of the algorithm matches our expected result:
double[][] actual = multiplyMatrices(firstMatrix, secondMatrix);
assertThat(actual).isEqualTo(expected);
3.2. EJML
The first library we’ll look at is EJML, which stands for Efficient Java Matrix Library. At the time of writing this tutorial, it’s one of the most recently updated Java matrix libraries. Its purpose is to be as efficient as possible regarding calculation and memory usage.
We’ll have to add the dependency to the library in our pom.xml:
<dependency>
<groupId>org.ejml</groupId>
<artifactId>ejml-all</artifactId>
<version>0.38</version>
</dependency>
We’ll use pretty much the same pattern as before: creating two matrices according to our example and check that the result of their multiplication is the one we calculated earlier.
So, let’s create our matrices using EJML. In order to achieve this, we’ll use the SimpleMatrix class offered by the library.
It can take a two dimension double array as input for its constructor:
SimpleMatrix firstMatrix = new SimpleMatrix(
new double[][] {
new double[] {1d, 5d},
new double[] {2d, 3d},
new double[] {1d ,7d}
}
);
SimpleMatrix secondMatrix = new SimpleMatrix(
new double[][] {
new double[] {1d, 2d, 3d, 7d},
new double[] {5d, 2d, 8d, 1d}
}
);
And now, let’s define our expected matrix for the multiplication:
SimpleMatrix expected = new SimpleMatrix(
new double[][] {
new double[] {26d, 12d, 43d, 12d},
new double[] {17d, 10d, 30d, 17d},
new double[] {36d, 16d, 59d, 14d}
}
);
Now that we’re all set up, let’s see how to multiply the two matrices together. The SimpleMatrix class offers a mult() method taking another SimpleMatrix as a parameter and returning the multiplication of the two matrices:
SimpleMatrix actual = firstMatrix.mult(secondMatrix);
Let’s check if the obtained result matches the expected one.
As SimpleMatrix doesn’t override the equals() method, we can’t rely on it to do the verification. But, it offers an alternative: the isIdentical() method which takes not only another matrix parameter but also a double fault tolerance one to ignore small differences due to double precision:
assertThat(actual).matches(m -> m.isIdentical(expected, 0d));
That concludes matrices multiplication with the EJML library. Let’s see what the other ones are offering.
3.3. ND4J
Let’s now try the ND4J Library. ND4J is a computation library and is part of the deeplearning4j project. Among other things, ND4J offers matrix computation features.
First of all, we’ve to get the library dependency:
<dependency>
<groupId>org.nd4j</groupId>
<artifactId>nd4j-native</artifactId>
<version>1.0.0-beta4</version>
</dependency>
Note that we’re using the beta version here because there seems to have some bugs with GA release.
For the sake of brevity, we won’t rewrite the two dimensions double arrays and just focus on how they are used with each library. Thus, with ND4J, we must create an INDArray. In order to do that, we’ll call the Nd4j.create() factory method and pass it a double array representing our matrix:
INDArray matrix = Nd4j.create(/* a two dimensions double array */);
As in the previous section, we’ll create three matrices: the two we’re going to multiply together and the one being the expected result.
After that, we want to actually do the multiplication between the first two matrices using the INDArray.mmul() method:
INDArray actual = firstMatrix.mmul(secondMatrix);
Then, we check again that the actual result matches the expected one. This time we can rely on an equality check:
assertThat(actual).isEqualTo(expected);
This demonstrates how the ND4J library can be used to do matrix calculations.
3.4. Apache Commons
Let’s now talk about the Apache Commons Math3 module, which provides us with mathematic computations including matrices manipulations.
Again, we’ll have to specify the dependency in our pom.xml:
<dependency>
<groupId>org.apache.commons</groupId>
<artifactId>commons-math3</artifactId>
<version>3.6.1</version>
</dependency>
Once set up, we can use the RealMatrix interface and its Array2DRowRealMatrix implementation to create our usual matrices. The constructor of the implementation class takes a two-dimensional double array as its parameter:
RealMatrix matrix = new Array2DRowRealMatrix(/* a two dimensions double array */);
As for matrices multiplication, the RealMatrix interface offers a multiply() method taking another RealMatrix parameter:
RealMatrix actual = firstMatrix.multiply(secondMatrix);
We can finally verify that the result is equal to what we’re expecting:
assertThat(actual).isEqualTo(expected);
Let’s see the next library!
3.5. LA4J
This one’s named LA4J, which stands for Linear Algebra for Java.
Let’s add the dependency for this one as well:
<dependency>
<groupId>org.la4j</groupId>
<artifactId>la4j</artifactId>
<version>0.6.0</version>
</dependency>
Now, LA4J works pretty much like the other libraries. It offers a Matrix interface with a Basic2DMatrix implementation that takes a two-dimensional double array as input:
Matrix matrix = new Basic2DMatrix(/* a two dimensions double array */);
As in the Apache Commons Math3 module, the multiplication method is multiply() and takes another Matrix as its parameter:
Matrix actual = firstMatrix.multiply(secondMatrix);
Once again, we can check that the result matches our expectations:
assertThat(actual).isEqualTo(expected);
Let’s now have a look at our last library: Colt.
3.6. Colt
Colt is a library developed by CERN. It provides features enabling high performance scientific and technical computing.
As with the previous libraries, we must get the right dependency:
<dependency>
<groupId>colt</groupId>
<artifactId>colt</artifactId>
<version>1.2.0</version>
</dependency>
In order to create matrices with Colt, we must make use of the DoubleFactory2D class. It comes with three factory instances: dense, sparse and rowCompressed. Each is optimized to create the matching kind of matrix.
For our purpose, we’ll use the dense instance. This time, the method to call is make() and it takes a two-dimensional double array again, producing a DoubleMatrix2D object:
DoubleMatrix2D matrix = doubleFactory2D.make(/* a two dimensions double array */);
Once our matrices are instantiated, we’ll want to multiply them. This time, there’s no method on the matrix object to do that. We’ve got to create an instance of the Algebra class which has a mult() method taking two matrices for parameters:
Algebra algebra = new Algebra();
DoubleMatrix2D actual = algebra.mult(firstMatrix, secondMatrix);
Then, we can compare the actual result to the expected one:
assertThat(actual).isEqualTo(expected);
4. Benchmarking
Now that we’re done with exploring the different possibilities of matrix multiplication, let’s check which are the most performant.
4.1. Small Matrices
Let’s begin with small matrices. Here, a 3×2 and a 2×4 matrices.
In order to implement the performance test, we’ll use the JMH benchmarking library. Let’s configure a benchmarking class with the following options:
public static void main(String[] args) throws Exception {
Options opt = new OptionsBuilder()
.include(MatrixMultiplicationBenchmarking.class.getSimpleName())
.mode(Mode.AverageTime)
.forks(2)
.warmupIterations(5)
.measurementIterations(10)
.timeUnit(TimeUnit.MICROSECONDS)
.build();
new Runner(opt).run();
}
This way, JMH will make two full runs for each method annotated with @Benchmark, each with five warmup iterations (not taken into the average computation) and ten measurement ones. As for the measurements, it’ll gather the average time of execution of the different libraries, in microseconds.
We then have to create a state object containing our arrays:
@State(Scope.Benchmark)
public class MatrixProvider {
private double[][] firstMatrix;
private double[][] secondMatrix;
public MatrixProvider() {
firstMatrix =
new double[][] {
new double[] {1d, 5d},
new double[] {2d, 3d},
new double[] {1d ,7d}
};
secondMatrix =
new double[][] {
new double[] {1d, 2d, 3d, 7d},
new double[] {5d, 2d, 8d, 1d}
};
}
}
That way, we make sure arrays initialization is not part of the benchmarking. After that, we still have to create methods that do the matrices multiplication, using the MatrixProvider object as the data source. We won’t repeat the code here as we saw each library earlier.
Finally, we’ll run the benchmarking process using our main method. This gives us the following result:
Benchmark Mode Cnt Score Error Units
MatrixMultiplicationBenchmarking.apacheCommonsMatrixMultiplication avgt 20 1,008 ± 0,032 us/op
MatrixMultiplicationBenchmarking.coltMatrixMultiplication avgt 20 0,219 ± 0,014 us/op
MatrixMultiplicationBenchmarking.ejmlMatrixMultiplication avgt 20 0,226 ± 0,013 us/op
MatrixMultiplicationBenchmarking.homemadeMatrixMultiplication avgt 20 0,389 ± 0,045 us/op
MatrixMultiplicationBenchmarking.la4jMatrixMultiplication avgt 20 0,427 ± 0,016 us/op
MatrixMultiplicationBenchmarking.nd4jMatrixMultiplication avgt 20 12,670 ± 2,582 us/op
As we can see, EJML and Colt are performing really well with about a fifth of a microsecond per operation, where ND4j is less performant with a bit more than ten microseconds per operation. The other libraries have performances situated in between.
Also, it’s worth noting that when increasing the number of warmup iterations from 5 to 10, performance is increasing for all the libraries.
4.2. Large Matrices
Now, what happens if we take larger matrices, like 3000×3000? To check what happens, let’s first create another state class providing generated matrices of that size:
@State(Scope.Benchmark)
public class BigMatrixProvider {
private double[][] firstMatrix;
private double[][] secondMatrix;
public BigMatrixProvider() {}
@Setup
public void setup(BenchmarkParams parameters) {
firstMatrix = createMatrix();
secondMatrix = createMatrix();
}
private double[][] createMatrix() {
Random random = new Random();
double[][] result = new double[3000][3000];
for (int row = 0; row < result.length; row++) {
for (int col = 0; col < result[row].length; col++) {
result[row][col] = random.nextDouble();
}
}
return result;
}
}
As we can see, we’ll create 3000×3000 two-dimensions double arrays filled with random real numbers.
Let’s now create the benchmarking class:
public class BigMatrixMultiplicationBenchmarking {
public static void main(String[] args) throws Exception {
Map<String, String> parameters = parseParameters(args);
ChainedOptionsBuilder builder = new OptionsBuilder()
.include(BigMatrixMultiplicationBenchmarking.class.getSimpleName())
.mode(Mode.AverageTime)
.forks(2)
.warmupIterations(10)
.measurementIterations(10)
.timeUnit(TimeUnit.SECONDS);
new Runner(builder.build()).run();
}
@Benchmark
public Object homemadeMatrixMultiplication(BigMatrixProvider matrixProvider) {
return HomemadeMatrix
.multiplyMatrices(matrixProvider.getFirstMatrix(), matrixProvider.getSecondMatrix());
}
@Benchmark
public Object ejmlMatrixMultiplication(BigMatrixProvider matrixProvider) {
SimpleMatrix firstMatrix = new SimpleMatrix(matrixProvider.getFirstMatrix());
SimpleMatrix secondMatrix = new SimpleMatrix(matrixProvider.getSecondMatrix());
return firstMatrix.mult(secondMatrix);
}
@Benchmark
public Object apacheCommonsMatrixMultiplication(BigMatrixProvider matrixProvider) {
RealMatrix firstMatrix = new Array2DRowRealMatrix(matrixProvider.getFirstMatrix());
RealMatrix secondMatrix = new Array2DRowRealMatrix(matrixProvider.getSecondMatrix());
return firstMatrix.multiply(secondMatrix);
}
@Benchmark
public Object la4jMatrixMultiplication(BigMatrixProvider matrixProvider) {
Matrix firstMatrix = new Basic2DMatrix(matrixProvider.getFirstMatrix());
Matrix secondMatrix = new Basic2DMatrix(matrixProvider.getSecondMatrix());
return firstMatrix.multiply(secondMatrix);
}
@Benchmark
public Object nd4jMatrixMultiplication(BigMatrixProvider matrixProvider) {
INDArray firstMatrix = Nd4j.create(matrixProvider.getFirstMatrix());
INDArray secondMatrix = Nd4j.create(matrixProvider.getSecondMatrix());
return firstMatrix.mmul(secondMatrix);
}
@Benchmark
public Object coltMatrixMultiplication(BigMatrixProvider matrixProvider) {
DoubleFactory2D doubleFactory2D = DoubleFactory2D.dense;
DoubleMatrix2D firstMatrix = doubleFactory2D.make(matrixProvider.getFirstMatrix());
DoubleMatrix2D secondMatrix = doubleFactory2D.make(matrixProvider.getSecondMatrix());
Algebra algebra = new Algebra();
return algebra.mult(firstMatrix, secondMatrix);
}
}
When we run this benchmarking, we obtain completely different results:
Benchmark Mode Cnt Score Error Units
BigMatrixMultiplicationBenchmarking.apacheCommonsMatrixMultiplication avgt 20 511.140 ± 13.535 s/op
BigMatrixMultiplicationBenchmarking.coltMatrixMultiplication avgt 20 197.914 ± 2.453 s/op
BigMatrixMultiplicationBenchmarking.ejmlMatrixMultiplication avgt 20 25.830 ± 0.059 s/op
BigMatrixMultiplicationBenchmarking.homemadeMatrixMultiplication avgt 20 497.493 ± 2.121 s/op
BigMatrixMultiplicationBenchmarking.la4jMatrixMultiplication avgt 20 35.523 ± 0.102 s/op
BigMatrixMultiplicationBenchmarking.nd4jMatrixMultiplication avgt 20 0.548 ± 0.006 s/op
As we can see, the homemade implementations and the Apache library are now way worse than before, taking nearly 10 minutes to perform the multiplication of the two matrices.
Colt is taking a bit more than 3 minutes, which is better but still very long. EJML and LA4J are performing pretty well as they run in nearly 30 seconds. But, it’s ND4J which wins this benchmarking performing in under a second on a CPU backend.
4.3. Analysis
That shows us that the benchmarking results really depend on the matrices’ characteristics and therefore it’s tricky to point out a single winner.
5. Conclusion
In this article, we’ve learned how to multiply matrices in Java, either by ourselves or with external libraries. After exploring all solutions, we did a benchmark of all of them and saw that, except for ND4J, they all performed pretty well on small matrices. On the other hand, on larger matrices, ND4J is taking the lead.
The code backing this article is available on GitHub. Once you're
logged in as a Baeldung Pro Member, start learning and coding on the project.