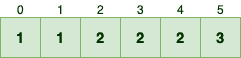1. Overview
General-purpose sorting algorithms like Merge Sort make no assumption about the input, so they can’t beat the O(n log n) in the worst case. Counting Sort, on the contrary, has an assumption about the input which makes it a linear time sorting algorithm.
In this tutorial, we’re going to get acquainted with the mechanics of the Counting Sort and then implement it in Java.
2. Counting Sort
Counting sort, as opposed to most classic sorting algorithms, does not sort the given input by comparing the elements. Instead, it assumes that the input elements are n integers in the range [0, k]. When k = O(n), then the counting sort will run in O(n) time.
Please note, then, that we can’t use the counting sort as a general-purpose sorting algorithm. However, when the input is aligned with this assumption, it’s pretty fast!
2.1. Frequency Array
Let’s suppose we’re going to sort an input array with values in the [0, 5] range:

First, we should count the occurrence of each number in the input array. If we represent the countings with array C, then C[i] represents the frequency of number i in the input array:
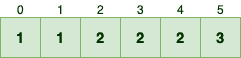
For example, since 5 appears 3 times in the input array, the value for the index 5 is equal to 3.
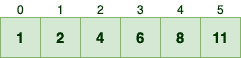
Now given the array C, we should determine how many elements are less than or equal to each input element. For example:
- One element is less than or equal to zero, or in other words, there is only one zero value, which is equal to C[0]
- Two elements are less than or equal to one, which is equal to C[0] + C[1]
- Four values are less than or equal to two, which is equal to C[0] + C[1] + C[2]
So if we keep computing the summation of n consecutive elements in C, we can know how many elements are less than or equal to number n-1 in the input array. Anyway, by applying this simple formula we can update the C as the following:
2.2. The Algorithm
Now we can use the auxiliary array C to sort the input array. Here’s how the counting sort works:
- It iterates the input array in reverse
- For each element i, C[i] – 1 represents the location of number i in the sorted array. This is because of the fact that there are C[i] elements less than or equal to i
- Then, it decrements the C[i] at the end of each round
In order to sort the sample input array, we should first start with the number 5, since it’s the last element. According to C[5], there are 11 elements are less than or equal to the number 5.
So, 5 should be the 11th element in the sorted array, hence the index 10:
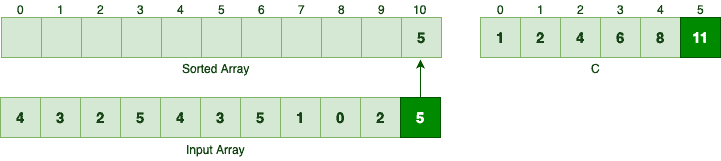
Since we moved 5 to the sorted array, we should decrement the C[5]. Next element in the reversed order is 2. Since there are 4 elements less than or equal to 2, this number should be the 4th element in the sorted array:
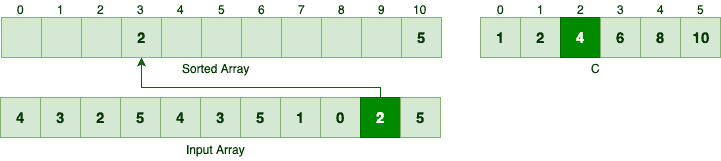
Similarly, we can find the right spot for the next element which is 0:
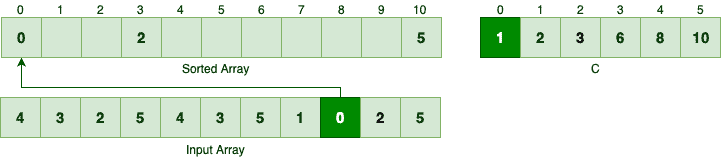
If we keep iterating in reverse and move each element appropriately, we would end up with something like:

3. Counting Sort – Java Implementation
3.1. Computing the Frequency Array
First off, given an input array of elements and the k, we should compute the array C:
int[] countElements(int[] input, int k) {
int[] c = new int[k + 1];
Arrays.fill(c, 0);
for (int i : input) {
c[i] += 1;
}
for (int i = 1; i < c.length; i++) {
c[i] += c[i - 1];
}
return c;
}
Let’s breakdown the method signature:
- input represents an array of numbers we’re going to sort
- The input array is an array of integers in the range of [0, k] – so k represents the maximum number in the input
- The return type is an array of integers representing the C array
And here’s how the countElements method works:
- First, we initialized the C array. As the [0, k] range contains k+1 numbers, we’re creating an array capable of containing k+1 numbers
- Then for each number in the input, we’re computing the frequency of that number
- And finally, we’re adding consecutive elements together to know how many elements are less than or equal to a particular number
Also, we can verify that the countElements method works as expected:
@Test
void countElements_GivenAnArray_ShouldCalculateTheFrequencyArrayAsExpected() {
int k = 5;
int[] input = { 4, 3, 2, 5, 4, 3, 5, 1, 0, 2, 5 };
int[] c = CountingSort.countElements(input, k);
int[] expected = { 1, 2, 4, 6, 8, 11 };
assertArrayEquals(expected, c);
}
Now that we can calculate the frequency array, we should be able to sort any given set of numbers:
int[] sort(int[] input, int k) {
int[] c = countElements(input, k);
int[] sorted = new int[input.length];
for (int i = input.length - 1; i >= 0; i--) {
int current = input[i];
sorted[c[current] - 1] = current;
c[current] -= 1;
}
return sorted;
}
Here’s how the sort method works:
- First, it computes the C array
- Then, it iterates the input array in reverse and for each element in the input, finds its correct spot in the sorted array. The ith element in the input should be the C[i]th element in the sorted array. Since Java arrays are zero-indexed, the C[i]-1 entry is the C[i]th element – for example, sorted[5] is the sixth element in the sorted array
- Each time we find a match, it decrements the corresponding C[i] value
Similarly, we can verify that the sort method works as expected:
@Test
void sort_GivenAnArray_ShouldSortTheInputAsExpected() {
int k = 5;
int[] input = { 4, 3, 2, 5, 4, 3, 5, 1, 0, 2, 5 };
int[] sorted = CountingSort.sort(input, k);
// Our sorting algorithm and Java's should return the same result
Arrays.sort(input);
assertArrayEquals(input, sorted);
}
4. Revisiting the Counting Sort Algorithm
4.1. Complexity Analysis
Most classic sorting algorithms, like merge sort, sort any given input by just comparing the input elements to each other. These type of sorting algorithms are known as comparison sorts. In the worst case, comparison sorts should take at least O(n log n) to sort n elements.
Counting Sort, on the other hand, does not sort the input by comparing the input elements, so it’s clearly not a comparison sort algorithm.
Let’s see how much time it consumes to sort the input:
- It computes the C array in O(n+k) time: It once iterates an input array with size n in O(n) and then iterates the C in O(k) – so that would be O(n+k) in total
- After computing the C, it sorts the input by iterating the input array and performing a few primitive operations in each iteration. So, the actual sort operation takes O(n)
In total, counting sort takes O(n+k) time to run:
O(n + k) + O(n) = O(2n + k) = O(n + k)
If we assume k=O(n), then counting sort algorithm sorts the input in linear time. As opposed to general-purpose sorting algorithms, counting sorts makes an assumption about the input and takes less than the O(n log n) lower bound to execute.
4.2. Stability
A few moments ago, we laid a few peculiar rules about the mechanics of counting sort but never cleared the reason behind them. To be more specific:
- Why should we iterate the input array in reverse?
- Why we decrement the C[i] each time we’re using it?
Let’s iterate from the beginning to better understand the first rule. Suppose we’re going to sort a simple array of integers like the following:
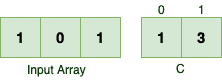
In the first iteration, we should find the sorted location for the first 1:
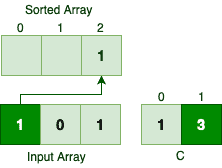
So the first occurrence of number 1 gets the last index in the sorted array. Skipping the number 0, let’s see what happens to the second occurrence of number 1:
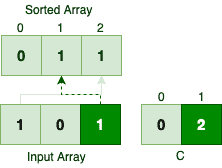
The appearance order of elements with the same value is different in the input and sorted array, so the algorithm is not stable when we’re iterating from the beginning.
What happens if we don’t decrement the C[i] value after each use? Let’s see:
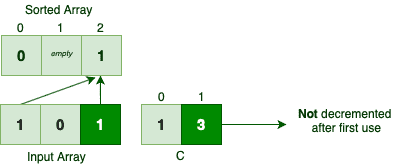
Both occurrences of number 1 are getting the last place in the sorted array. So if we don’t decrement the C[i] value after each use, we could potentially lose a few numbers while sorting them!
5. Conclusion
In this tutorial, first, we learned how the Counting Sort works internally. Then we implemented this sorting algorithm in Java and wrote a few tests to verify its behavior. And finally, we proved that the algorithm is a stable sorting algorithm with linear time complexity.
The code backing this article is available on GitHub. Once you're
logged in as a Baeldung Pro Member, start learning and coding on the project.