Check if Two Strings Are Permutations of Each Other in Java

1. Overview

A permutation or anagram is a word or phrase formed by rearranging the letters of a different word or phrase. In other words, a permutation contains the same characters as another string, but the order of the arrangement of the characters can vary.

In this tutorial, we’ll examine solutions to check whether a string is a permutation or anagram of another string.

2. What Is a String Permutation?

Let’s look at a permutation example and see how to start thinking about a solution.

2.1. Permutation

Let’s look at the permutations of the word CAT:

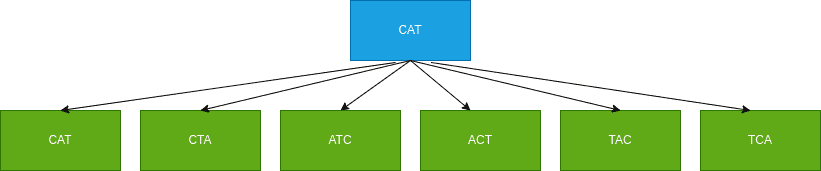
Notably, there are six permutations (including CAT itself). We can count n! (factorial of n) where n is the string’s length.

2.2. How to Approach a Solution

As we can see, there are many possible permutations of a string. We might think of creating an algorithm that loops over all the string’s permutations to check whether one is equal to the string we’re comparing.

That works, but we must first create all possible permutations, which can be expensive, especially with large strings.

However, we notice that no matter the permutation, it contains the same characters as the original. For example, CAT and TAC have the same characters [A,C,T], even if in a different sequence.

Therefore, we could store the characters of the strings in a data structure and then find a way to compare them.

Notably, we can say that two strings aren’t permutations if they have different lengths.

3. Sorting

The most straightforward approach to solving this problem is sorting and comparing the two strings.

Let’s look at the algorithm:

boolean isPermutationWithSorting(String s1, String s2) {
    if (s1.length() != s2.length()) {
        return false;
    }
    char[] s1CharArray = s1.toCharArray();
    char[] s2CharArray = s2.toCharArray();
    Arrays.sort(s1CharArray);
    Arrays.sort(s2CharArray);
    return Arrays.equals(s1CharArray, s2CharArray);
}

Notably, a string is an array of primitive characters. Therefore, we’ll sort both strings’ character arrays and compare them with the equals() method.

Let’s look at the algorithm complexity:

• Time complexity: O(n log n) for sorting
• Space complexity: O(n) auxiliary space for sorting

We can now look at some tests where we check permutations of a simple word and a sentence:

@Test
void givenTwoStringsArePermutation_whenSortingCharsArray_thenPermutation() {
    assertTrue(isPermutationWithSorting("baeldung", "luaebngd"));
    assertTrue(isPermutationWithSorting("hello world", "world hello"));
}

@Test
void givenTwoStringsAreNotPermutation_whenSortingCharsArray_thenNotPermutation() {
    assertFalse(isPermutationWithSorting("baeldung", "luaebgd"));
    assertFalse(isPermutationWithSorting("baeldung", "luaebngq"));
}

4. Count Frequencies

If we consider our words finite characters, we can use their frequencies in an array of the same dimension. We can consider the 26 letters of our alphabet or the extended ASCII encoding more generically, up to 256 positions in our array.

4.1. Two Counters

We can use two counters, one for each word:

boolean isPermutationWithTwoCounters(String s1, String s2) {
    if (s1.length() != s2.length()) {
        return false;
    }
    int[] counter1 = new int[256];
    int[] counter2 = new int[256];
    for (int i = 0; i < s1.length(); i++) {
        counter1[s1.charAt(i)]++;
    }

    for (int i = 0; i < s2.length(); i++) {
        counter2[s2.charAt(i)]++;
    }

    return Arrays.equals(counter1, counter2);
}

After saving the frequencies in each counter, we can check if the counters are equal.

Let’s look at the algorithm complexity:

• Time complexity: O(n) for accessing the counters
• Space complexity: O(1) constant size of the counters

Next, let’s look at positive and negative test cases:

@Test
void givenTwoStringsArePermutation_whenTwoCountersCharsFrequencies_thenPermutation() {
    assertTrue(isPermutationWithTwoCounters("baeldung", "luaebngd"));
    assertTrue(isPermutationWithTwoCounters("hello world", "world hello"));
}

@Test
void givenTwoStringsAreNotPermutation_whenTwoCountersCharsFrequencies_thenNotPermutation() {
    assertFalse(isPermutationWithTwoCounters("baeldung", "luaebgd"));
    assertFalse(isPermutationWithTwoCounters("baeldung", "luaebngq"));
}

4.2. One Counter

We can be smarter and use only one counter:

boolean isPermutationWithOneCounter(String s1, String s2) {
    if (s1.length() != s2.length()) {
        return false;
    }
    int[] counter = new int[256];
    for (int i = 0; i < s1.length(); i++) {
        counter[s1.charAt(i)]++;
        counter[s2.charAt(i)]--;
    }
    for (int count : counter) {
        if (count != 0) {
            return false;
        }
    }
    return true;
}

We add and remove the frequencies in the same loop using only one counter. Therefore, we finally need to check whether all frequencies equal zero.

Let’s look at the algorithm complexity:

• Time complexity: O(n) for accessing the counter
• Space complexity: O(1) constant size of the counter

Let’s look again at some tests:

@Test
void givenTwoStringsArePermutation_whenOneCounterCharsFrequencies_thenPermutation() {
    assertTrue(isPermutationWithOneCounter("baeldung", "luaebngd"));
    assertTrue(isPermutationWithOneCounter("hello world", "world hello"));
}

@Test
void givenTwoStringsAreNotPermutation_whenOneCounterCharsFrequencies_thenNotPermutation() {
    assertFalse(isPermutationWithOneCounter("baeldung", "luaebgd"));
    assertFalse(isPermutationWithOneCounter("baeldung", "luaebngq"));
}

4.3. Using HashMap

We can use a map instead of an array to count the frequencies. The idea is the same, but using a map allows us to store more characters. This helps with Unicode, including, for instance, East European, African, Asian, or emoji characters.

Let’s look at the algorithm:

boolean isPermutationWithMap(String s1, String s2) {
    if (s1.length() != s2.length()) {
        return false;
    }
    Map<Character, Integer> charsMap = new HashMap<>();

    for (int i = 0; i < s1.length(); i++) {
        charsMap.merge(s1.charAt(i), 1, Integer::sum);
    }

    for (int i = 0; i < s2.length(); i++) {
        if (!charsMap.containsKey(s2.charAt(i)) || charsMap.get(s2.charAt(i)) == 0) {
            return false;
        }
        charsMap.merge(s2.charAt(i), -1, Integer::sum);
    }

    return true;
}

Once we know the frequencies of a string’s characters, we can check whether the other string contains all the required matches.

Notably, while using maps, we don’t compare arrays positionally as in previous examples. Therefore, we already know if either a key in the map doesn’t exist or the frequency value doesn’t correspond.

Let’s look at the algorithm complexity:

• Time complexity: O(n) for accessing the map in constant time
• Space complexity: O(m) where m is the number of characters we store in the map depending on the complexity of the strings

For testing, this time, we can also add non-ASCII characters:

@Test
void givenTwoStringsArePermutation_whenCountCharsFrequenciesWithMap_thenPermutation() {
    assertTrue(isPermutationWithMap("baelduňg", "luaebňgd"));
    assertTrue(isPermutationWithMap("hello world", "world hello"));
}

For the negative cases, to get 100% test coverage, we must consider the case when the map doesn’t contain the key or there is a value mismatch:

@Test
void givenTwoStringsAreNotPermutation_whenCountCharsFrequenciesWithMap_thenNotPermutation() {
    assertFalse(isPermutationWithMap("baelduňg", "luaebgd"));
    assertFalse(isPermutationWithMap("baeldung", "luaebngq"));
    assertFalse(isPermutationWithMap("baeldung", "luaebngg"));
}

5. String That Contains a Permutation

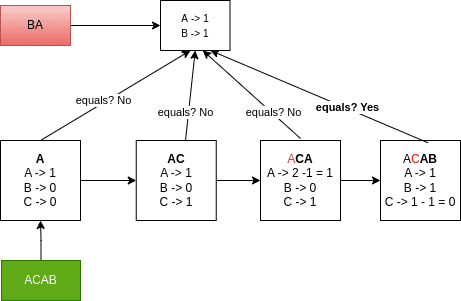
What if we want to check whether a string contains another string as a permutation? For example, we can see that the string acab includes ba as a permutation; ab is a permutation of ba and is included in acab starting at the third character.

We could go through all the permutations discussed earlier, but that wouldn’t be efficient. Counting frequencies wouldn’t work, either. For instance, checking if cb is a permutation inclusion of acab leads to a false positive.

However, we can still use counters as a starting point and then check the permutation using a sliding window technique.

We use a frequency counter for every string. We start by adding to the counter of the potential permutation. Then, we loop on the second string’s characters and follow this pattern:

• add a new succeeding character to the new window considered
• remove one preceding character when exceeding the window length

The window has the length of the potential permutation string. Let’s picture this in a diagram:

Let’s look at the algorithm. s2 is the string for which we want to check the inclusion. Furthermore, we narrow the case to the 26 characters of the alphabet for simplicity:

boolean isPermutationInclusion(String s1, String s2) {
    int ns1 = s1.length(), ns2 = s2.length();
    if (ns1 < ns2) {
        return false;
    }

    int[] s1Count = new int[26];
    int[] s2Count = new int[26];

    for (char ch : s2.toCharArray()) {
        s2Count[ch - 'a']++;
    }

    for (int i = 0; i < ns1; ++i) {
        s1Count[s1.charAt(i) - 'a']++;
        if (i >= ns2) {
            s1Count[s1.charAt(i - ns2) - 'a']--;
        }
        if (Arrays.equals(s1Count, s2Count)) {
            return true;
        }
    }

    return false;
}

Let’s look at the final loop where we apply the sliding window. We add to the frequency counter. However, when the window exceeds the permutation length, we remove an occurrence of the character.

Notably, if the strings have the same length, we fall into the anagram case we have seen earlier.

Let’s look at the algorithm complexity. Let l1 and l2 be the length of the strings s1 and s2:

• Time complexity: O(l1 + 26*(l2 -l1)) depending on the difference between the strings and the character’s range
• Space complexity: O(1) constant space to keep track of the frequencies

Let’s look at some positive test cases where we check both an exact match or a permutation:

@Test
void givenTwoStrings_whenIncludePermutation_thenPermutation() {
    assertTrue(isPermutationInclusion("baeldung", "ea"));
    assertTrue(isPermutationInclusion("baeldung", "ae"));
}

Let’s look at some negative test cases:

@Test
void givenTwoStrings_whenNotIncludePermutation_thenNotPermutation() {
    assertFalse(isPermutationInclusion("baeldung", "au"));
    assertFalse(isPermutationInclusion("baeldung", "baeldunga"));
}

6. Conclusion

In this article, we saw some algorithms for checking whether a string is a permutation of another string. Sorting and comparing the string characters is a straightforward solution. More interestingly, we can achieve linear complexity by storing the character frequencies in counters and comparing them. We can obtain the same result using a map instead of an array of frequencies. Finally, we also saw a variation of the problem by using sliding windows to check whether a string contains a permutation of another string.