Difference Between Tree Order and Degree

1. Overview

In this tutorial, we’ll talk about the difference between order and degree in terms of tree data structure.

First, we’ll define the tree order and provide an example to explain it. Then, we’ll define the tree degree, present an approach to compute it and work through its implementation and time complexity.

2. Tree Order

2.1. Definition

The order of the tree represents the maximum number of children a tree’s node could have. So when we say we have a B-Tree of order , It means every node of that B-Tree can have a maximum of children.

2.2. Examples

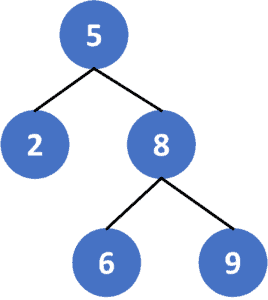
ِA Binary Search Tree is a tree of order 2 since each binary search tree node has at most 2 children:

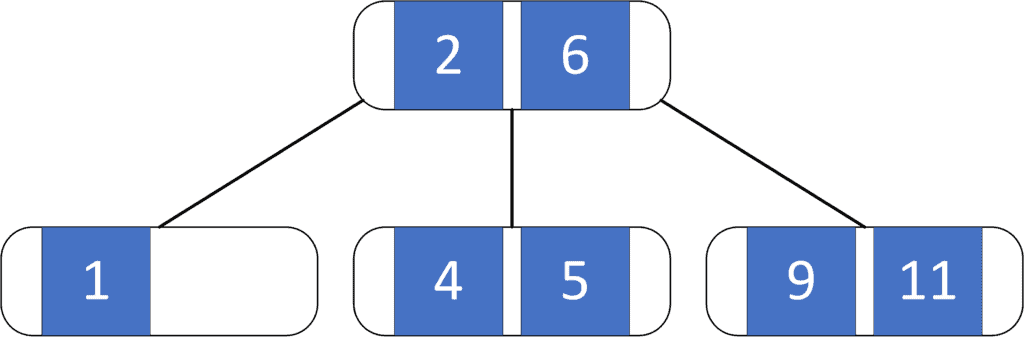
In a B-Tree of order 3, all of its nodes have at most 3 children:

3. Tree Degree

3.1. Definition

The degree of a tree represents the maximum degree of a node in the tree. Recall for a given node, its degree is equal to the number of its children.

Therefore, to get the degree of a tree we’ll use one of the tree traversal methods to iterate over all the nodes of the tree. Then, for each node, we’ll compute its degree which equals the number of children for that node.

Finally, the tree degree is the maximum degree among all the nodes’ degrees.

3.2. Algorithm

Let’s take a look at the implementation of the algorithm:

algorithm ComputeDegree(node, children)
    // INPUT
    //    node = a node in the tree
    //    children = a map associating each node with its children
    // OUTPUT
    //    The maximum degree found in the tree rooted at node
    
    degree <- length(children[node])
    for child in children[node]:
        degree <- MAX(degree, ComputeDegree(child, children))
    return degree

Initially, we have the function that will return the degree of the given tree using DFS traversal. The function will have two parameters. The first one is representing the current node, while the second one is which is the adjacency matrix that stores the given tree.

First, we declare and its initial value equals the degree of the current node which is the size of the list that stores the current node children.

Second, we iterate over the children of the current node, and for each child, we’ll call our function on it, so the function will return the maximum degree in the subtree rooted at . Then, we’ll try to maximize the current with the degree of the subtree.

Finally, will return the degree of the given tree.

3.3. Complexity

The time complexity of the previous approach is , where is the number of nodes in the given tree, and is the number of edges of the tree. The reason behind this complexity is that we only iterate over each node and edge at most once, which is the same as the complexity of DFS traversal.

Since the number of edges in a tree equals , we can say that the complexity is .

4. Conclusion

In this article, we discussed the difference between the order and degree in terms of tree data structure. We defined each of the terms and provided an example to explain it. Finally, we provided an approach to computing the degree of a tree data structure and walked through its implementation and time complexity.