Difference Between a SVM and a Perceptron

Last updated: March 18, 2024

Reviewed by: Grzegorz Piwowarek

1. Introduction

In this tutorial, we’ll briefly introduce support vector machine and perceptron algorithms. Then we’ll explain the differences between them, and how to use them.

The focus will be to discuss all the doubts we may have when it comes to the similarities and differences between these two algorithms.

2. Support Vector Machine

The support vector machine (SVM) method is a popular and effective machine learning method that finds its application in a wide range of different areas. Furthermore, various modifications of this method are still being developed. We can use this method for both the problems of classification and regression, but it’s more common to use it for classification.

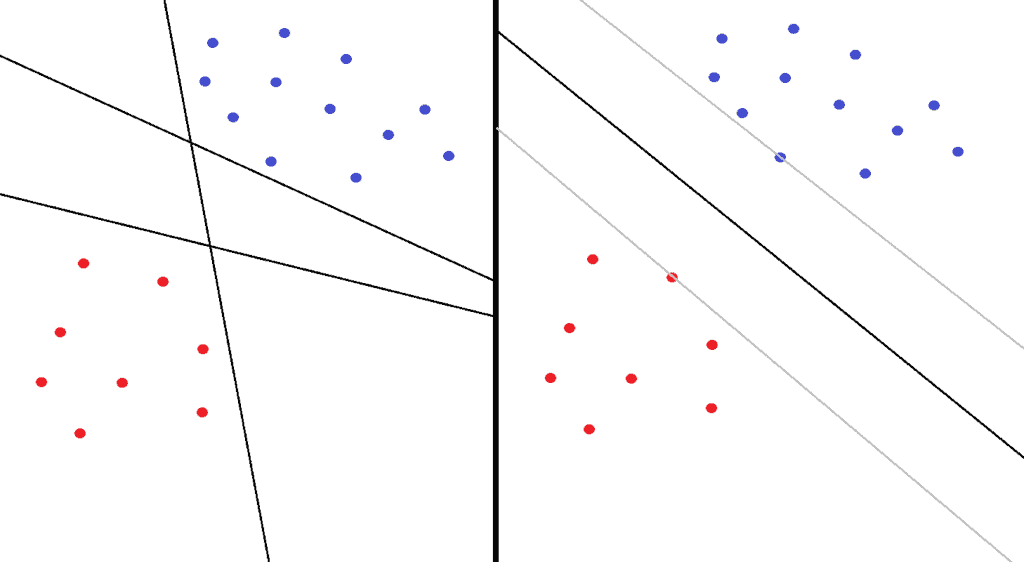
In short, the main idea behind this classification algorithm is to separate classes as correctly as possible. For example, if we take the classification of red and blue dots in the left image below, we can see that all three lines (generally hyperplanes) correctly separate the class of red and blue dots.

However, the question arises as to which is the best solution in general for some other points of these classes as well. The SVM solves this problem by dividing these two classes in such a way that the hyperplane remains as far away as possible from the two nearest points of both classes. We can see this in the right image below.

The maximum possible margin was constructed between these two classes as a space between two parallel gray boundary hyperplanes, while in their midst, there is a hyperplane of separation. These two parallel gray hyperplanes intersect one or more points that we call support vectors:

svm

If we strictly require that all samples lay outside of the margin, then it’s a hard-margin classification. This method is very sensitive to anomalies, such as outliers whose presence is possible. As a result, the model might have a small margin and be too adapted to the data with poor generalization.

Therefore, we introduce soft-margin classification, which is more commonly used in practice. Basically, it allows that a certain number of samples enter the margin, or go to the wrong side of the hyperplane.

3. Perceptron

Perceptron is a supervised machine learning algorithm that solves the problem of binary classification. In short, it works by recognizing patterns from input data to make predictions about target classes. The perceptron is also the first type of artificial neural network.

This algorithm is a type of linear classifier that takes vector x = (x_{1}, x_{2}, ..., x_{n}) as an input, and calculates the linear combination:

(1)   \begin{align*} z = x \cdot w + b \end{align*}

for a weight vector w = (w_{1}, w_{2}, ..., w_{n}) and a bias b. After that, we apply the step function:

(2)   \begin{equation*} h(z) = \begin{cases} 1, & \text{if $z \geq 0$}, \\ 0, & \text{if $z < 0$}. \end{cases} \end{equation*}

Formally, the model that we defined with one neuron and step activation function is perceptron, but there are many other architectures with more layers of neurons and other activation functions. Similar to any neural network, the training and weight update is done by backpropagation as:

(3)   \begin{equation*} w(t+1) = w(t) + \alpha (y_{j} - \hat{y_{j}})x_{j}, \end{equation*}

where w is a weight vector, y_{j} is the real class value, \hat{y_{j}} is the predicted class value, and \alpha is the learning rate.

4. Key Differences

Although these two algorithms are very similar, and they’re solving the same problem, there are major differences between them.

4.1. Inspiration

As we mentioned above, the perceptron is a neural network type of model. The inspiration for creating perceptron came from simulating biological networks. In contrast, SVM is a different type of machine learning model, which was inspired by statistical learning theory.

4.2. Training and Optimization

Generally, for training and optimizing weights of perceptron and neural networks, we use the backpropagation technique, which includes the gradient descent approach. Conversely, to maximize the margin of SVM, we need to solve quadratic equations using quadratic programming (QP).

For example, in the popular machine learning library Scikit-Learn, QP is solved by an algorithm called sequential minimal optimization (SMO).

4.3. Kernel Trick

The SVM algorithm uses one smart technique that we call the kernel trick. The main idea is that when we can’t separate the classes in the current dimension, we add another dimension where the classes may be separable.

In order to do that, we don’t just arbitrarily add another dimension, we use special transformations called kernels.

The most popular kernel functions are:

(4)   \begin{equation*} \begin{split} Linear:\ &K(u, v) = u\cdot v,\\ Polynomial:\ &K(u,v) = (\gamma u\cdot v+c)^d,\\ {Gauss RBF}:\ &K(u,v) = \exp{(-\gamma\|u-v\|^2)},\\ Sigmoid:\ &K(u,v) = \tanh{\gamma u\cdot v+c}. \end{split} \end{equation*}

For example, we can transform two vectors, u and v, from 2D to 3D using the polynomial kernel with parameters d=2, c=0, and \gamma = 1:

(5)   \begin{equation*} \begin{split} K(u, v) &= (u\cdot v)^2 = [(u_{1}, u_{2})\cdot (v_{1}, v_{2})]^2 = (u_{1}v_{1} + u_{2}v_{2})^2 =\\ &= u_{1}^{2}v_{1}^{2} + 2u_{1}v_{1}u_{2}v_{2} + u_{2}^{2}v_{2}^{2}=\\ &= (u_{1}^{2}, \sqrt{2}u_{1}u_{2}, u_{2}^{2})\cdot (v_{1}^{2}, \sqrt{2}v_{1}v_{2}, v_{2}^{2}) = \\ &=\phi(u)\cdot \phi(v). \end{split} \end{equation*}

Lastly, the kernel trick is efficient because we don’t have to explicitly transform samples of data into a higher dimension. This is because we can directly apply the kernel trick K(u, v) in the SVM dual formulation:

(6)   \begin{align*} \max_{\alpha}\quad &F(\alpha) = \sum_{i=1}^{m}\alpha_{i} - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y^{(i)}y^{(j)}K(\textbf{x}^{(i)},\textbf{x}^{(j)})\\ s. t.\quad &\alpha_{i} \geq 0,\ i=1,2,...,m\\ &\sum_{i=1}^{m}\alpha_{i}y^{(i)} = 0. \end{align*}

In contrast to SVM, perceptron doesn’t use the kernel trick and doesn’t transform the data into a higher dimension. Consequently, if the data isn’t easily separable with the current configuration of perceptron, we can try to increase the number of neurons or layers in the model.

4.4. Multiclass Classification

SVM doesn’t support multiclass classification natively. Therefore, if we want to separate multiple classes using SVM algorithms, there are two indirect approaches:

  • One-vs-One approach
  • One-vs-Rest approach

One-vs-One (OvO) approach means that we break the multiclass problem into multiple binary classification problems. For example, if we have three classes with names X, Y, and Z, the OvO approach would divide it into three binary classification problems:

  1.  X vs Y
  2.  X vs Z
  3.  Y vs Z

Similarly, One-vs-Rest (OvR) approach breaks the multiclass problem into multiple binary classifications where it tries to separate the current class with all the other classes together. For example, if we take the same classes as above, the OvR approach looks like this:

  1.  X vs [Y, Z]
  2.  Y vs [X, Z]
  3.  Z vs [X, Z]

Although classic perceptron with one neuron requires the same logic for solving multiclass classification problems, most of today’s implementations of perceptron algorithms can directly predict the probability for each of the classes. This is simply done using the softmax activation function in the output layer.

4.4. Probability of Prediction

Finally, the SVM model doesn’t output probability natively. Therefore, if we want to have a probability of prediction, we can get it indirectly with the probability calibration method. One standard way is using Platt scaling.

In contrast to SVM, perceptron with probabilistic activation function in the output layer directly predicts the probability for each class. The most common probabilistic functions are sigmoid and softmax.

5. Conclusion

In this article, we briefly described two popular machine learning algorithms, SVM and perceptron. We also explained several key differences between them. Finally, we learned how to distinguish between these two methods, and use them based on the situation.

Comments are open for 30 days after publishing a post. For any issues past this date, use the Contact form on the site.