Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: February 12, 2025
The loss function is an integral part of the machine learning process. It provides an informative signal that tells us how well the model performs. In many cases, it also provides a direct learning signal by taking its derivative concerning model parameters. This is the case for neural networks. Since the loss function tells us how to update our model, it is important to choose the right one, and this may not always be the most obvious loss.
In this tutorial, we introduce the concept of surrogate loss functions and show how they can be used to provide an informative learning signal.
A loss function quantifies how well or poorly an approximation of a function approximates its actual value. In the case of classification, we usually want to approximate a function such that we minimize the empirical risk of incorrect classification.
An example is that of binary classification. We have a dataset composed of vector, observations
, and labels
where
is an element of the set
.
We have a model . This relatively simple model predicts the positive class for values
and the negative class otherwise. In order to optimize this model, we need to discover the optimal weights
. To discover the optimal weights, we need to evaluate
and compute the loss.
In this case, a classic and natural loss would be if we correctly predict and
otherwise. We can immediately see that this is a very stark loss with little nuance. There is no partial right; we are either right or wrong.
We compare that label to the true label, and we find that it is correct, and there is no update to perform. On the other hand, if we compare our prediction and the true label and find them to be different, our current loss function doesn’t tell us if we are close or not. Perhaps a significant update to our weights is needed, or perhaps only a minor update is required. What should we do?
In the last section, we saw that our loss function was lacking because there is more potential information to be gained from our prediction than is captured by the current loss function. Instead, we need a new or alternative loss function to replace our inferior one. We need a surrogate loss function.
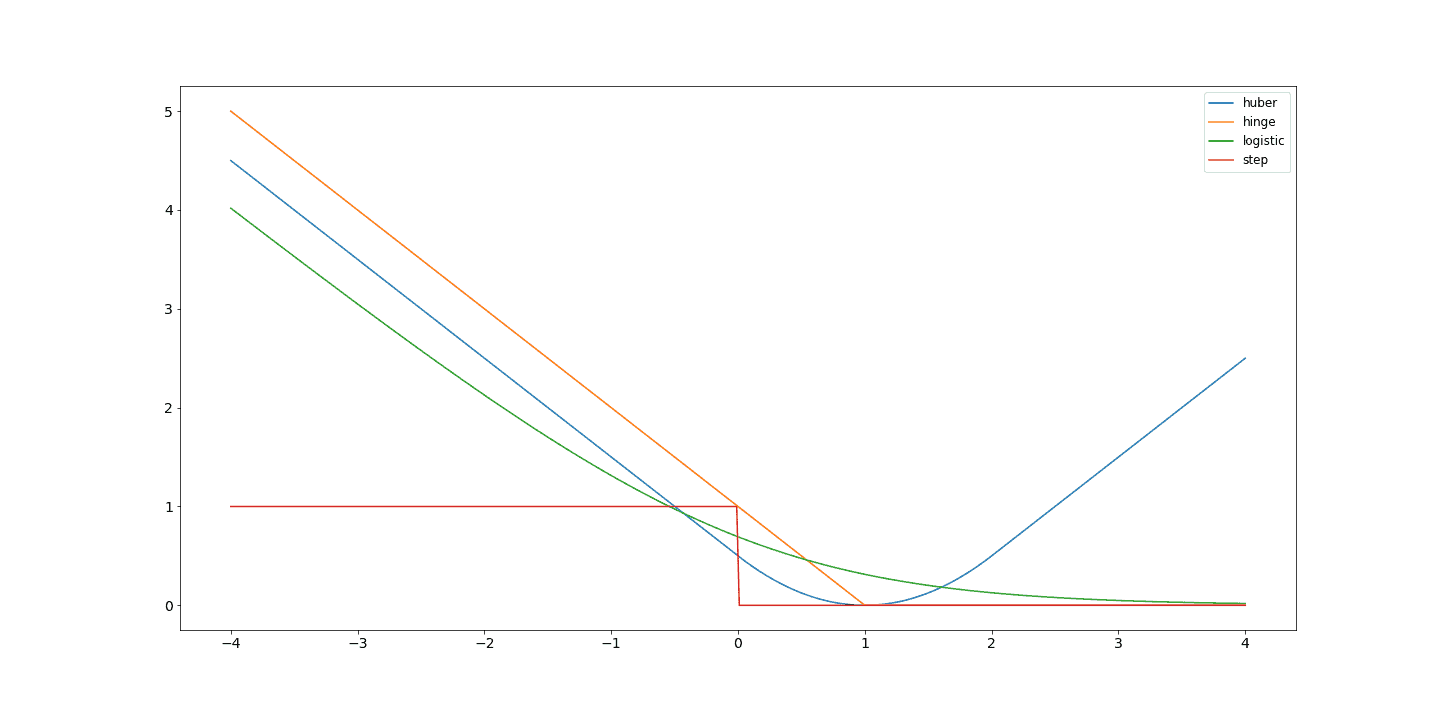
The loss function in the case of Support Vector Machines, SVM, is the Hinge Loss. This is given as . This produces a similarly harsh transition to the step function once the correct prediction is made, with an added safety margin. The logistic loss, here taken as
and Huber loss are also common loss functions. The logistic loss produces a softer transition than the hinge loss but has a very similar shape.
We look at the figure to see why the suggested surrogate loss functions are better choices. We can see the two flat planes and sharp transition of the step function. Aside from being discontinuous, the large flat regions provide very uninformative signals. The surrogate loss functions are, by contrast, continuous and provide smooth informative learning signals. We can see that the logistic and hinge functions produce similar curves; however, their behavior around 0 and transitioning is different:
A current use case for surrogate loss functions is found in the decision-focused learning field. The goal here involves predicting parameters that are fed into a decision model. Optimizing this process end-to-end can often result in an uninformative signal from the loss.
In this case, surrogate loss functions are often handcrafted to provide a more informative signal. However, this handcrafting can have drawbacks as many surrogate loss functions are non-convex, so optimization can become stuck in local minima. Recent work in this field has thus explored the possibility of learning these surrogate loss functions.
Surrogate loss functions are important to understand as they highlight the importance of understanding our problems, data, and what exactly it is we are attempting to learn.
In this article, we have shown why we need surrogate loss functions as well as examples of their effectiveness. We also highlighted the use-fullness of the concept in a modern setting and highlighted current work on the topic.