Yes, we're now running our Black Friday Sale. All Access and Pro are 33% off until 2nd December, 2025:
State Machines: Components, Representations, Applications
Last updated: February 13, 2025
1. Introduction
In this tutorial, we’ll study the basics of state machines and their applications.
At the end of this tutorial, we’ll be familiar with the concepts associated with finite-state machines, and we’ll be able to draw representations of them.
2. State Machines
Finite-state machines are one of the fundamental conceptual units of analysis in automata theory. They were initially developed to formalize the working of a system whose behavior depends upon a finite set of discrete parameters.
We commonly use finite-state machines when the behavior of a system is well-defined according to a sufficiently small set of parameters. In concrete applications, we also require an explicit definition of the rules according to which the system works, which may not always be present.
The particular configuration that the parameters of a state machine assume at a given moment is called “state” :
Because we assume that the possible values of those parameters are finite, then the number of possible states
for that machine is, consequently, also finite. If each parameter
could assume one of two binary values, for example, we’d have a total number of
distinct possible states.
For example, if :
3. Transition Rules
We can indicate the state of a state machine as , where the
indicates the discrete-time in which its state
was observed.
If we observe the configuration of a state machine over time, we could notice that the way in which its configuration changes probably presents some regularities. We could, in the limit case, observe a state machine whose state doesn’t change at all:

Non-trivial state machines, however, tend to change their state in a manner that is more interesting for us:
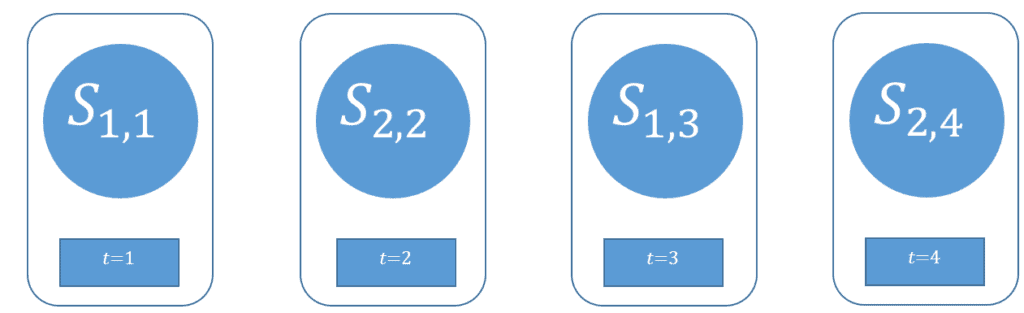
This one, for example, alternates between two states at every other interval.
If we have a complete understanding of those regularities, we can model them as a set of rules that associate a given configuration to a new one, which then updates the state of the machine.
For this reason, a state-machine does not only comprise its parameters but also the set of rules that determine how its state changes.
4. Representations
Finite-state machines can be further subdivided into groups. The most important distinction is whether we consider them as isolated systems or not.
If we consider them as isolated systems, then the rules that determine the new state can only take into account the current state. A simple update rule could be:
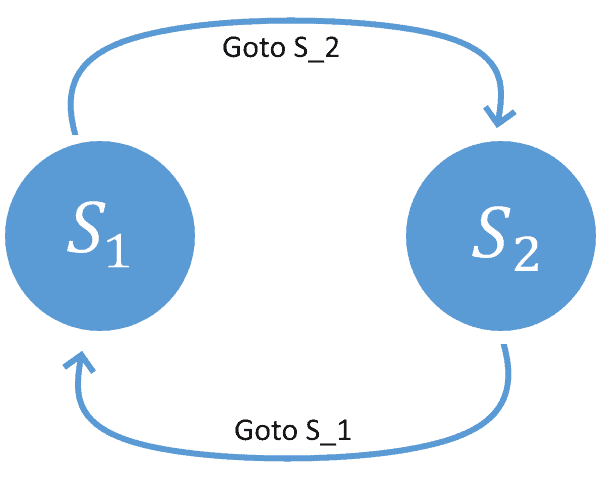
This type of automaton takes the name of Moore machine, and it doesn’t require sensing the environment. If the machine isn’t an isolated system, though, it can have an input that originates from the external environment.
In this case, the future state of the automaton is determined concurrently by the current state and by the input received. This type of automaton takes the name of Meely machine, and its typical example of that is a thermostat. For a thermostat, the temperature read by an external sensor causes the change in the state of the machine:
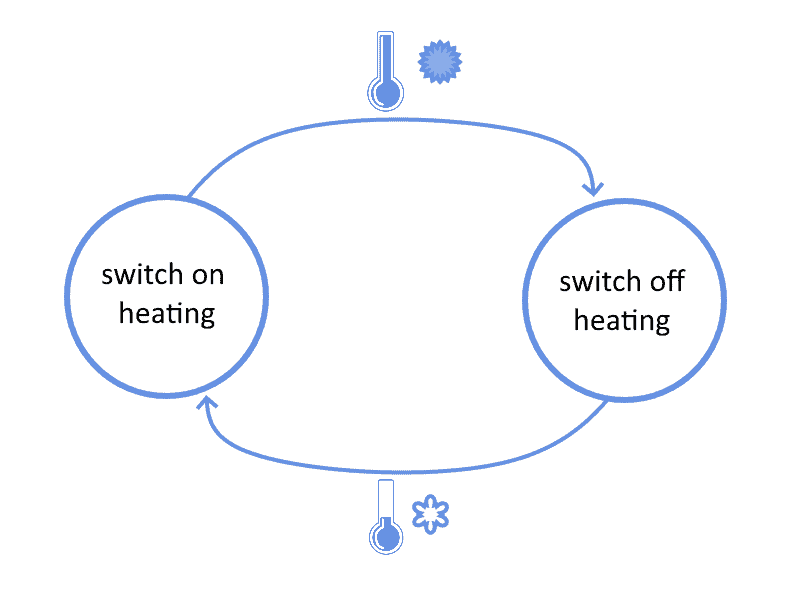
5. Applications
We’re already very familiar with finite-state machines, even though we don’t often call them by that name. Personal computers, smartphones, and hand-held calculators are all examples of machines that can assume one of a finite number of states. For this reason, we can study them as finite-state machines and apply automata theory to model their behavior.
Another common case for the application of finite-state machines is in the animation of graphical models. A video-game character that transitions from standing to walking and then to running, can for example, be modeled as a Meely machine.
We also discussed in other tutorials the usage of regular expressions to parse strings. Whenever a regex is compiled, it becomes translated into a finite-state machine. This automaton considers an alphabet, a set of states comprising an initial state, and then evaluates its final state against a set of acceptable states.
6. Conclusions
In this article, we studied the components, representations, and applications of finite-state machines.