Deterministic vs. Stochastic Policies in Reinforcement Learning

1. Introduction

In AI and Reinforcement Learning (RL), policy refers to an agent’s strategy to interact with an environment. Policies define the behavior of an agent. A policy determines the next action an agent takes in response to the current state of the environment.

A policy is a function that maps a state to an action. Depending on the context and problem at hand, policies can be deterministic or stochastic. In this tutorial, we explain the difference between these two policy types.

2. Deterministic Policy

A deterministic policy is a policy that maps each state to a single action with certainty. In other words, the agent will always take the same action given a state. This policy is represented by a function , where is the state space, and is the action space. The deterministic policy function maps each state to a single action .

The advantage of a deterministic policy is that it is easy to interpret and implement. It is also suitable for tasks where the same action should be taken for the same state every time. For example, in a chess game, the best move for a given board configuration is always the same. A deterministic policy can be the best choice to play the game optimally in such cases.

Another example that crystallizes the idea is walking along a tightrope. There is a narrow range of actions that will keep an agent balanced and moving forward. Even though the agent has many action choices, the agent only has a single choice.

3. Stochastic Policy

A stochastic policy is a policy that maps each state to a probability distribution over actions. In other words, given a state, the agent will choose an action randomly based on the probability distribution. We represent this policy by a function , where is the state space, is the action space, and is the probability of taking action in a state .

The advantage of a stochastic policy is that it can capture the uncertainty in the environment. For example, in a poker game, the agent may not always take the same action in response to the same hand since there is a probability of winning or losing depending on the opponent’s hand and how the betting has proceeded. In such cases, a stochastic policy learns the best strategy based on the probability of winning.

There are also games where a deterministic policy is exploitable, particularly if play is repeated. Take, for example, the game Rock, Paper, Scissors. A 2-player game where each player chooses an item in secret, either Rock, Paper, or Scissors, and simultaneously reveals their choice to the opponent. Each item ties with itself, loses to one item, and wins against another. In such a game, the best strategy is a stochastic strategy, choosing each item a third of the time.

4. Comparison

The primary difference between a deterministic and stochastic policy is the way in which they choose actions. A deterministic policy chooses a single action for each state, while a stochastic policy chooses from a probability distribution over actions for each state. This means that a deterministic policy always chooses the same action for the same state, while a stochastic policy may choose different actions for the same state.

Another difference is that a deterministic policy is more straightforward to interpret and implement, while a stochastic policy is more complex. A stochastic policy requires learning a probability distribution over actions, which can be challenging. On the other hand, a deterministic policy only requires selecting the best action for each state, which is relatively easy.

Deterministic policies can be more appropriate for tasks requiring precise control, where any deviation from the optimal action can significantly impact the outcome. On the other hand, stochastic policies can be more appropriate for tasks involving uncertainty or exploration, as they allow the agent to try out different actions and learn from their outcomes. The general difference between their action selection mechanisms is summarized in the figure below:

5. A Real Example

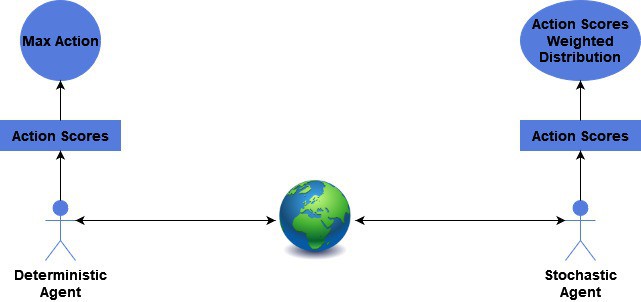
The well-understood Q-Learning algorithm uses both stochastic and deterministic policies. We are learning the Action-Value, or Q, -function in this algorithm. This function produces a value for each action in each state. This value is how good that action is for us. Our final policy, , is the action that produces the maximum value in each state. This is deterministic; if there is a tie, we use a deterministic tie-breaking rule.

That is the optimal policy. While learning, however, we use a stochastic policy. We use the Epsilon-greedy policy. This policy will choose a random action some epsilon percent of the time and otherwise will follow the greedy policy. In the case of Q-learning, doing this improves exploration of the state space during training but fully exploits the learned policy during inference. Stochastic policies are desirable during training as they can prevent the agent from getting stuck in a sub-optimal policy by exploring different actions.

6. Conclusion

In this article, we discussed a deterministic policy that maps each state to a single action and a stochastic policy that maps each state to a probability distribution over actions.

A deterministic policy is easier to interpret and implement, while a stochastic policy captures the uncertainty in the environment and prevents the agent from getting stuck in sub-optimal policies. Practitioners should choose the policy best suited for their specific task based on the uncertainty level and the environment’s complexity.