Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this tutorial, we’ll talk about Residual Networks (or simple ResNets). First, we’ll briefly introduce CNNs and discuss the motivation behind ResNets. Then, we’ll describe how the building block of a ResNet is defined. Finally, we’ll present a ResNet architecture and compare it with a plain one.
In 2012, the way we deal with computer vision problems changed forever when the AlexNet architecture was proposed by Krizhevsky. As we can see below, AlexNet consists of 5 Convolutional layers and 3 Fully-Connected layers:
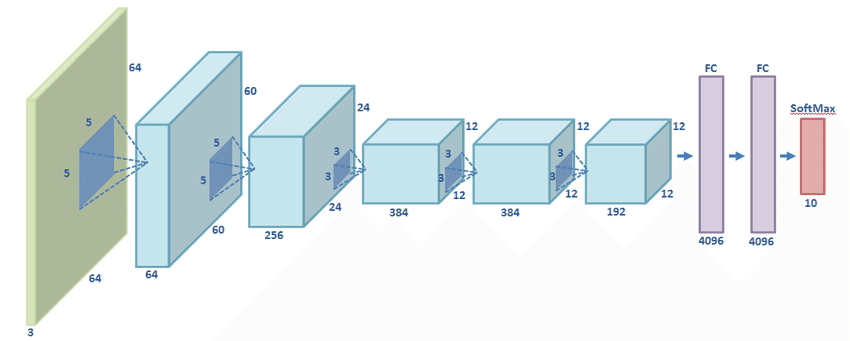
It was the first time a deep learning architecture managed to surpass all the previous traditional hand-crafted learning techniques in image classification. So, AlexNet laid the foundation for the success of CNN in visual tasks.
The core building block of any CNN is a convolutional layer followed by an activation function and a max pooling operation.
Then, researchers realized that by stacking more and more convolutional layers in a CNN, the recognition accuracy increases. The intuition behind this phenomenon is that a bigger network manages to learn more complex functions since each layer corresponds to a function.
Later, many studies came up indicating that the first layers of a CNN learn to recognize edges, the middle layers shapes, and the last layers learn to recognize more complex stuff like objects.
However, there is a limit on the number of layers you can stack while expecting to improve the performance of the network. After some time, the network overfits the training set and is not able to generalize.
That’s when the idea of ResNets came up. They manage to solve this problem since they are very deep networks that are trained without easily overfitting. Let’s see how they achieve that.
The core building block of a ResNet architecture is the residual block that can be seen in the image below:
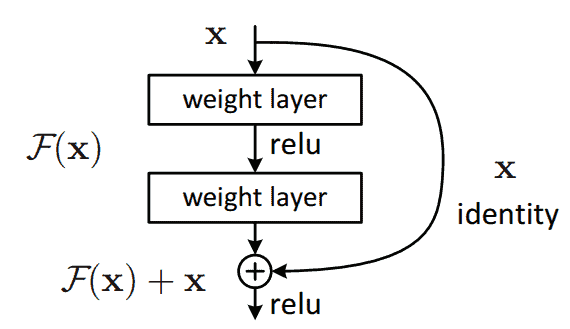
The difference between this block and a regular block from a CNN is the skip connection. We observe that the input is forwarded and added to the output value
without adding any extra parameter to the network.
The most important problem these shortcuts solve is the vanishing gradient problem that appears in large CNNs. In this problem, the gradients of the network become too small after several applications of the chain rule. So, the weights of the network are not updated, and the learning freezes. However, due to the above residual block, the gradients can now flow through the skip connections avoiding the vanishing gradient problem.
By adding the residual block at some points through the network, the authors of the ResNet architecture managed to train CNNs that consisted of a large number of Convolutional layers. In the images below, we can see a comparison between four convolutional networks. The first one is a CNN with 18 layers, and the second one is a residual version of the first network. Also, the third one is a larger network that has 34 layers, and the last one is its residual version:
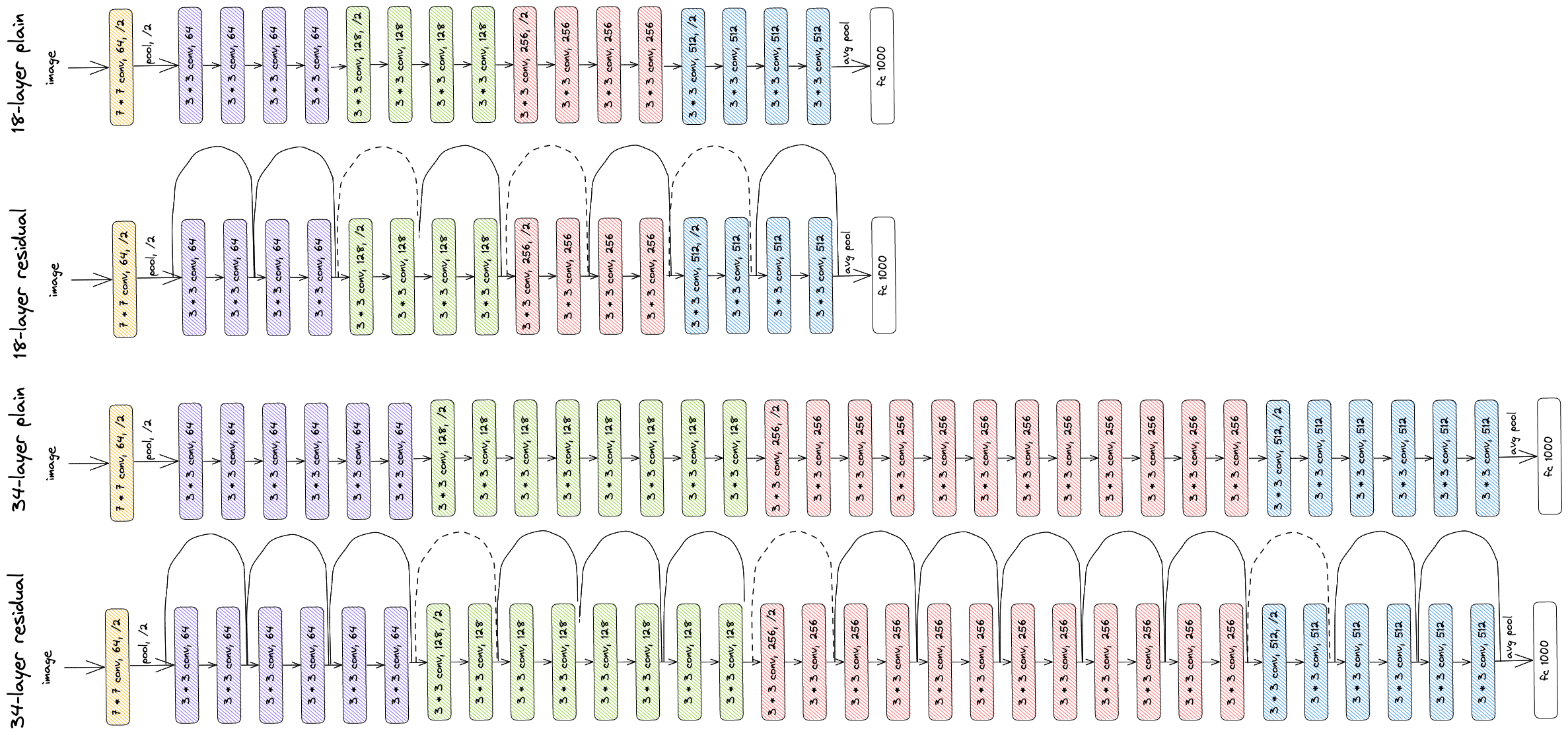
We observe that to turn a network to its counterpart residual version, we just have to insert the skip connections. The authors that proposed the ResNet architecture trained the models on ImageNet, which is a large dataset for image recognition. In the diagrams below, we can see the results where the thin curves correspond to the training error and the bold curves to the validation error:
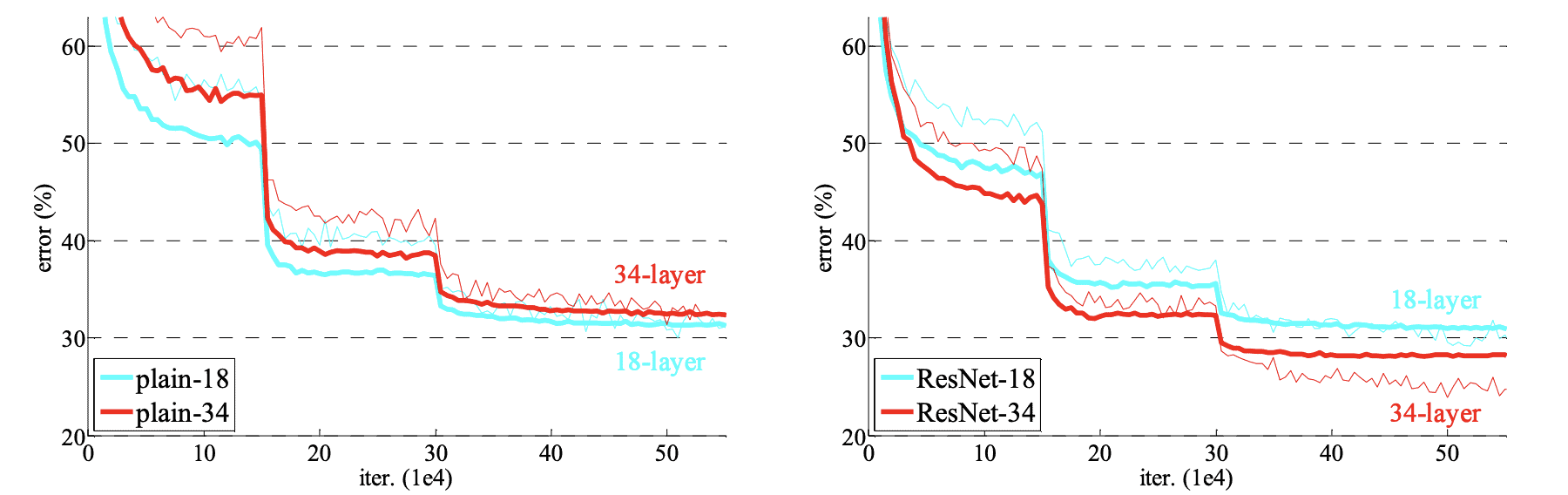
We observe that the ResNet architectures manage to converge faster than the plain ones. Also, the ResNet with the larger number of layers performed better than both the plain one and the smaller ResNet.
All these findings verify the fact that ResNet architectures deal with the vanishing gradient problem and enable us to train large Convolutional networks that learn more complex functions.
In this article, we presented the Residual Networks. First, we introduced CNNs and talked about the motivation behind ResNets. Then, we presented the building block of ResNets and some ResNet architectures.