1. Introduction
A lot of computer science problems involve splitting up some arbitrary space in regions. Such tasks often pop up in computer graphics, image processing, game development, and geospatial analysis.
Location-based services, like Google Maps, for example, have to process millions of queries based on spatial coordinates. One example would be to fetch all the supermarkets inside a given area. But doing that for millions of people at the same time is a challenging task.
That is why quadtrees and octrees became fundamental data structures in modern software development. They provide an optimal way of decomposing and querying almost any spatial information. In this tutorial, we’ll explore how these structures work and what makes them so useful.
2. One-Dimensional Case
Before diving into the theory, let’s warm up and think about a simple problem. Let’s try to divide a one-dimensional number line from the interval 1 to 6. The goal here would be to end up with a structure that will allow for an efficient lookup of intervals.
Since the number line is already sorted, the most efficient way of splitting up the space would be a cut through the middle. If we do this recursively, we can store the data inside a binary tree with the split regions as nodes:
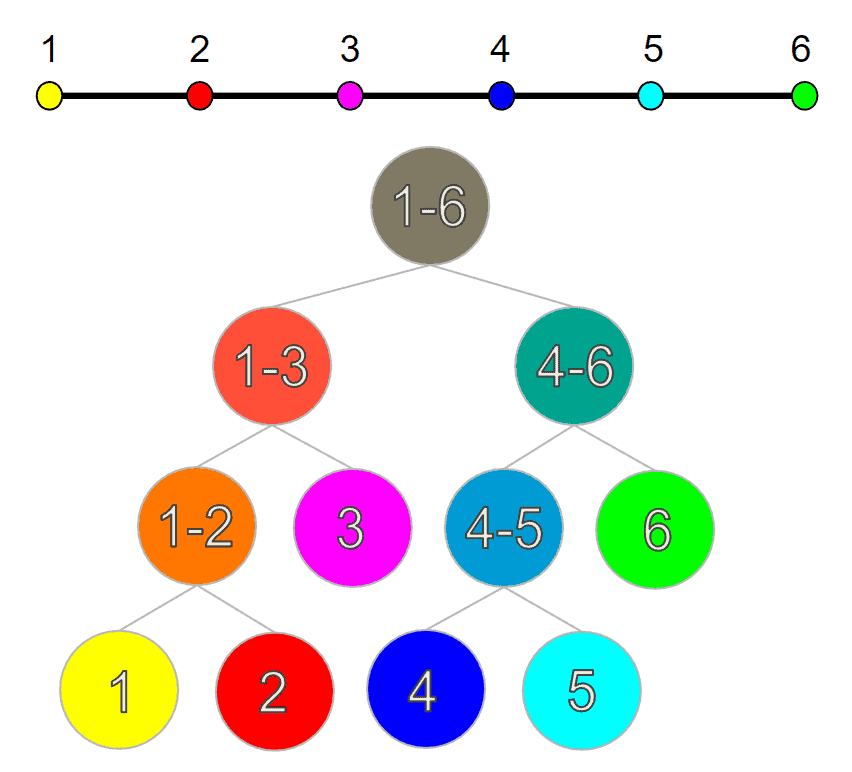
And this structure indeed allows us to conduct fast lookups over the number line intervals. This is great, but one might wonder how we can generalize this concept over to 2 or more dimensions.
3. Two-Dimensional Case
As an example, let’s imagine we have some points scattered around a 2D plane. The goal stays the same – efficient lookup of points, but this time in a certain two-dimensional region. In order to achieve similar performance, we can again use recursive splitting. We would just need to apply it over two axes instead of one. To do that, each split must always result in equal quadrants or sub-quadrants. The resulting partitioned space can be easily visualized:
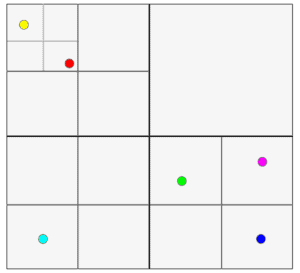
To store the sub-quadrants, we again use a tree, but this time each node would have exactly four children, each for every sub-quadrant, or no children if it’s a leaf node. This is why it’s called a quadtree.
3.1. Constructing the Quadtree
To construct such a quadtree we would first need to define some data structures like 2D points containing x and y coordinates and a bounding box that serves as a boundary:
We can then define the quadtree class itself and determine the maximum capacity of points that each sub quadrant can have. Then we can start with a unit square as the root of the tree and recursively insert points inside the tree. If the capacity has not been reached and the region doesn’t have subdivisions, we insert the point. Otherwise, we subdivide and recursively add the point to whichever node accepts it:
4. Three-Dimensional Case
Even if we go up a dimension and have points that are located in 3D space, like in a real-world physics simulation, for example, we can apply the same trick. Not a lot has changed. We can subdivide the space recursively and end up with a tree structure called an octree. The only difference this time would be that the tree must have exactly nodes describing each octant region:
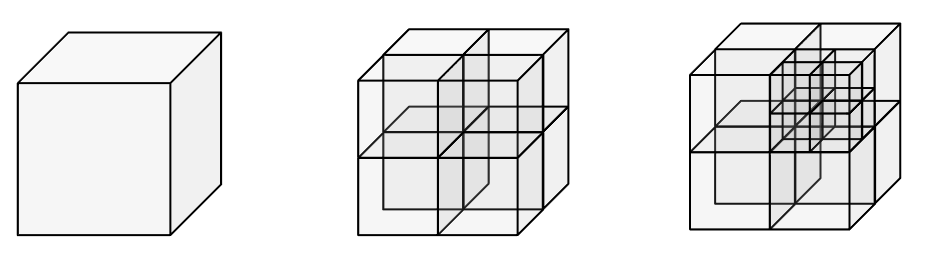
5. Conclusion
In this article, we looked into the principle behind recursively splitting trees, namely quadtrees and octrees. By illustrative examples, we explained what makes these data structures an efficient choice in many computer science areas.