1. Introduction
In this tutorial, we’ll show how to convert an expression written down in postfix notation into an expression tree.
2. Expressions
All the operators come after their arguments in the postfix representation of an expression. For example, the expression:
has the following postfix representation:
An expression tree is a graphical representation of an expression where:
- leaf nodes denote constant values or variables
- internal nodes contain operators
For example, here’s the above expression’s tree:
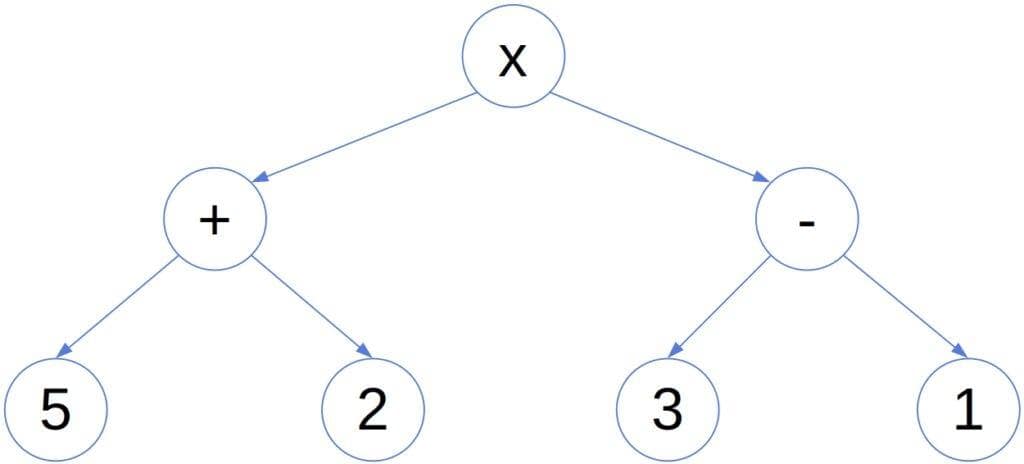
Since the order of computation is clear in postfix notation, it doesn’t need parentheses. That makes postfix expressions easier to write. However, they aren’t human-readable. To represent an expression in a readable way, we often write them down as expression trees.
So, let’s say that is the postfix representation where each
is a constant, variable or an operator. Our goal is to transform it into a tree.
3. Algorithm for Expressions With Binary Operators
First, we’ll cover the case when all the operators are binary.
That means that as soon as we hit an operator token in , we can be sure it acts on two preceding operands. So, we need to store them in a way that makes it easy to retrieve them in reverse order. A stack seems like a natural choice.
However, the trick is that operands can also be sub-expressions of the original. Therefore, we need a data structure capable of representing literals and variables in addition to expressions. For instance, we could define the following class hierarchy in an object-oriented language such as Java:
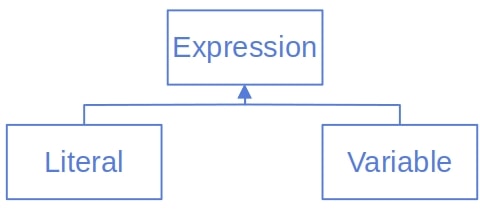
It follows the recursive definition of expressions:
- Literals and variables are expressions.
- If
and
are expressions and
is a binary operator,
is also an expression.
3.1. Pseudocode
Here’s the pseudocode:
The idea is to iterate over and handle
depending on whether it’s an operator. If not, we store it in the stack. If yes, we pop the two most recent items. The first pop returns the right operand since it’s processed the last. Then, we glue them together to make their parent node and push the new node onto the stack.
In the end, the stack holds the tree’s root.
3.2. Example
Here is how our algorithm would handle :

As we see, it didn’t need more than seven steps, which is the number of symbols in the expression.
3.3. Complexity
Since we assumed that all the operators are binary, we pop at most two items from the stack for each . Therefore, the algorithm’s worst-case time complexity is
.
3.4. Assumptions and Limitations
We assume that is an array of symbols (tokens), where each is either an operator, a variable, or a literal. If the input expression is a string, we first need to tokenize it before applying this algorithm.
Additionally, the algorithm doesn’t check if the expression is malformed. If so, building the tree will fail.
Last but not least, it assumes the operators are binary. For instance, that means it can’t handle negative numbers since the minus in -5 is a unary operator.
4. Algorithm for Expressions With Arbitrary Operators
We can adapt the algorithm to handle operators of any arity. However, we need a way to determine the number of operands for each operator symbol. To do that, we can use a hash table whose keys are the operators, and the values denote their arities.
Here’s the pseudocode:
We only changed the else branch in the loop. If is an operator, we first query the hash table to get its arity
. Then, we pop
items from the stack to get the operands. However, the stack returns them in reverse order, so we need to correct that. Afterward, the only thing left to do is to instantiate the parent node and push it onto the stack.
4.1. Complexity
Let be the operators’ maximal arity. When processing the symbol
, we pop no more than
items from the stack. Since we iterate over
symbols, the time complexity is
.
If is a constant, the complexity reduces to
, the same as for the algorithm handling binary operators only. However, we expect this one to run slower in practice because, in general, it will pop more operands from the stack.
5. Conclusion
In this article, we presented a linear-time algorithm for converting a postfix expression into an expression tree.