Playfair Cipher

1. Introduction

In this tutorial, we’ll explore the Playfair Cipher and how to use it for encryption and decryption.

2. What Is Playfair Cipher in Cryptography?

Cryptography is the practice of securing communication by converting plain text into a coded form, making it unintelligible to unauthorized individuals. One such cryptographic technique is the Playfair Cipher, invented by Charles Wheatstone in 1854.

The Playfair Cipher operates on pairs of letters rather than individual letters, making it more resistant to frequency analysis attacks. It employs a square grid, known as a key square, to determine the substitution of letters in plaintext.

2.1. Understanding the Playfair Cipher

The Playfair Cipher uses a matrix of letters (the key table), which contains no duplicates. The letters and are treated as the same letter. We form the key table by placing the unique letters of a keyword in order, followed by the remaining letters of the alphabet.

Let’s take the word as an example. First, we write down the letters of this word in the first squares of a matrix:

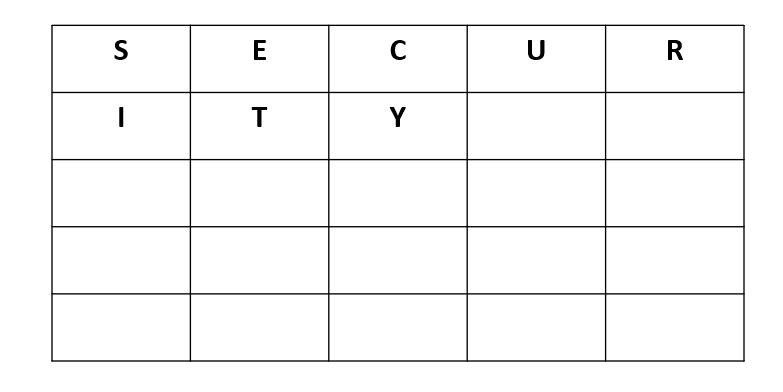
Then, we fill up the remaining squares of the matrix with the remaining letters of the alphabet, following the alphabetical order. However, since there are 26 letters and only 25 squares available, we assign both and to the same square:

When selecting a keyword, it’s vital to ensure that no letter is repeated and, notably, that the letters and don’t appear together. For instance, keywords such as , , and wouldn’t be suitable due to the violation of this rule, as they include both and simultaneously.

3. Encryption Process

The encryption process in the Playfair cipher involves a series of steps that transform a message into its encrypted counterpart.

3.1. Building the Key Square

To begin, we construct a key square using a chosen keyword. In our example, we’ll use the keyword :

3.2. Preparing the Message

Before encrypting the actual message, we must preprocess it. We treat as (effectively excluding the former from the encryption process). Also, we remove any non-alphabetic characters, such as spaces or punctuation marks.

For example, when preparing the string , we get .

3.3. Pairing the Letters

We move forward by splitting the prepared message into pairs of letters (digraph). If a digraph contains identical consecutive letters, we insert between them. Additionally, if the plaintext has an odd length, we append at the end to form a complete digraph.

For example, when dealing with the word , we divide the message into pairs of letters:

Since the digraph contains identical consecutive letters, we insert between them:

As the message has an odd length after insertion, we append at the end to make it even:

3.4. Applying Encryption Rules

There are three rules for encrypting letters in the same pair.

If both letters in the pair are in the same row of the key square, we replace each letter with the letter to its right (wrapping around if necessary).

If both letters in the pair are in the same column of the key square, we replace each letter with the letter below it (wrapping around if necessary).

If the letters are in different rows and columns, we form a rectangle with the pair and replace each letter with the letter at the rectangle’s opposite corner (moving only left or right).

Using the matrix with the keyword , let’s find the row and column of each pair and apply the encryption rules to , whose pairs are :

After applying the encryption rules to all the letter pairs, we get .

4. Decryption Process

When it comes to decrypting a message encrypted with the Playfair Cipher, the process involves reversing the operations applied during encryption.

4.1. Key Square Construction

Similar to the encryption process, the decryption process begins by constructing the key square using the keyword . The key square is a crucial reference grid that aids in decrypting the encoded message.

This key square establishes the foundation for deciphering the encrypted text during the decryption.

4.2. Decryption Rules

The decryption rules are reverse encryption rules.

When both letters in a pair are located in the same row of the key square, we replace each letter with the letter to its left, considering wrapping around if necessary.

Similarly, suppose both letters in the pair are situated in the same column of the key square. In that case, we replace each letter with the letter above it, also considering wrapping around if necessary.

When the letters are in different rows and columns, we form a rectangle using the letter pair and replace each letter with the letter at the rectangle’s opposite corner.

We delete all s between the two same letters. Then, we remove the ending if the rest of the message has an odd length.

4.3. Decryption Process

Let’s decrypt the message using these decryption rules.

The pairs are:

so we process them one by one:

• and are in different rows and columns, so they form a rectangle with corners , and . By exchanging with its opposite corner and with its opposite corner , we get
• and are in different rows and columns, so they form a rectangle with corners , and . By exchanging with its opposite corner and with its opposite corner , we get
• Continuing this process, we get .

At this point, we have . After dealing with s, we get .

5. Advantages and Disadvantages of Playfair Cipher

The Playfair cipher offers the advantage of employing polygram substitution, which involves encrypting two letters together instead of single-letter substitution. This characteristic enhances the encryption complexity, significantly raising the difficulty level for potential attackers attempting to decrypt the message without possessing the key. Thus, the Playfair cipher’s use of polygram substitution is its key strength.

The Playfair cipher has certain drawbacks. Firstly, it relies on a matrix of letters, making it unable to encrypt numbers, symbols, or non-alphabetic characters. This limitation restricts its usefulness for messages that include a wider range of characters. The relatively small key space and the patterns present in the encryption make it susceptible to statistical analysis attacks.

Additionally, it doesn’t offer perfect secrecy since the frequency distribution of the original message is preserved in the ciphertext. Analyzing the frequencies of the ciphertext makes it possible to deduce the original message, given enough ciphertext.

Therefore, the Playfair cipher is a simple algorithm, but its limitations and vulnerabilities to various cryptanalysis techniques make it less suitable for secure communication in modern contexts:

It’s considered a historical encryption technique rather than a robust solution for modern cryptographic needs.

6. Conclusion

In this article, we discussed the Playfair cipher.  It’s an early example of a cryptographic technique that has paved the way for modern encryption algorithms. Understanding its principles and processes provides insights into the evolution of cryptography.

However, for secure communication in the digital age, it’s better to use more advanced encryption algorithms such as AES (Advanced Encryption Standard) and RSA (Rivest-Shamir-Adleman). These algorithms offer stronger security and are widely adopted in various applications.