Graph Adjacency and Incidence | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll discuss graph adjacency and incidence. Also, we’ll show how to use them to represent a graph.

2. Graph

In computer science, a graph $G$ is a data structure that consists of a set of vertices $V$ and edges $E$ . An edge $e$ is a pair of vertices $(v_i, v_j)$ , where $v_i, v_j \in V$ . For example, the following picture shows a graph with $5$ vertices and $6$ edges:

3. Adjacency

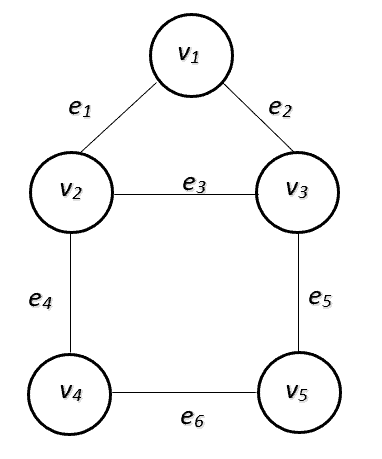
If two vertices in a graph are connected by an edge, we say the vertices are adjacent. In our graph example, vertex $v_1$ has two adjacent vertices, $v_2$ and $v_3$ . Base on this property, we can use an adjacency matrix or adjacency list to represent a graph.

3.1. Adjacency Matrix

Suppose we have a graph with $|V|$ vertices, we can use a square $|V| \times |V|$ matrix to represent the adjacency relationships among these vertices. For example, the adjacency matrix of the example graph is:

In this matrix, the number $1$ means the corresponding two vertices are adjacent. Otherwise, the entry value is $0$ . Since we have $|V|^2$ entries, the space complexity of the adjacency matrix is $O(|V|^2)$ .

To build the adjacency matrix, we can go through all edges and set 1 to the corresponding vertex-vertex entry. Therefore, the time complexity to build this matrix is $O(|E|)$ , where $|E|$ is the number of graph edges.

3.2. Adjacency List

We can also use an adjacency list to represent a graph. For example, the adjacency list of the example graph is:

In this table, each row contains a list of vertices that is adjacent to the current vertex $v_i$ . Each pair $(v_i, v_j)$ represent an edge in the graph. Therefore, the space complexity of the adjacency list is $O(|E|)$ . Similarly, we need $O(|E|)$ time to build the adjacency list.

3.3. Adjacency Matrix v.s. Adjacency List

For a dense graph, where the number of edges is in the order of $O(|V|^2)$ , the adjacency matrix and adjacency list have the same time and space complexity. However, if the graph is sparse, we need less space to represent the graph. Therefore, an adjacency list is more space-efficient than an adjacency matrix when we work on sparse graphs.

However, there are some graph operations where the adjacency matrix is more efficient to use. For example, when we want to check if there exists an edge $(v_i, v_j)$ in the graph, we can just look up the adjacency matrix in constant time to get the result. If we use the adjacency list, it will take us $O(|V|)$ time to check.

Another example is to remove an edge $(v_i, v_j)$ from the graph. In the adjacency matrix, we can just set $0$ to the corresponding entries in constant time. However, we need $O(|V|)$ time to remove the vertex from the adjacency list.

4. Incidence

In a graph $G$ , two edges are incident if they share a common vertex. For example, edge $(v_1, v_2)$ and edge $(v_1, v_3)$ are incident as they share the same vertex $v_1$ .

Also, we can define the incidence over a vertex. A vertex is an incident to an edge if the vertex is one of the two vertices the edge connects. Therefore, an incidence is a pair $\{v, e\}$ where $v$ is a vertex and $e$ is an edge incident to $v$ .

Base on this property, we can use an incidence matrix to represent a graph. For example, the incidence matrix of the example graph is:

In this matrix, rows represent vertices and columns represent edges. Therefore, the space complexity of the incidence matrix is $O(|V| |E|)$ . To build the incidence matrix, we can go through all edges and set 1 to the corresponding vertex-edge entry. Therefore, the time complexity to build this matrix is $O(|E|)$ .

The incidence matrix $C$ and adjacency matrix $L$ of a graph have a relationship of $L=C^{T}C-2I$ , where $I$ is the identity matrix.

The incidence matrix has more space complexity than the other graph representations. We normally use it in theoretic graph areas. e.g., incidence coloring of a graph.

5. Conclusion

This article provided the definitions of adjacency and incidence in graph theory. Also, we showed different ways to represent a graph using adjacency and incidence.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex