1. Overview
In this tutorial, we’ll introduce strided convolutions in neural networks. First, we’ll make an introduction to the general convolution operator, and then we’ll talk about a specific convolution technique that is strided convolution. Finally, we’ll describe the advantages and some use cases in the real world of strided convolution.
2. Convolution
Deep neural networks have proved a powerful learning technique in machine learning and AI by revolutionizing various applications from visual recognition and language generation to autonomous driving and healthcare. A central component of their success can be attributed to the substantial learning capabilities of Convolutional Neural Networks (CNNs) which are exceptionally effective in dealing with tasks involving images, graphs, and sequences.
In every CNN architecture, we can find a convolution operator that aims to exploit some type of correlation (either temporal or spatial) to learn high-level features. At a high level, we can imagine convolution as a small filter (also mentioned as the kernel) that is sliding over an input image or sequence capturing local features at each position. These local features are then combined to generate a feature map that is given as input to the next layers of the network.
3. Strided Convolution
In this article, we’ll focus on strided convolutions which improve the conventional convolutional applied in CNNs. Specifically, conventional convolution uses a step size (or stride) of 1 meaning that the sliding filter moves 1 sample (e.g. pixel in the case of images) at a time. On the contrary, strided convolution introduces a stride variable that controls the step of the folder as it moves over the input. So, for example, when the stride is equal to 2, the filter skips one pixel every time it slides over the input sample, resulting in a smaller output feature map.
In the images below, we can see how the conventional convolution (top) and a strided convolution with stride=2 (bottom) are applied in a 2-dimensional input:
4. Advantages
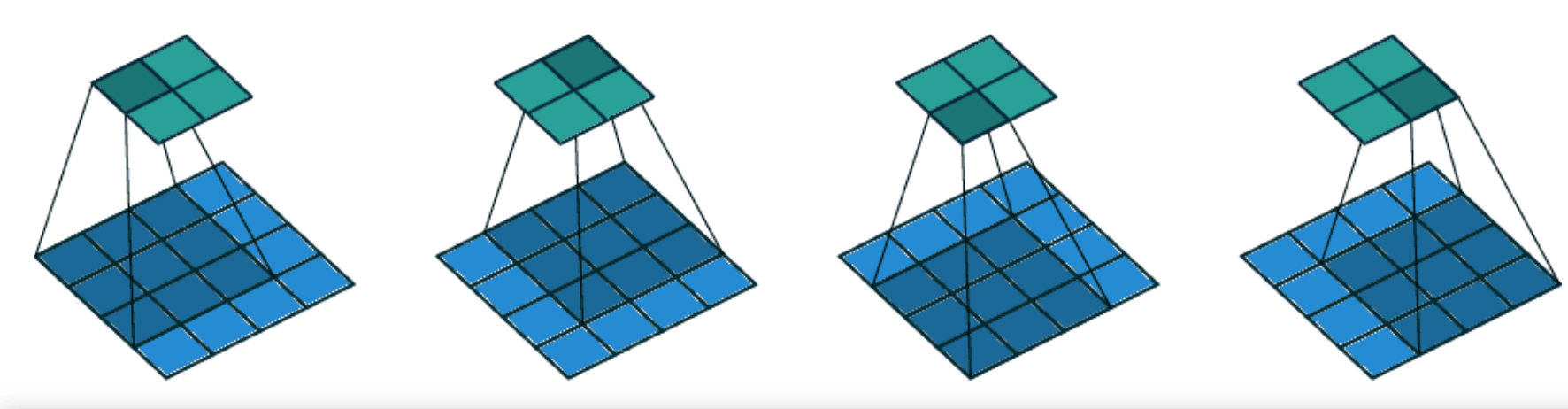
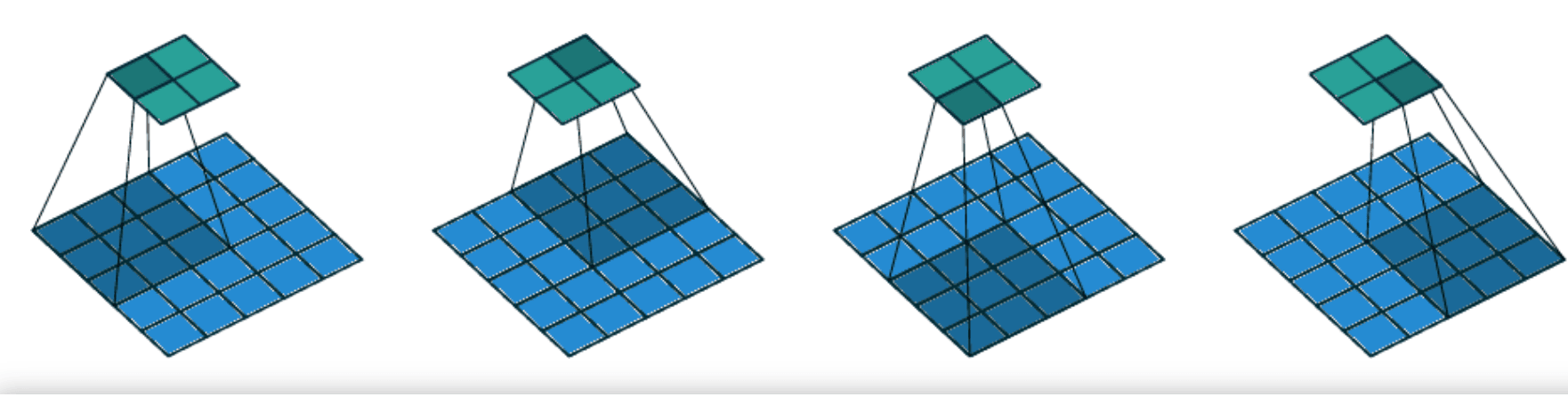
Now, we’ll move on to talk about some advantages of strided convolution over the conventional convolutional operator.
4.1. Downsampling
During strided convolution, the filter skips some pixels as it moves over the given input, performing a downsampling on the input data. This inherent downsampling comes with several advantages in the learning process. Importantly, downsampling pushes the network to focus on the most discriminative features, ignoring redundant information. In tasks like object recognition where fine-grained details may be less critical, downsampling the input image is very beneficial.
4.2. Computational Efficiency
One of the key benefits of strided convolution is reduced computational complexity. By skipping pixels, the network can process larger images more efficiently. This can be particularly important in real-time applications and resource-constrained environments.
5. Use Cases
Now that we talked about the advantages of strided convolution, let’s move on to some real-world applications where the strided convolution appears to enhance the performance of neural networks.
5.1. Image Classification
The concept of strided convolution is very beneficial in image classification, one of the most common applications of CNNs. Specifically, CNNs for image classification apply strided convolution to downsample the input image and retain only the critical information. As a result, both network training and inference are faster and lighter, a characteristic especially useful in resource-constrained settings. In addition, in cases where the input images are very large the use of strided convolution is necessary in order to fit the model in the system memory and at the same time achieve a high classification performance.
5.2. Automatic Speech Recognition
While the concept of strided convolution in CNNs started in the field of computer vision, their success expanded to many other domains like speech analysis. Specifically, in automatic speech recognition (ASR) strided convolution helps capture relevant acoustic features from audio spectrograms ignoring the low-level noisy features. By using one-dimensional CNNs with strided convolution in ASR models, researchers have achieved significant improvements in the accuracy of speech models enabling the use of better voice assistants and transcription services.
6. Conclusion
In this article, we introduced the concept of strided convolutions in neural networks. We first described the convolution operator and then we discussed the definition and the benefits of strided convolution. Finally, we mentioned some real-world applications that use strided convolution.