What Are Multi-way Search Trees?

1. Introduction

Multi-way search trees are a generalized version of binary trees that allow for efficient data searching and sorting. In contrast to binary search trees, which can only have two children per node, multi-way search trees can have multiple children per node.

In this tutorial, we’ll explore different types of multi-way search trees and common operations we can do with them.

2. Types of Multi-way Search Trees

There are several types of multi-way search trees, each with unique features and use cases. The two common types are 2-3 and B-tree.

2.1. 2-3 Tree

2-3 trees are multi-way search trees with two or three children per node.

The nodes in a 2-3 tree are sorted so that the smallest key is always in the leftmost child and the largest key is always in the rightmost child. They’re often used in applications that require moderate amounts of data, such as compilers and interpreters. Let’s look at an example of a 2-3 tree:

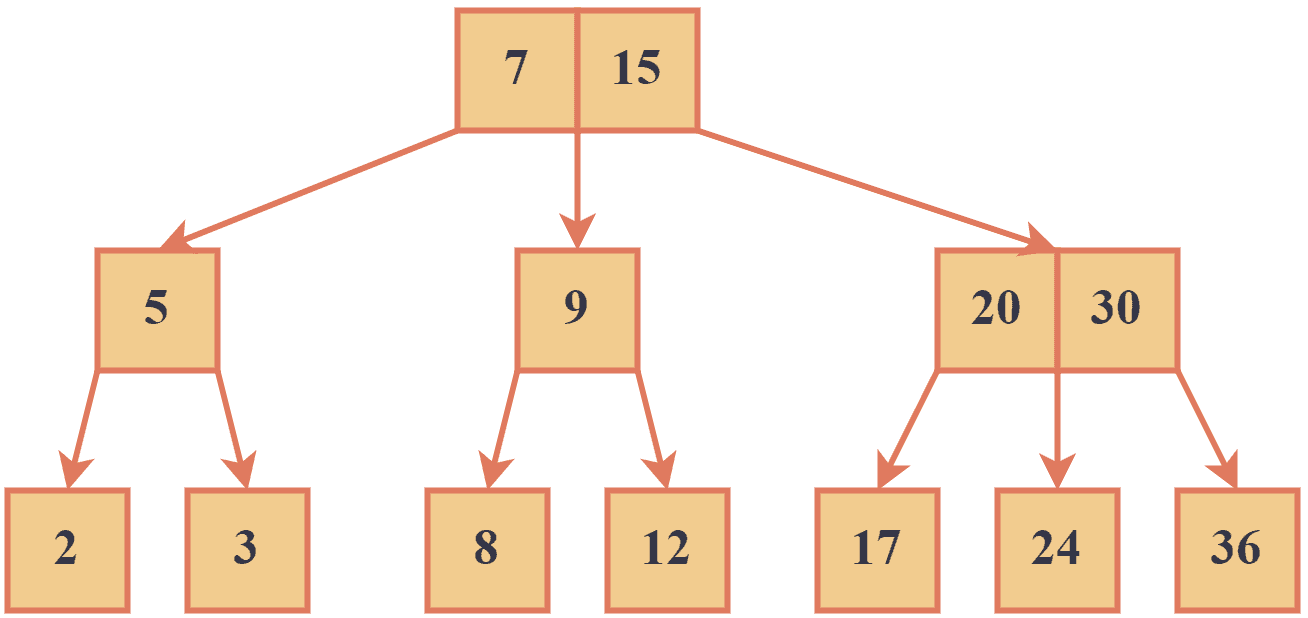
We can see that each node in the above example is either a 2-node or a 3-node.

2.2. B-Trees

B-trees have a variable number of children per node, typically ranging from 2 to hundreds.

Like 2-3 trees, B-trees are sorted so that keys are ordered from left to right. 2-3 trees are designed to optimize disk reads by ensuring that each node takes up a fixed amount of space on the disk. This allows for efficient storage and retrieval of large amounts of data and is commonly used in databases and file systems. Let’s look at an example of a B-tree:

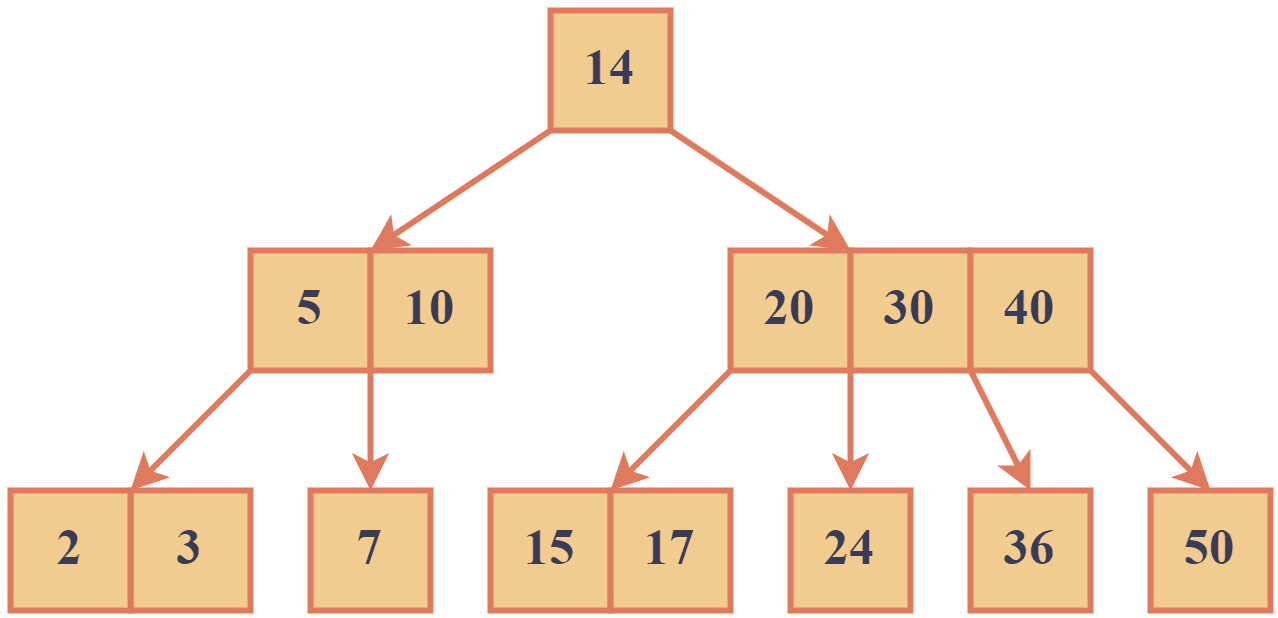
In the example above, we can see that node with keys [5,10] has two children, and the node with [20, 30, 40] has four children.

3. Insertion

To insert a new key into a multi-way search tree, we start at the root node and traverse the tree until we find the appropriate leaf node. Once we reach the leaf node, we insert the new key into its correct position. If the node is already full or becomes full after the insertion, we split it into two nodes and insert the median key into the parent node. We repeat his process recursively until the entire tree is balanced.

3.1. Example

Let’s try to insert number 8 in this tree: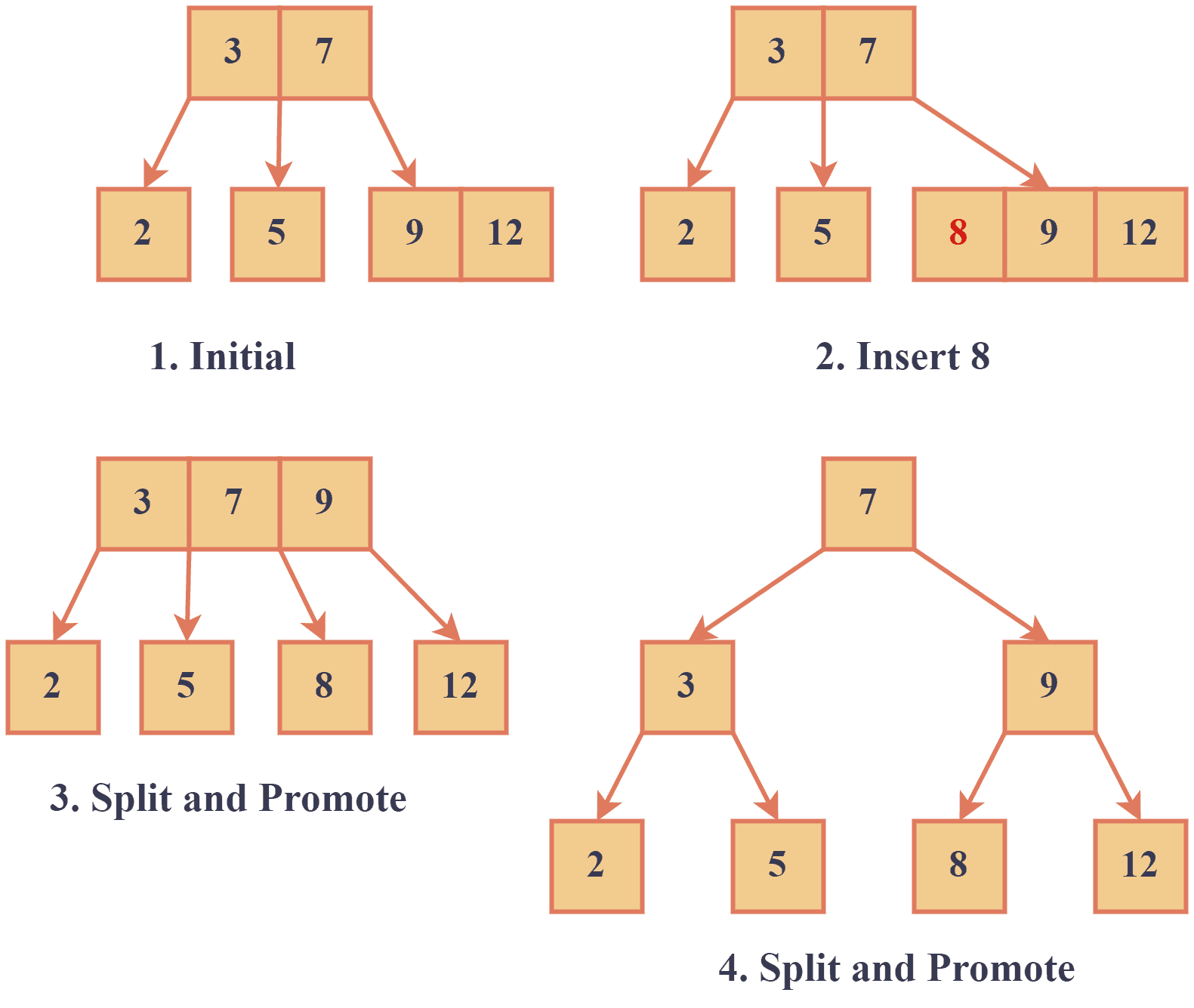

1. Starting at the root node, we compare 8 to the keys in the node and determine that it should be inserted in the rightmost child.
2. We insert 8 into it.
3. We promote the middle key (9) to the parent node ([3 7]) to create a new parent node.
4. We promote the middle key (7) to create a new parent node.

Now, the tree is balanced and satisfies the properties of a 2-3 tree.

The time complexity of insertion is time, where is the number of nodes in the tree. This is due to the balanced structure of the tree, where each node has either 2 or 3 children. This ensures that the height of the tree is at most log base 2 of .

3.2. Pseudocode

After understanding the concept and steps, let’s look at the pseudocode of the insert operation in a 2-3 Multi-way search tree.

In this pseudocode, we find the leaf node to insert the key and split the node if it has more than two keys. If the parent node is full after insertion, we split it recursively to create new nodes.

4. Searching

To search for a key in a multi-way search tree, we start at the root node and compare the key to the keys in the current node:

1. If the key matches one of the keys in the current node, we return the corresponding value.
2. If the key is smaller than the smallest key in the current node, we move to the leftmost child.
3. If the key is larger than the largest key in the current node, we move to the rightmost child.
4. If the key is between the smallest and largest, we move to the middle child.

This process is repeated until the key is found or the appropriate leaf node is reached.

4.1. Example

For example, let’s try to find 11 in this tree:

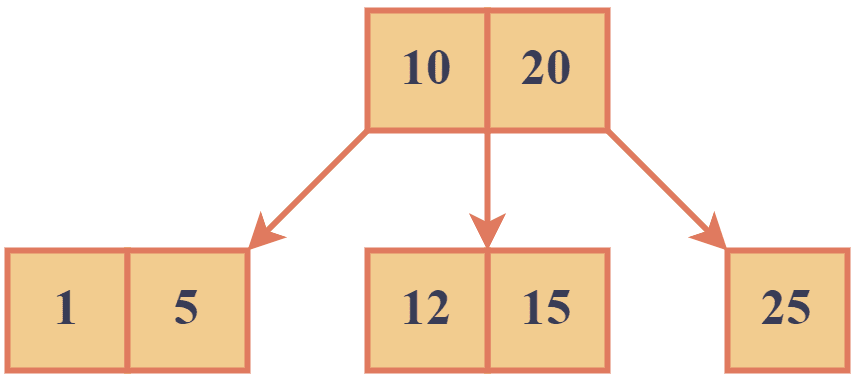
We begin at the root node to search for the key 11 in the above example. Since 11 is between 10 and 20, we move to the middle child. The middle child node contains keys [12, 15], and since 11 is less than 12, we move to the left child of the middle node. The left child node contains no keys, so we have reached a leaf node, and the key 11 is not found in the tree.

The time complexity of search in a multi-way search tree is also in the average and worst cases. This is because the tree is balanced, and each node can have at most children, reducing the search space by a factor of 3 at each level. Therefore, the search operation takes logarithmic time in the worst case.

4.2. Pseudocode

The general pseudocode for the search operation is given as follows:

In this pseudocode, we assume that the 2-3 search tree stores key-value pairs, and the search algorithm returns the value associated with the key if it is found in the tree; otherwise, it returns null.

5. Advantages of Multi-Way Search Trees

Multi-way search trees have several advantages over binary search trees, including.

Compared to binary search trees, they require fewer internal nodes to store items.

Due to their fixed height, balanced multi-way search trees can be efficiently stored on disk and accessed quickly.

Finally, multi-way search trees are generally easier to implement than other advanced data structures like AVL and red-black trees,  which have stricter balancing requirements.

5. Conclusion

In this tutorial, we explored the multi-way search tree as a flexible and efficient data structure for storing and retrieving data. Multi-way search trees offer greater flexibility by allowing multiple children per node while maintaining a relatively low memory usage compared to binary search trees.

In addition, they can be optimized for disk reads, making them an excellent choice for managing large data sets in various contexts.