Understanding the Monte Carlo Simulation

1. Introduction

Monte Carlo simulation is a computing approach that estimates and analyzes complicated systems or events using random sampling. It is called after Monaco’s Monte Carlo casino and is used in financial services, engineering, statistics, and risk analysis. It brings light to prospective outcomes and related uncertainty in a variety of circumstances.

2. Methodology and Key Concepts

Monte Carlo simulation is a technique for modeling the behavior of a system or model that employs random sampling and statistical inference. It is a computing technique rather than an exact mathematical concept. It is based on random sampling and probability theory principles. Its simulation phases and main principles are listed below:

2.1. Random Sampling

Random sampling is essential for Monte Carlo simulation, using probability distributions to generate uncertain samples and estimate outcomes.

Sampling efficiency measures how effectively the Monte Carlo simulation utilizes random samples to estimate the outputs of interest. Efficient sampling methods aim to achieve accurate results using a minimal number of samples, reducing the computational burden.

Techniques like Latin Hypercube Sampling and Quasi-Monte Carlo methods enhance sampling efficiency by distributing samples more evenly across the probability space.

2.2. Probability Distributions

To represent unpredictable uncertainty, Monte Carlo simulation employs probability distributions such as uniform, normal, exponential, and beta.

2.3. Convergence and Accuracy

Convergence is the stability of the output estimates across an increasing number of runs. To make sure that the simulation results are precise and uniform, convergence must be evaluated. Common convergence criteria are monitoring the estimates’ standard deviation or relative error and comparing them to predetermined thresholds.

2.4. Variance Reduction

By adjusting the sampling procedure and integrating further data, variance reduction techniques lessen the computing load of Monte Carlo simulations.

Techniques for reducing variation are used in the simulation estimates. These methods entail changing the sampling procedure to enhance the representation of crucial areas or lessen the variability in the simulated results. Stratified sampling, importance sampling, antithetic variations, and control variables are often employed strategies.

2.5. Confidence Intervals

Confidence intervals represent the inherent variability in the Monte Carlo simulation by offering a range of likely values for an estimated parameter or result. These ranges express the degree of certainty or likelihood that the real value lies inside the range. Factors including sample size, confidence level, and output variability all have an impact on the breadth of the confidence interval.

3. Example of Monte Carlo

Let’s take the example of flipping a coin to understand the principle behind Monte Carlo simulation.

When we flip a coin, the probability of getting “head” is . When we flip the coin times, it is hard to tell how many “heads” we’ll get. Let’s try using the monte carlo simulation in this example.

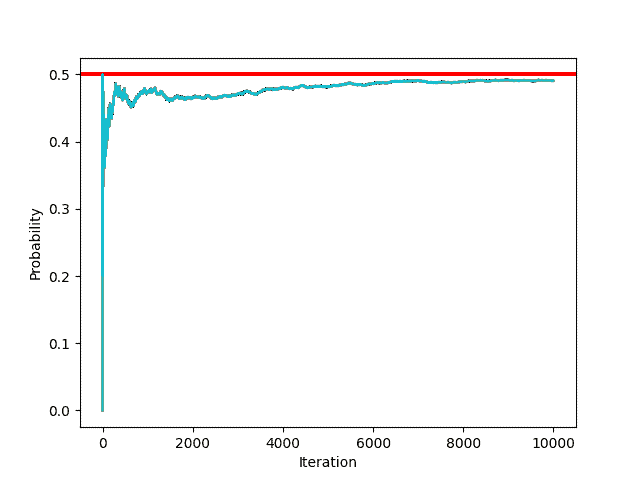
From the above example, we can see that as the number of iterations increases, the accuracy of the probability increases. This is how we can use the Monte Carlo Simulation to find probabilities experimentally.

4. Advantages and Disadvantages

First of all, the Monte Carlo simulation offers assistance with decision-making by evaluating a problem’s uncertainty. This approach enables the adoption of a broad variety of probability distributions. Additionally, it is flexible and can be applied in a wide variety of systems, and helps in handling non-linear dependencies.

On the other side, it often requires a certain amount of computational power. Furthermore, poor data quality or quantity may lead to misleading estimates. Moreover, this technique heavily relies on the input parameter, as uncertainties in it can affect the validity of the results. In addition, to represent complicated systems, Monte Carlo simulation makes assumptions and simplifies them. These assumptions might not always precisely represent real-world situations, resulting in inaccuracies or biases in the results.

5. Applications

Monte Carlo simulation has extensive applications in diverse fields, such as finance and investment, engineering and design, and risk analysis and insurance. It is used to model stock prices, simulate portfolio returns, estimate the value-at-risk (VaR), and analyze option valuations.

In engineering, it is used for design optimization, reliability analysis, and performance evaluation. In risk analysis and insurance, it is used to quantify uncertainties and assess potential losses.

Also, it has various applications in healthcare and life sciences, project management and operations, statistical analysis, and sampling techniques.

By running simulations with different scenarios and considering the probability distributions of loss variables, insurers can estimate the likelihood of different outcomes and set appropriate premiums and reserves. It also helps researchers and practitioners to study complex biological systems, optimize treatment plans, and assess the effectiveness of drug therapies. Additionally, it assists in optimizing supply chain networks and simulating production processes.

6. Conclusion

In this article, we discussed the Monte Carlo Simulation. A technique that was utilized by both von Neumann and mathematician Stanislaw Ulam in the development of the hydrogen bomb as part of the Manhattan Project during World War II.

Overall, Monte Carlo simulation is a flexible and adaptable technique that relies on random sampling, probability distributions, and statistical analysis to approximate and explore complex systems.