1. Introduction
We can formulate a reinforcement learning problem via a Markov Decision Process (MDP). Moreover, the essential elements of such a problem are the environment, state, reward, policy, and value.
A policy is a mapping from states to actions. Therefore, finding an optimal policy leads to generating the maximum reward. Hence, given an MDP environment, we can use dynamic programming algorithms to compute optimal policies, which lead to the highest possible sum of future rewards at each state.
Dynamic programming algorithms work on the assumption that we have a perfect model of the environment’s MDP. Hence, we can use a one-step look-ahead approach and compute rewards for all possible actions.
In this tutorial, we’ll discuss how to find an optimal policy for a given MDP. More specifically, we’ll learn about two dynamic programming algorithms: value iteration and policy iteration. Furthermore, we’ll discuss the advantages and disadvantages of these algorithms.
2. Policy Iteration
In policy iteration, we start by choosing an arbitrary policy 
. Then, we iteratively evaluate and improve the policy until convergence:
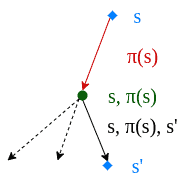
We evaluate a policy 
by calculating the state value function 
:
![\[V(s) = \sum_{s',r'}p(s', r|s,\pi(s))[r+\gamma V(s')]\]](/wp-content/ql-cache/quicklatex.com-5f242e391cba027ed209df53403106e0_l3.svg "Rendered by QuickLaTeX.com")
Then, we calculate the improved policy by using a one-step look-ahead to replace the initial policy :
![\[\pi(s) = arg\max_{a} \sum_{s',r'} p(s', r|s,a)[r+\gamma V(s')]\]](/wp-content/ql-cache/quicklatex.com-65242c0c69644f7e800aba21d1a35d9f_l3.svg "Rendered by QuickLaTeX.com")
Here, 
is the reward generated by taking action 
, 
is a discount factor for future rewards, and 
is the transition probability.
Initially, we don’t care about the initial policy 
being optimal or not. Additionally, during the execution, we concentrate on improving it on every iteration by repeating policy evaluation and policy improvement steps. Furthermore, using this algorithm, we produce a chain of policies, where each policy is an improvement over the previous one:
![\[\pi_0 \xrightarrow[]{\text{E}} v_{\pi_0} \xrightarrow[]{\text{I}} \pi_1 \xrightarrow[]{\text{E}} v_{\pi_1} \xrightarrow[]{\text{I}} \pi_2 \xrightarrow[]{\text{E}} \dotsi \xrightarrow[]{\text{I}} \pi_* \xrightarrow[]{\text{E}} v_{*}\]](/wp-content/ql-cache/quicklatex.com-23773e64ec5a8418f4a113488094fc6b_l3.svg "Rendered by QuickLaTeX.com")
Additionally, we conduct policy evaluation and policy improvement steps until the policy doesn’t improve anymore:
At the start of the policy iteration algorithm, we randomly set a policy and initialize its state value. Furthermore, the next step is to evaluate the initial policy by calculating the state value function. Moreover, the policy evaluation is an iterative process that involves continuously updating the policy’s state value until it converges.
After we complete the policy evaluation process, we move to the policy improvement phase. The main aim of this phase is to generate a new policy that is better than the current policy.
Finally, we check convergence criteria to determine if the policy has converged. To check the algorithm’s convergence, we inspect the old and newly generated policies. In case of convergence, both policies have to be the same. On the other hand, if convergence hasn’t been achieved, we go back to the policy evaluation phase and update the policy’s state value continuously until it converges.
Since a finite MDP has a finite number of policies, the defined process is finite. In the end, converging an optimal policy 
and an optimal value function 
is guaranteed.
3. Value Iteration
In value iteration, we compute the optimal state value function by iteratively updating the estimate 
:
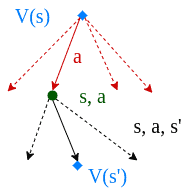
First, we start with a random value function . At each step, we update it:
![\[V(s) = \max_{a} \sum_{s',r'}p(s', r|s,a)[r+\gamma V(s')]\]](/wp-content/ql-cache/quicklatex.com-01c7fb4ec70420280d0505792c8bc824_l3.svg "Rendered by QuickLaTeX.com")
Hence, we look ahead one step and go over all possible actions at each iteration to find the maximum:
The update step is very similar to the update step in the policy iteration algorithm. Moreover, the only difference is that in the value iteration algorithm, we take the maximum number of possible actions.
Instead of evaluating and then improving, the value iteration algorithm updates the state value function in a single step. In particular, this is possible by calculating all possible rewards by looking ahead.
Finally, the value iteration algorithm is guaranteed to converge to the optimal values.
4. Policy Iteration vs. Value Iteration
Policy iteration and value iteration are both dynamic programming algorithms that find an optimal policy 
in a reinforcement learning environment. Furthermore, they both employ variations of Bellman updates and exploit one-step look-ahead:
In policy iteration, we start with a fixed policy. Conversely, in value iteration, we begin by selecting the value function. Then, in both algorithms, we iteratively improve until we reach convergence.
The policy iteration algorithm updates the policy. Hence, the value iteration algorithm iterates over the value function instead. Still, both algorithms implicitly update the policy and state value function in each iteration.
In each iteration, the policy iteration function has two phases. The first evaluates the policy, and the other improves it. Additionally, the value iteration function covers these two phases by maximizing the utility function for all possible actions.
The value iteration algorithm is straightforward. It combines two phases of the policy iteration into a single update operation. However, the value iteration function simultaneously runs through all possible actions to find the maximum action value, making the algorithm computationally heavier.
Both algorithms are guaranteed to converge to an optimal policy in the end. Yet, the policy iteration algorithm converges within fewer iterations. As a result, the policy iteration is reported to conclude faster than the value iteration algorithm.
5. Conclusion
We use MDPs to model a reinforcement learning environment. Hence, computing the optimal policy of an MDP leads to maximizing rewards over time. Moreover, we can utilize dynamic programming algorithms to find an optimal policy.
In this article, we’ve investigated two algorithms to find an optimal policy for an MDP. Policy iteration and value iteration algorithms work on the same principle. Finally, we’ve discussed their advantages and disadvantages.