1. Overview
Merge Sort is one of the most popular sorting algorithms where we divide a problem into subproblems. When the solution to each subproblem is ready, we ‘merge’ the results from the subproblems to solve the main problem.
In this tutorial, we’ll discuss the time complexity (a.k.a. Big O) of Merge Sort and also the combination that causes the worst case.
2. Two Steps of Merge Sort
The algorithm has two steps.
Step 1 is “Divide”, where the algorithm repeatedly divides the array into two halves until we reach a stage where the size of the subarray is 1:
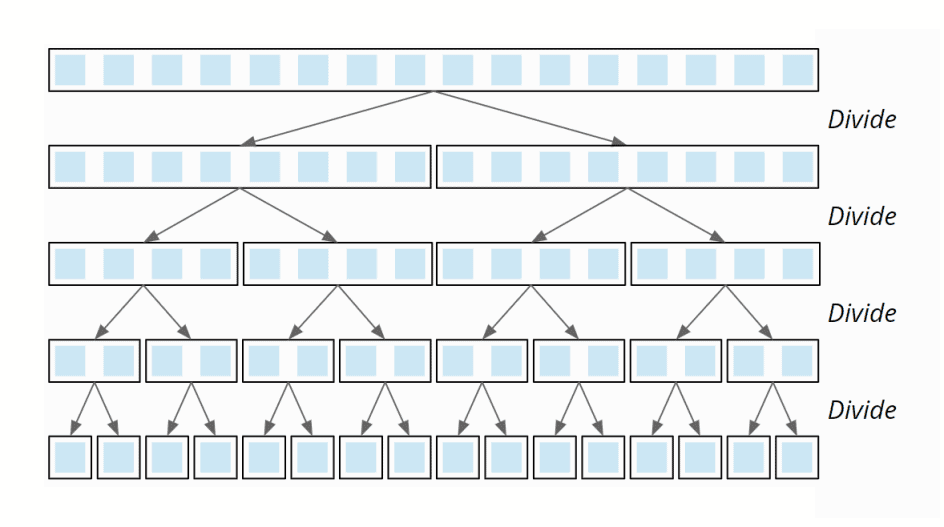
The time complexity of division function of array above (having 16 elements and = 16) is 8+4+2+1 = 15. In other words, when the size of the array is
, the time complexity of the divide function of Merge Sort is (
/2+
/4 …till 1) which is also
.
Step 2 of the algorithm includes “Merge + Sort”, where two subarrays are merged so that a sorted array is created from each pair of subarrays. In the last step, the two halves of the original array are merged so that the complete array is sorted:
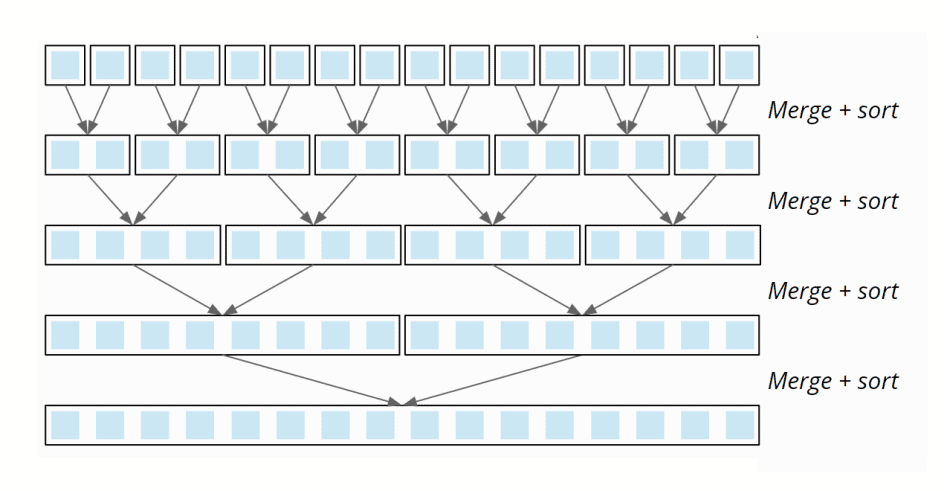
This algorithm loops through times and the time complexity of every loop is
, so the time complexity of the entire function is
.
The complexity of the entire algorithm is the sum of the complexity of two steps which is . This happens to be the worst case of Merge Sort as well.
3. The Worst Case of Time Complexity for Merge Sort
Time complexity can be improved if the number of comparisons can be reduced while doing merge and sort. However, no optimization is possible if the left and right sub-arrays involved in the merge operation have alternate elements of the sorted array. For example, if the left and right sub-array are {1,3,5,7} and {2,4,6,8} respectively, then every element for both arrays needs to be compared at least once, which will result in the worst time complexity.
The process flow of the algorithm will look below:
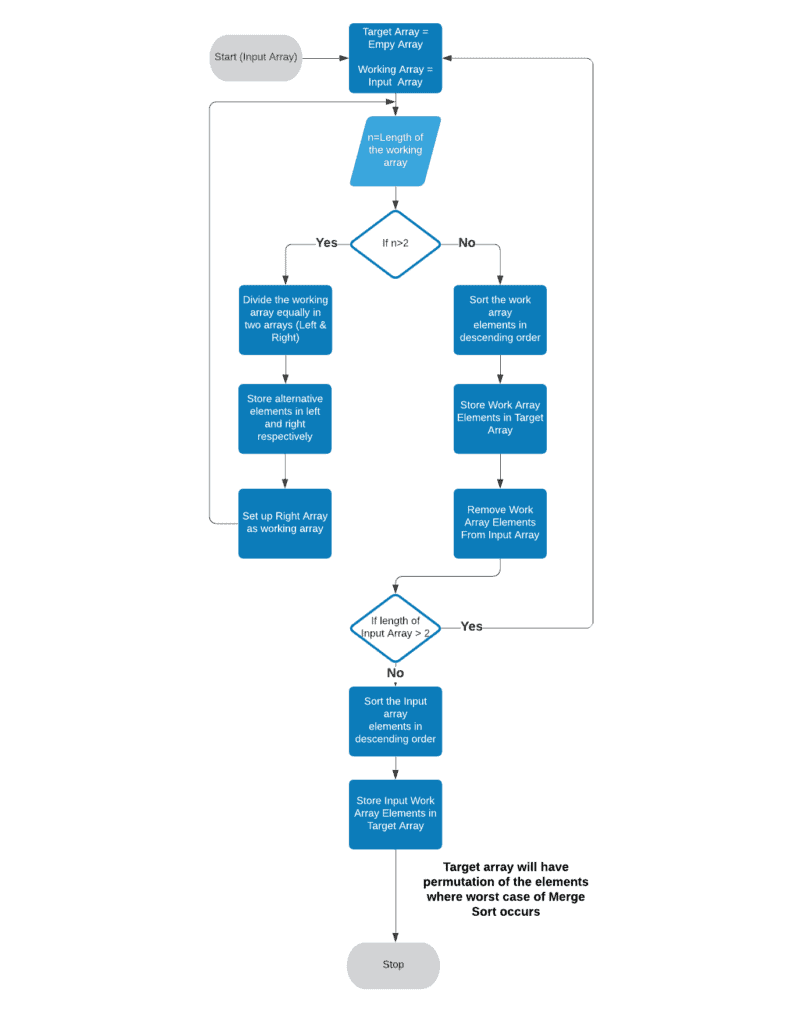
If we use this algorithm on array {1,2,3,4,5,6,7,8}, we’ll find {5,1,7,3,6,2,8,4} as the combination that’ll produce worst complexity for merge sort as shown below:
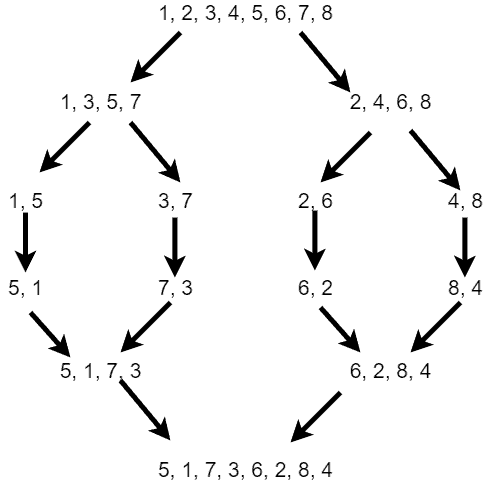
4. Conclusion
In this article, we discussed the worst time complexity of Merge Sort, which is . It occurs when the left and right sub-arrays in all merge operations have alternate elements.