Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this tutorial, we’ll study Menger’s theorem on finite graphs. We define a graph with vertex set
and edge set
as finite when both sets are finite.
Karl Menger formulated this theorem in the year 1927 while he was studying graph connectivity problems. It was the pioneering work in that era because it paved the way for advanced theorems in graph connectivity (max-flow min-cut, strongly connected components) and duality in linear programming.
Let’s consider a finite undirected planar graph . Here, we choose two non-adjacent vertices
and
from
:
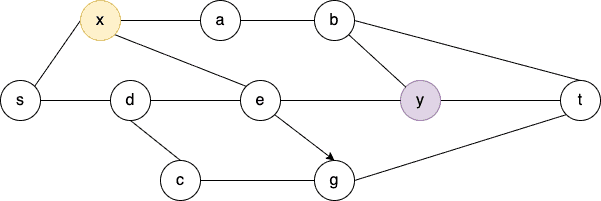
Now, we want to disconnect from
. So, how can we do it?
For this, we first need to find out how many internally disjoint paths there are between both and
:
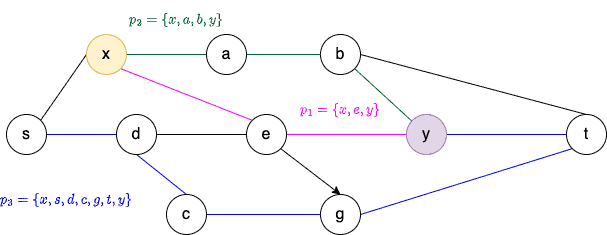
If we have 3 disjoint paths ,
, and
between them, then we can completely disconnect
and
by removing all edges on
,
, and
:
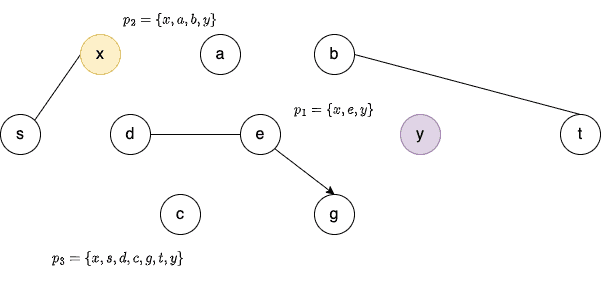
Menger’s theorem is about the number of nodes and edges we need to remove from a graph to disconnect two non-adjacent vertices.
It has two formulations: the vertex and edge versions.
Let and
be distinct non-adjacent vertices in a connected graph
.
Further, we define a vertex subset as a
vertex-separator if the vertices
and
are in different components of the sub-graph
(the sub-graph we get by removing from
all the nodes
and the associated edges).
This also means there’s no path from to
in
. Thus,
separates
from
in
. We call
a
vertex-cut.
The vertex case of Menger’s theorem states that for any undirected graph and non-adjacent vertices
and
, the minimum number of vertices in a
vertex-cut is equal to the maximum number of pairwise internally disjoint paths between
and
.
The edge case is similar.
We define as a
edge-separator if the vertices
and
lie in different components of the sub-graph
(sub-graph obtained after deleting
from
). By analogy with the vertex case, we also call it an edge cut.
The edge version of Menger’s theorem states that for any undirected graph and non-adjacent vertices
and
, the number of edges in the minimum edge-cut for
and
is equal to the maximum number of pairwise edge-disjoint paths from
to
.
We now move on to an example to understand these definitions. Here, we have a graph :
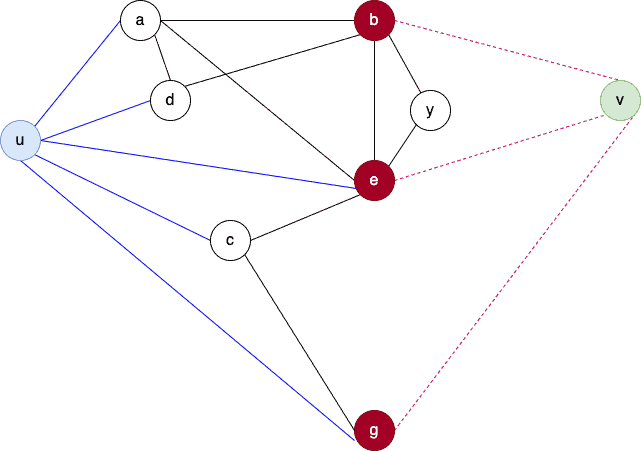
The set (red nodes) is the minimum
vertex-cut, and the edge set
(dashed pink) is the minimum
edge-cut.
They correspond to a three-element set of internal disjoint paths (paths that don’t share any vertex other than and
)
.
No larger set of paths is disjoint internally and connects and
. So, the theorem works: the minimal edge and vertex cuts have the same cardinality as the maximum disjoint path set.
We’ll use induction on the number of edges to prove the theorem.
To improve exposition, we define as the set of all neighbors of
and
as the set of all neighboring vertices to
.
For with no edges, the minimum
separator is the set of common vertices of
and
.
The vertices in correspond to paths between
and
, which proves the base case.
Let’s say our graph has
edges and assume that Menger’s Theorem holds for all graphs with
edges.
We aim to prove that the maximum number of independent paths between and
equals
, the size of the minimum
cut in
.
To do so, let be an edge in
, and let
be the minimum
vertex cut in
:
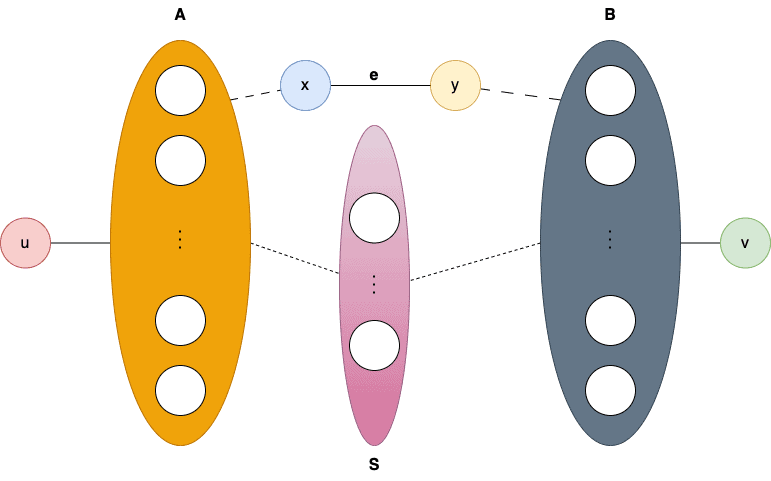
If has
vertices, it’s the minimum
cut for
. Since
has
edges and Menger’s theorem holds for it by the inductive hypothesis, it also holds for
.
Otherwise, has
vertices. Why? That’s because if it had fewer nodes, the minimum
cut in
would also have fewer than
vertices, which is a contradiction.
Now, each path in
is:
The minimum separator of and
is also the minimum separator of
and
and has
vertices. So, there are
paths from
to
. The same goes for
and
. Concatenating those paths, we get at most
paths from
to
, which we wanted to prove:
without
and one through
.
The max-flow min-cut theorem is the generalized version of Menger’s theorem.
In graph and optimization theory, the max-flow min-cut theorem states that in a flow network created from a directed acyclic graph, the maximum amount of flow that can pass from the source node to the sink node
is equal to the total weight of the edges in the minimum
cut.
Let’s understand this with an example. So, we have a directed acyclic graph whose each has a flow and a capacity:
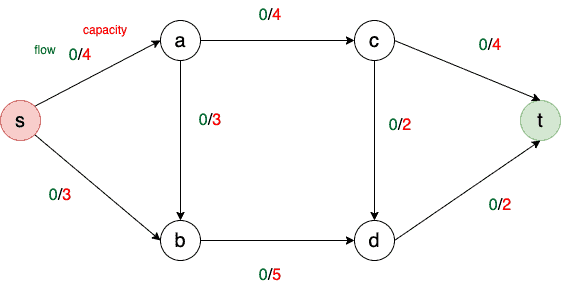
The flow is the quantity of load (processing power, network requests, etc.) we are currently transporting over that edge, and the capacity is the maximum load.
Initially, we set the flow over all edges to 0. Now, we have two minimum edge separators:
, and
. But,
has a total capacity of 7 (4+3), and
has a total capacity of 6 (4+2). So, our minimum cut is 6, and we can send a maximum of 6 units of flow from
to
in
:
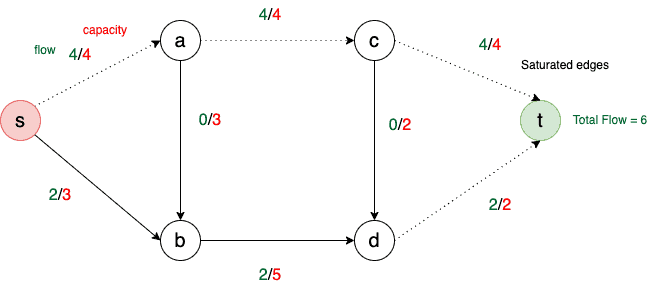
In this article, we explained Menger’s theorem. It tells us that for an undirected graph with two non-adjacent vertices and
, the minimum number of vertices needed to disconnect both of them is equal to the maximum number of the internally disjoint paths between
and
.