Yes, we're now running our Black Friday Sale. All Access and Pro are 33% off until 2nd December, 2025:
How Do Markov Chain Chatbots Work?
Last updated: February 28, 2025
1. Overview
The Markov chain is a fundamental concept that can describe even the most complex real-time processes. In some form or another, this simple principle known as the Markov chain is used by chatbots, text identifiers, text generation, and many other Artificial Intelligence programs.
In this tutorial, we’ll demonstrate how simple it is to grasp this concept. Primarily, we’ll use the Markov theory to gain a certain way of learning, which helps create a chatbot capable of carrying on a meaningful conversation.
2. What Is a Markov Chain?
This is a concept that is used in many places, from statistics to biology, from economics to physics, and of course in machine learning, such as text generation and chatbots.
2.1. Basic Concept of Markov Chain
To understand this concept, let’s start with a simple example:
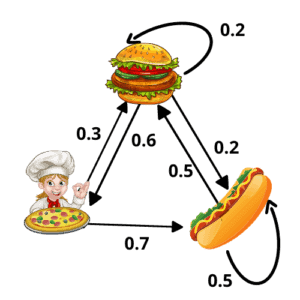
Let’s assume there’s a restaurant that serves only three types of foods hamburger, pizza, and hot dog, but they follow a weird rule: on any given day, they serve only one of these three items, and it depends on what they had served yesterday. In other words, there’s a way to predict what they will serve tomorrow if we know what they are serving today.
So, for example, there’s a chance that tomorrow will be a pizza day, given that today is hamburger day, which is represented as weighted arrows in the image above.
The arrow originates from the current state and points to the future state. The diagram above is simply a Markov chain.
2.2. Properties of Markov Chains
Let’s discuss some properties of the Markov chain. Firstly, the most important property is that the future state depends only on the current state not the steps before. Mathematically we can say depends only on the
step not the complete sequence of steps that came before {n}:
Let’s understand it a little better, suppose the restaurant served pizza on the first day, hamburgers on the second, and pizza on the third day. Now, let’s see the probability that they will serve hot dogs on the fourth day? Well, we just need to look at the third day, and it turns out to be . This is the heart of the Markov chain, and it’s known as the Markov property.
Then, the second important property is that the sum of the weights of the outgoing arrows from any state is equal to . This has to be true because they represent probabilities, and for probabilities to make sense, they must add up to one.
At first glance, this might not seem very impressive, but on a closer look, we can see that these properties make our life a lot easier while we tackle some complicated real-world problems. So, let’s now explore how to use this concept in a real-world problem, such as chatbots.
3. Markov Chain in Chatbot
We’ll now explore how we can use some of the information above regarding artificial intelligence (AI) development, especially when we have a user sentence in a response situation. Then, perhaps, we can sort of use this Markov theory to gain a certain type of way of learning and a certain type of response as we can get from a chatbot.
To achieve that, we’ll start by explaining how to chain words together and how we can use statistics for various reasons within using these words and word chains.
3.1. Chain Words
There are examples of Markov chain, especially in general use. For example, when we send a message and when typing a word, some program not only guesses what type of word actually trying to type to aid in spelling but also predict what word will probably come next:

So, as we use the phone and send numerous texts, we used to say one word like “Hello” to greet a man named “Bob” all the time. In other words, every time we send a text message, we repeat, “Hello Bob.” So, the phone program learns that whenever we say “Hello,” the word “Bob” will most likely follow. Because we taught the phone to do so, statistically, the word “Bob” will always come after “Hello”.
There’re different ways to create statistics because there’re precise ways and imprecise ways. Let’s now dig deeper into the principle of the Markov chain. Here’s some example to give us an idea about what the ratio is in regards to chaining words:
| Ratio | Key Word | Follow Word | Precision |
|---|---|---|---|
| 1:1 | Hello | Bob | Less precise |
| 2:1 | Hello Bob | Smith | More precise |
| 1:2 | Hello | Bob Smith | Imprecise |
So, the ratio means one word following one keyword, the
ratio means one word following two keywords, and the
ratio means two words following one keyword.
Now, let’s use the Markov chain with the ratio . We’ll use the following sentence “I want two pizzas, and I want a hamburger.”. So, we start with “I want” as key and “two” as follows (ratio 2:1), then “want two” as key and “pizzas” as follows. The following words may be any collection holding many “items” as we can have more than one follow word for a given pair of words. In this example, we’ll have “I want” two times, followed first by “two” then by “a”. So, in the end, we’ll have a table looking like this:
| Key Word | Follow Word |
|---|---|
| I want | Two, a |
| want two | pizzas |
| two pizzas | and |
| pizzas and | I |
| and I | want |
| want a | hamburger. |
3.2. How Do Markov Chain Chatbots Work?
The text generated by the Markov chain chatbot does not necessarily make any sense, but it can be entertaining to read. It has the same principle as chaining words while using a chat text as input (for training). Let’s break it down into steps using this simple chat text as an example:
Bot: Welcome to the THREE DAYS restaurant!
User: Hello.
Bot: Hi! Today is a hamburger day! Would you like to make an order?
User: Yes! I want a Whopper Hamburger.
Bot: Make it a meal?
Use: Yes!
Bot: You selected a Whopper Combo Meal! Where would you like to pick up the order?
Similar to chaining words, The Markov chain chatbots use a sentence as a key and another sentence as follows. So, we start with “Hello.” as a key sentence and “Hi! Today is a hamburger day! Would you like to make an order?” as follows, then “Yes! I want a Whopper Hamburger.” and “Make it a meal?” as follows. In other words, we are trying to generate a reply to the user using the Markov chain.
The follow sentences may be any collection holding many “items” as we can have more than one follow sentence for a given key sentence. For example, when the user says “Hello.” the bot may reply with “Hi! Today is a hamburger day! Would you like to make an order?”, “Hi, there! How may I help you” or simply “Hello! Do you want to see the discount offers for today?”. Here comes the utility of calculating the probability of each follow sentence to come after a key sentence. So, simply we can choose the follow sentence that has the highest probability among the candidate follow sentences to be a reply for the user key sentence.
In the end, based on the chat text above, we’ll have a table looking like this:
| Key | Follow |
|---|---|
| Hello. | Hi! Today is a hamburger day! Would you like to make an order? |
| Yes! I want a Whopper Hamburger. | Make it a meal? |
| Yes! | You selected a Whopper Combo Meal! Where would you like to pick up the order? |
Please remember that we don’t have to use only one sentence that follows a key sentence. We can use 2 or 15 sentences as follow sentences. The difference is that if you use “longer” building blocks, the chatbot will appear more accurate. This is because the bigger the input, the more follow sentences we will have for key sentences and will then have a “smarter bot” so we can “train” the bot by adding more text.
4. Conclusion
In this tutorial, we’ve discussed the basic concept of a Markov chain and how understanding its principle can help develop a smart bot capable of carrying on a meaningful conversation. We’ve also gone over the principle of a Markov chain in a chatbot and how it works.