How to Determine if a List of Polygon Points Are in Clockwise Order

1. Overview

There are several approaches to determine whether a list of polygon points is ordered clockwise or counterclockwise.

In this tutorial, we’ll create a simple algorithm to determine the polygon points’ orientation. Furthermore, we’ll revise and use some formulas for the area computation. We assume having a basic knowledge of polygons, and we’ll also use basic definitions of linear algebra.

2. Order of Polygon Points

Let’s recall the way the polygon is stored in memory. Assume $P$ is our polygon. It consists of $n$ points. Therefore, we can represent $\boldsymbol{P}$ as $\boldsymbol{P = (P_{0}, P_{1}, ..., P_{n - 1})}$ , where $\boldsymbol{P_{i} = (x_{i}, y_{i})}$ . So the shape of $P$ is represented as the list of points.

We’ll also define another polygon $P^{'} = (P_{n - 1}, P_{n - 2}, ..., P_{0})$ . It’s important to note it consists of the same points in a reversed order. $P$ and $P^'$ are two different polygons, which look absolutely the same and have equal shapes and areas.

What differs between them is their point orientation. If the points in $P$ are oriented clockwise, then point orientation in $P^'$ is counterclockwise and vice versa:

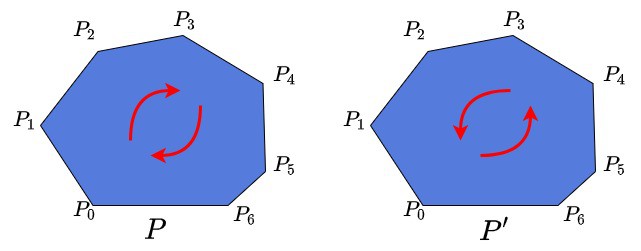
We’ll use this information about point orientation further in the tutorial. Moreover, as previously mentioned, the areas of $\boldsymbol{P}$ and $\boldsymbol{P^'}$ are numerically equal, but the signs of the areas are different.

3. Area Computation

There is a simple linear-time algorithm for the 2D polygon area computation. The algorithm introduces a formula for the area. We’ll briefly discuss the key aspects of the polygon area calculation, as well as use this formula in our point orientation algorithm.

The area of a shape can either be positive or negative. If the shape is represented as a list of points, then it depends on the orientation of the points. Let’s briefly remember the formulas for calculating the areas of triangles and polygons.

3.1. Area of a Triangle

Now let’s suppose a triangle $T_{ABC}$ is defined by 3 points $A(x_{1}, y_{1})$ , $B(x_{2}, y_{2})$ , and $C(x_{3}, y_{3})$ :

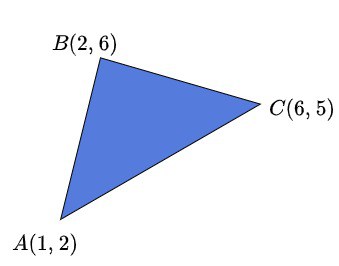
The area of this triangle can be computed with a simple formula from linear algebra: $S_{T} = 1 / 2 * \begin{vmatrix} B - A & C - A\end{vmatrix} = 1 / 2 * \begin{vmatrix} x_{2} - x_{1} & x_{3} - x_{1} \\ y_{2} - y_{1} & y_{3} - y_{1}\end{vmatrix}$ $= 1 / 2 * (( x_{2} - x_{1}) * ( y_{3} - y_{1}) - (x_{3} - x_{1}) * (y_{2} - y_{1}))$ .

If we shift our triangle to make point $A$ be $A(0, 0)$ , the area of the triangle won’t change:

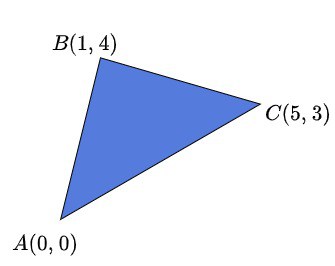
However, the formula of area computation will be a bit simplified:

$S_{T} = 1 / 2 * \begin{vmatrix} B - 0 & C - 0\end{vmatrix}$ $1 / 2 * \begin{vmatrix} x_{2} - 0 & x_{3} - 0 \\ y_{2} - 0 & y_{3} - 0\end{vmatrix}$ $= 1 / 2 * ( x_{2} * y_{3} - x_{3} * y_{2})$ .

3.2. Area of Polygon

Now we can calculate the area of a polygon using the formula for the triangle area. The idea of the approach is simple. It uses the decomposition technique. We can decompose the polygon of $n$ points to $n$ triangles. To do this, we choose the arbitrary point $Z$ , usually $Z = Z(0, 0)$ .

After that, we can compute the areas of $n$ triangles. Assume we have a polygon represented with the set of $n$ points ${P_{0}, P_{1}, ..., P_{n - 1}}$ . We form a triangle by picking points $Z$ , $P{i}$ , and $P_{i + 1}$ with $i \mod n$ , $\forall i \in {0, 1, ..., n - 1}$ . Then we sum up all the areas to get the area of the entire polygon.

The final formula that computes the area of the polygon:

$S_{polygon} = 1 / 2 \times \sum_{i=0}^{n - 1} (x_{i} * y_{i + 1} - y_{i} * x_{i + 1})$ , where $v_{i} = (x_{i}, y_{i})$ with $i \mod n$ .

It’s important to remember that the area of the polygon can be either positive or negative. It depends on the chosen point for decomposition and order of the vertices.

4. Algorithm

Let’s define a simple Signum function $Signum(x)$ . It takes an arbitrary number $x$ as a parameter and returns only three values. If $x < 0$ , $Signum(x) = -1$ . If $x > 0$ , $Signum(x) = 1$ . Finally, if $x = 0$ , $Signum(x) = 0$ . We may notice this function gives us information about the sign of the number.

Now let’s introduce an algorithm for getting the points orientation of polygon $P = (P_{0}, P_{1}, ..., P_{n - 1})$ . First, we compute the signed area by the above formula to get the number $S_{polygon}$ . Second, we compute $\omega = Signum(S_{polygon})$ . Finally, we compare $\omega$ with zero. If $\omega > 0$ , then the points are oriented counterclockwise.

Similarly, if $\omega < 0$ , then the points have a clockwise orientation. We wouldn’t expect the case when $\omega = 0$ . That would mean the area of the polygon is 0. In that case, it’s probable that the polygon was not correctly defined.

5. Time and Space Complexity

The time complexity of the above algorithm is $\boldsymbol{O(n)}$ , where $n$ is the number of points of the polygon. It takes linear time to compute the area. After that, it takes $O(1)$ time to learn whether the area is positive or not. Thus, the final complexity is $O(n) + O(1) = O(n)$ .

The space complexity is $\boldsymbol{O(1)}$ because we only need one variable to store the area.

6. Conclusion

In this article, we’ve introduced an algorithm, which helps to determine polygon point orientation in linear time. Furthermore, we’ve recalled a simple approach to compute the area of a polygon. There exist several other techniques for determining point orientation; however, all of them are based on this simple idea.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex