What Does Learning Rate Warm-up Mean?

Last updated: May 2, 2023

1. Introduction

In this tutorial, we’re going to discuss the Learning Rate Warm-up, which is a method that aims to automatically tune a hyper-parameter called Learning Rate (LR) before formally starting to train a model.

2. Context

LR Warm-up is one of the most efficient network training regularization techniques. In most situations, this method solves several problems encountered during the training of neural networks:

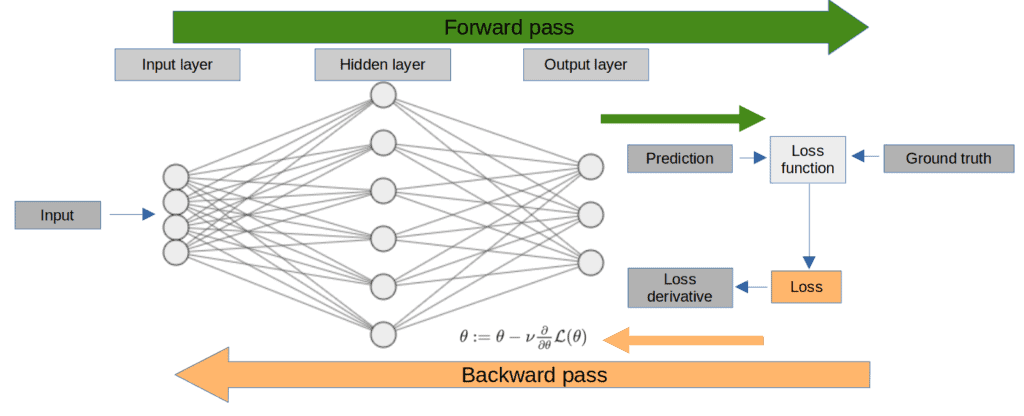
diagram

Let’s give a little context to this story. Model training requires two passes. The first pass forwards the training examples through the different layers (green arrow). Then, it calculates the loss function value. Here, only the input data and the network weights are involved.

Secondly, the backward pass (backpropagation algorithm) calculates the corresponding gradients from the loss function back to the weights of the first layer (orange arrow). During this second pass, we choose a hyper-parameter called learning rate (LR) \nu that influences how much the gradients modify the network weights at each layer:

Choosing optimal values of LR that lead to the best model performances is part of the first challenges ever discussed. Nowadays, we can adaptively adjust the LR using sophisticated adaptive strategies to ensure that a model trains well. Nevertheless, we still have to hand-pick the LR and adjust it according to the experiment results.

3. Dive Into the Learning Rate Warm-up Heuristic

Choosing an appropriate LR is a challenging task. It depends on several conditions such as hyper-parameter configuration, training data scale, the type or variant of the Gradient Descent algorithm used, and the hardware architecture (distributed system). Moreover, there may exist correlations between different hyper-parameters. Researchers showed that LR and batch size has a strong correlation. Our website also provides a tutorial describing the relationship between LR and batch size.

For most state-of-the-art architectures, starting to train with a high LR that gradually decreases at each epoch (or iteration) is a commonly adopted adaptive LR strategy. However, this adaptive LR strategy doesn’t always lead to satisfying local optima.

For example, researchers empirically demonstrated that training some Transformers models (language models such as BERT) without the LR Warm-up heuristic (depicted in figure 3 part a) leads to a higher training loss. Vaswani et al. (2017) and Popel et al. (2018) proposed to use of a small LR that gradually increases to the initial LR (called Warm-up steps) to avoid poor convergence. Priya Goyal et al. (2018) developed another warm-up scheme to train a high-performance model trained on ImageNet with large batch sizes. 

Another example is the training of Generative Adversarial Networks (GANs), which are well known for being difficult to train. A generator model and a discriminator model are competitively learning from each other in a step-by-step process. If one of these two models outperforms the other, the training fails. Frequent instabilities include gradient vanishing and mode collapse. One solution is to use the LR Warm-up on one model to balance the performance between the models.

Moreover, this heuristic also helps to stabilize training and improves generalization for adaptive stochastic optimizers such as RMSProp and Adam. Researchers showed that LR Warm-up has a regularization effect due to the gradient variance reduction.

4. Different Types of Learning Rate Warm-up Heuristics and Alternatives

There exist several types of LR warm-ups. Let’s go through some of them below:

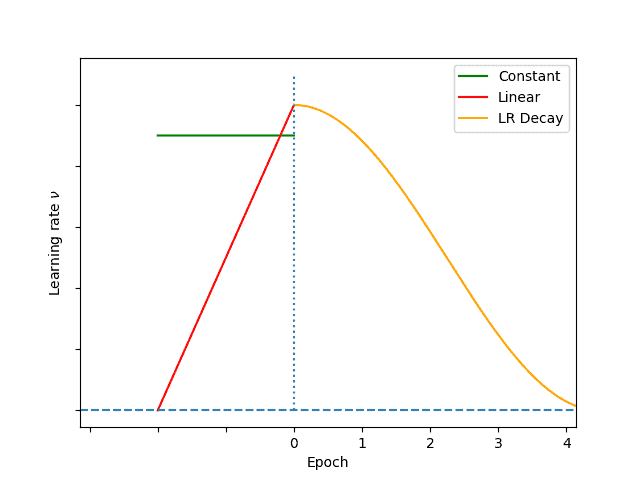
LR schedule

We denote by \nu the initial LR and w the number of warm-up steps (epochs or iterations):

  • Constant Warm-up: a constant LR value \nu_w < \nu is used to warm up the network. Then, the training directly starts with LR \nu. One drawback is the abrupt change of LR from \nu_0 to \nu
  • Gradual or linear Warm-up: the warm-up starts at LR \nu_0 and linearly increases to \nu in w steps. In other words, the LR at step j is \nu_j = \nu_0 + j\delta, \delta = (\nu - \nu_0) / (w - 1). The gradual change of LR smoothes the Warm-up by connecting \nu_0 and \nu with several intermediate LR steps

Here again, there is no method to find the most efficient LR Warm-up type other than trying them one by one with different LR values.

There are other alternatives to this heuristic such as using an optimizer called RAdam. This relatively recent optimizer provides better control of the gradient variance, which is necessary when the model trains at a high LR. RAdam detects variance instabilities and smoothly changes the LR to avoid divergence at the earliest training steps.

5. Conclusion

In this article, we discussed the Learning Rate Warm-up as a powerful network regularization technique. In most common model training, it is combined with a high LR that decreases over time, which is a standard and reliable solution to obtain a good model, including large models such as Transformers.

Comments are closed on this article!