Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
Genetic Algorithms (GAs) are powerful optimization techniques modeled on the principles of natural selection. Moreover, these tools are commonly applied across a wide range of subject fields, from engineering to finance to game designing for solving complex problems.
One of the most important operations in GA for producing the next generation is the crossover; in fact, some more types of crossovers are employed here. Partially Mapped Crossover (PMX) is one such technique.
In this tutorial, we’ll delve into the PMX and how it works.
First, let’s briefly explain what the GAs are, followed by a better understanding of why it is used. GAs belong to the family of search heuristics that simulate the natural evolution process in finding approximately the optimal solution to optimization and search problems.
Their mechanism evolves a population of potential solutions through several generations to enhance the quality of the solutions.
In the GA process, two critical genetic operators are applied to generate new offspring: mutation and crossover. Crossover is a method that mates two parents and produces one or more children. To be specific, it involves exchanging genetic material to produce improved products. One example of a crossover operator is the PMX.
In the standard single-point crossover, we randomly select a single crossover point that can be used to exchange portions of data between two or more parents. Let’s take a simple example; suppose we have two parents, P1 [1, 2, 3, 4, 5, 6, 7, 8, 9] and P2 [5, 3, 1, 8, 6, 2, 7, 4]. Firstly, let’s select the point of crossover at position 3 as follows:
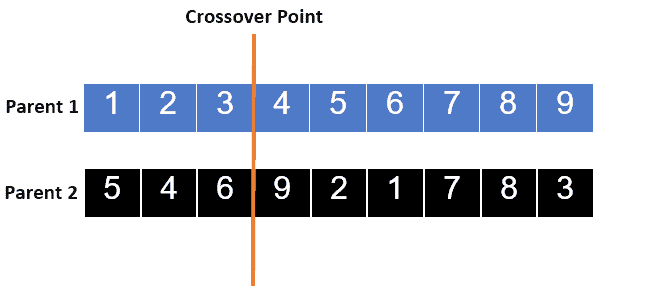
Now, we’ll exchange portions between parents to generate new offspring that migrates the features from both parents as follows:
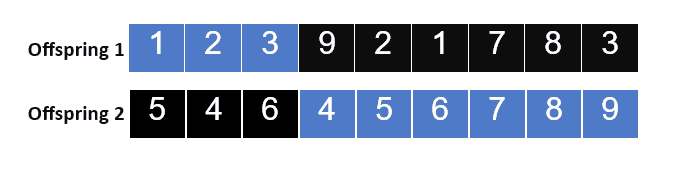
The PMX is an approach that utilizes the genetic material of the two parent solutions to propose a new offspring. The principle behind PMX is that it should preserve the arrangement of genes in a parent and allow variation in genes. PMX operates in several steps as follows:
In the case of PMX, one starts by randomly selecting two crossing points. These points divide the parents’ chromosomes into three segments: Left, middle, and right segmentation.
Firstly, copying is done to the intermediate portion among the first parents of offspring. In this, it prevents certain genes from changing with the offspring.
For each offspring, we’ll need to identify the genes on the left and right sides that need replacing. Also, we’ll establish a mapping relationship to determine their placement that should avoid gene redundancy and replace the gene from the first parent to its corresponding one in the second parent.
Based on the relationship, we’ll find and replace genes that are repeated in each chromosome.
To provide a clear insight into how PMX works, let’s suppose that we have the following two parent solutions P1 [1, 2, 3, 4, 5, 6, 7, 8, 9] and P2 [5, 4, 6, 9, 2, 1, 7, 8, 3].
We’ll select points of crossover at 3 to 6 positions as follows:
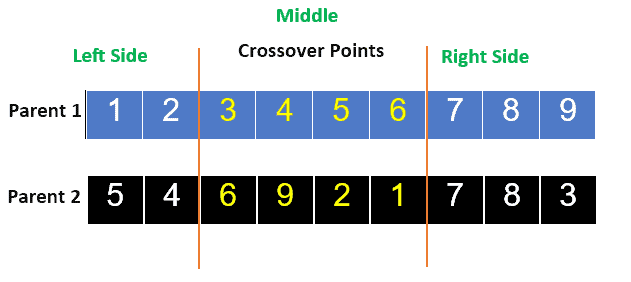
By exchanging genes from those two parents, two new offspring will be created as follows:
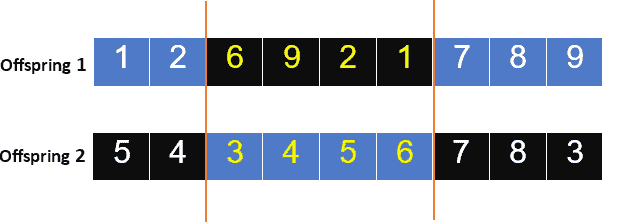
To legalize the offspring, let’s determine the mapping relationship as follows:
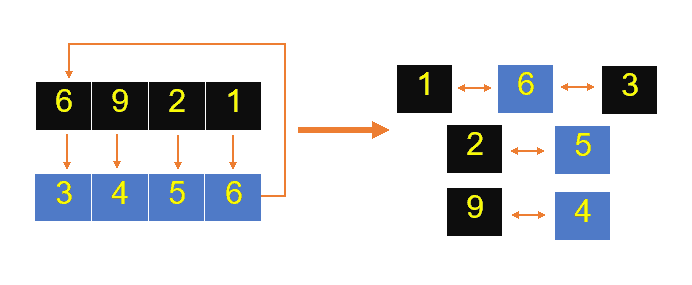
This leads to offspring that contains some genes from parents in their original order, and this maintains a middle segment with its relative identity without duplications as follows:

Partially Mapped Crossover has several advantages:
In most cases, PMX is implemented in problems that call for permutation representation, like TSP, job assignments, and so forth, in combinatorial optimization problems.
In this article, we discussed PMX as one of the most potent genetic operators that are used in GAs in solving search and optimization problems. Furthermore, PMX keeps the problem structure constant by retaining the order of genes relative to that of parent solutions and injects diversity into the problem.
The reason this technique is of great use is that it helps attain equilibrium between exploration and exploitation, which are important aspects in other fields as well. It will also enable researchers and practitioners to use GAs in solving real-world problems effectively when they understand PMX and its application.