Fibonacci Search | Baeldung on Computer Science

1. Introduction

In this tutorial, let’s study the Fibonacci search algorithm. As the name suggests, Fibonacci search algorithm is a search algorithm that involves the Fibonacci Numbers.

The Fibonacci search method, just like the Binary search method, is a comparison-based searching algorithm that is based on the divide and conquer technique. This search method works on an array that is sorted in the non-decreasing order. Before we dive deep into the internals of this search algorithm, let’s first understand the Fibonacci numbers.

2. Fibonacci Numbers

Fibonacci numbers are a sequence of numbers $\{F_n\}_{n=1}^\infty$ where any term $F_{n}$ is equal to the sum of the previous two terms i.e., $F_{n-1}$ and $F_{n-2}$ . Mathematically, we can define the Fibonacci numbers with the following recurrence equation:

$F_n = F_{n-1} + F_{n-2}$

With $F_1 = F_2 = 1$ , and conventionally defining $F_0 = 0$ .

With this knowledge, let’s generate a few Fibonacci numbers:

$F_0 = 1$

$F_1 = 1$

$F_2 = F_1+F_0 = 1+1 = 2$

$F_3 = F_2+F_1 = 2+1 = 3$

$F_4 = F_3+F_2 = 3+2 = 5$

$F_5 = F_4+F_3 = 5+3 = 8$

$...$

Fibonacci numbers play a very important role in the information coding theory that forms the backbone of wireless communication. The Fibonacci numbers are heavily used in various security coding algorithms.

3. Fibonacci Search

Now that we have developed the general background on the Fibonacci numbers, let’s understand the Fibonacci search algorithm.

3.1. General Idea Behind Fibonacci Search

Fibonacci search is a comparison-based search technique that uses Dynamic Programming. This uses the Fibonacci numbers to create a search tree and then find the key in this tree.

3.2. Fibonacci Search Algorithm

We carry out the Fibonacci search using the following steps:

To begin, we find a Fibonacci number that is greater than or equal to the size of the given array in which we have to search the $key$ . Formally, we can say that if the size of the array is $n$ then we must find a Fibonacci number $F_{k}$ such that $F_{k} \geq n$ .
The next step is to compute $F_{k-1}$ , $F_{k-2}$ , the $offset$ , and the $index$ value. The $index$ is computed using the $offset$ , $n$ , and $F_{k-2}$ .
Here, we compare the with the element at in the array. This comparison will give us one of the following three outcomes:
1. If the $key$ and array element at $index$ are equal then the $key$ is at position $index$ in the given array. We return it and stop.
2. If the $key$ is less than the array element at index $index$ , then we search the key in the left sub-tree to $F_{k-2}$ .
3. If the given $key$ is greater than the array element at $index$ , then we search the right sub-tree to $F_{k-2}$ .
If the $key$ is not found, repeat step 1 to step 5 as long as $F_{k-2} \geq 0$ i.e., we have a Fibonacci number that is greater than the length of the array $n$ .

So, we can see that after each iteration the size of array n is reduced either by $\frac{2}{3}$ or by $\frac{1}{3}$ of the array.

3.3. Pseudocode of Fibonacci Search Algorithm

In this section, let’s look into the pseudocode of the Fibonacci Search algorithm:

3.4. An Example of Fibonacci Search

Now, we’ll cement our understanding of the Fibonacci search algorithm by going through an example.

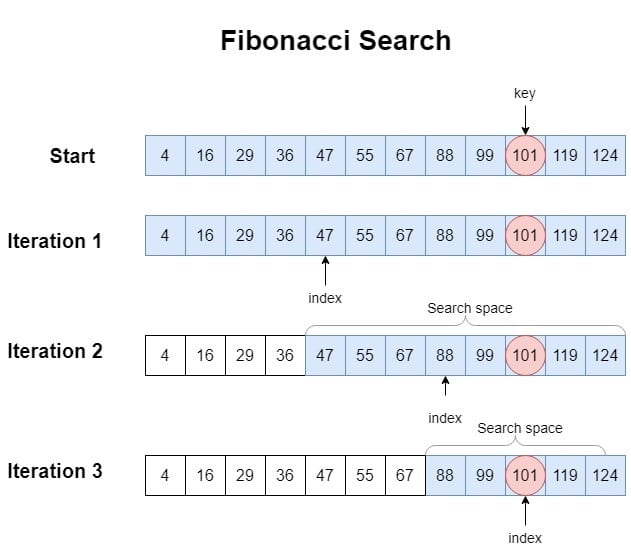
Let’s take the following sorted array $arr$ :

$4, 16, 29, 36, 47, 55, 67, 88, 99, 101, 119, 124$

From here, we invoke the Fibonacci search to find key 101.

Iteration 1: We start with full array so $n=12$ and $offset=-1$ . So, the smallest Fibonacci number $\geq$ 12 is 13. From this, we find $F_{k}=13$ , $F_{k-1}=8$ , and $F_{k-2}=5$ . Next, we compute $index=\min{(offset+F_{k-2}), n-1)}=\min((-1+5), 11)=4$ . The element at $index 4$ in $arr$ is 47. Since 101 $\geq$ 47, we move one Fibonacci number down.

Iteration 2: $F_{k}=8$ , $F_{k-1}=5$ , $F_{k-2}=3$ . We compute $index=\min{(offset+F_{k-2}), n-1)}=\min((4+3), 11)=7$ . The element at $index 7$ in $arr$ is 88. Since 101 $\geq$ 88, we move one Fibonacci number down.

Iteration 3: $F_{k}=5$ , $F_{k-1}=3$ , $F_{k-2}=2$ . We compute $index=\min{(offset+F_{k-2}), n-1)}=\min((7+2), 11)=9$ . The element at $index 9$ in $arr$ is 101. Since 101 $\eq$ 101, we return $index$ and stop.

We depict these iterations in the following figure:

4. Space and Time Complexity of Fibonacci Search

In this section, we’ll see the space and time complexity of the Fibonacci Search.

The Fibonacci Search scheme shrinks the starting search space by either two-thirds or one-third in every iteration depending upon whether the key is smaller than $F_{k-1}$ or is greater than it. Hence, we can represent it with the following recurrence relation:

$T(n) = T(\frac{2n}{3}) + T(\frac{n}{3}) + c(1)$

Let’s solve this recurrence relation.

$T(n) = T(\frac{2n}{3}) + T(\frac{n}{3}) + c(1)$

On average, the search space is reduced by $\frac{1}{3}$ , so we can take $\frac{n}{3k} = 1$ or $n=3k$ . This also implies $k=log(n)$ . Now let’s plug in $k$ for $n$ in this recurrence equation:

$T(3k) = T(2k) + T(k) + 2c(1)$

$...$

Finally, we’ll get:

$T(1) = T(\frac{k}{k}) + 2T(\frac{k}{k}) + T(\frac{k}{k}) + kc(1)$

$\boldsymbol{T(n)} = \boldsymbol{O(1)} + \boldsymbol{O(1)} + \boldsymbol{log(n)}$

Best Case: We can easily say that the best-case time complexity of the the Fibonacci search is $\boldsymbol{O(1)}$ . We’ll find this case when the search key is the first element we start comparing.
Worst Case: We can see that the worst case for the Fibonacci search method occurs when the key is always present in the larger subarray. Its worst-case time complexity is $\boldsymbol{O(logn)}$ .
Average Case: On average, we shrink the search space by $\frac{1}{3}$ , so the average case time complexity of the Fibonacci search algorithm is $\boldsymbol{O(logn)}$

Fibonacci search has $O(1)$ space complexity because no extra space other than temporary variables is used.

5. Comparison of Fibonacci Search with Binary Search

Although both the Binary search and the Fibonacci search are comparison-based searching methods that use Dynamic Programming, there are many subtle differences between them.

On average, Fibonacci Search uses $4\%$ more comparisons than Binary search. Binary Search uses division operation ( $/$ ) to divide range whereas Fibonacci Search doesn’t use $/$ albeit, it uses $+$ and $-$ .

Division and multiplication are costly operations as compared to addition and subtraction. Fibonacci Search reduces the search space by either $\frac{2}{3}$ or $\frac{1}{3}$ . On the other hand, Binary search always shrinks the search space by $\frac{1}{2}$ . Furthermore, the Fibonacci search uses $44\%$ more lookups in comparison to the Binary search algorithm.

6. Conclusion

In this article, we went through the Fibonacci search algorithm in detail.

We started by explaining Fibonacci numbers and their importance in theoretical computer science. Then, we described the Fibonacci search method by first giving its general idea. Thereafter, we explained all its steps and gave its formal pseudocode. Post that, we showcased its working with an example. We followed this discussion by calculating the space and time complexity of the Fibonacci Search. Then, we compared the Fibonacci search with the Binary search.

We conclude this article by saying that the Fibonacci search is an efficient comparison-based search technique that uses only lightweight operations such as addition and subtraction instead of heavy operations such as bit-shift, multiplication, and division.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex