1. Introduction
Euler Circuits and Paths are captivating concepts, named after the Swiss mathematician Leonhard Euler, that provide a powerful framework for analyzing and solving problems that involve networks and interconnected structures.
In this tutorial, we’ll explore the topic of Eulerian graphs, focusing on both Euler Paths and Euler Circuits, and delve into an algorithm that bears the name of Fleury, a mathematician whose work made significant contributions to this field.
2. Eulerian Graphs and Circuits
An Eulerian graph is a special type of graph that contains a path that traverses every edge exactly once. It starts at one vertex (the “initial vertex”), ends at another (the “terminal vertex”), and visits all edges without any repetition.
On the other hand, an Euler Circuit is a closed path in a graph. Like an Euler Path, it covers every edge exactly once but begins and ends at the same vertex. In this case, the initial and terminal vertex is identical.
3. Fleury’s Algorithm
Fleury’s algorithm, named after Paul-Victor Fleury, a French engineer and mathematician, is a powerful tool for identifying Eulerian circuits and paths within graphs.
Fleury’s algorithm is a precise and reliable method for determining whether a given graph contains Eulerian paths, circuits, or none at all. By following a series of steps, this algorithm methodically explores the graph, keeping track of the visited edges and, in the process, unveils the Eulerian structures hidden within.
3.1. Algorithm’s Description
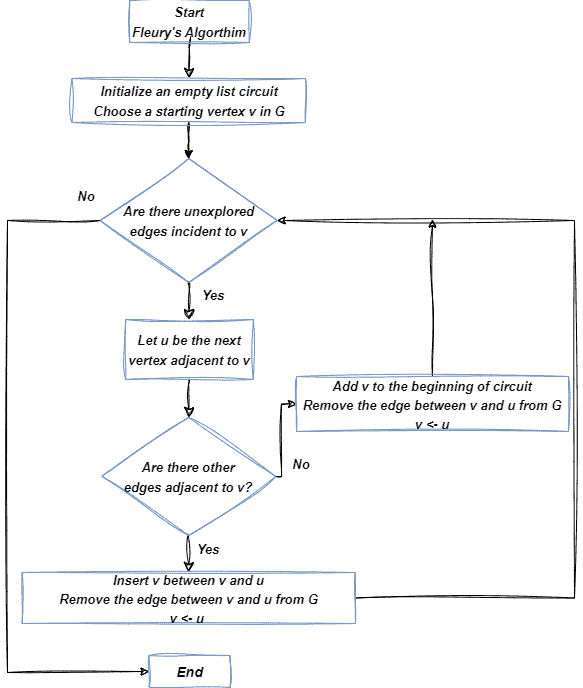
Fleury’s algorithm is a systematic method for identifying Eulerian circuits and paths in graphs. It offers a clear, step-by-step approach to uncovering the hidden structures within a graph. Before applying Fleury’s algorithm, we start with a given graph that we wish to analyze for the presence of Eulerian circuits or paths.
At first, we verify that the given graph has two or zero odd vertices. We begin from anywhere if the number of odd vertices is zero. We start at one of the two odd vertices if there are two, and take each edge one by one. When presented with an option between a bridge and something else, we always go with the non-bridge. Once we run out of edges, we stop.
Here are the key steps involved:
- Select a Starting Vertex: We begin by choosing a starting vertex in the graph. This will serve as the initial point
- Follow the Edges: Starting from the chosen vertex, we traverse an unvisited edge to an adjacent vertex. We should only follow edges that haven’t been visited yet
- Mark Visited Edges: After traversing an edge, we mark it as “visited” to ensure we don’t revisit it
- Repeat Until Stuck: We continue the process, always choosing unvisited edges, until we reach a point where we can no longer proceed without revisiting an edge. This is where the power of Fleury’s algorithm comes into play by guiding us
The flowchart of Fleury’s algorithm:
3.2. Handling Bridge Edges
A significant aspect of Fleury’s algorithm is the way it deals with bridge edges. Bridge edges are edges in a graph that, when removed, would increase the number of connected components. In the context of Eulerian circuits and paths, encountering a bridge edge can create challenges. In Fleury’s algorithm, when we encounter a bridge edge during our exploration, we should only take it if it is the only option available. Also, to ensure we can return to the starting vertex, we should store the bridge edge as a “candidate” edge, allowing us to use it later in the algorithm when necessary.
3.3. Completing the Circuit or Path
The algorithm continues until we’ve traversed all possible edges, returned to the starting vertex, or reached the desired terminal vertex.
3.4. Validity Checks
Fleury’s algorithm includes checks to verify whether a graph is Eulerian. If, at any point during the algorithm, we discover that there are unvisited edges in the graph, it means there’s no Eulerian path or circuit. In such cases, we won’t be able to return to the starting vertex or reach the desired terminal vertex, indicating the absence of a solution.
3.5. Complexity
Fleury’s algorithm is generally efficient, especially when the graph is dense or contains a large number of edges. Its time complexity is typically , where
is the number of edges in the graph. While it may not be the fastest algorithm for every scenario, its simplicity and reliability make it a valuable choice for many practical applications.
3.6. Pseudocode of Fleury’s Algorithm
The pseudocode of Fleury’s algorithm:
The result is stored in the circuit list, which will contain the vertices in the order they should be traversed to form the Eulerian circuit or path.
4.
Let’s consider a simple graph to demonstrate Fleury’s algorithm. This graph contains four vertices and four edges, and our objective is to find an Eulerian circuit if one exists.
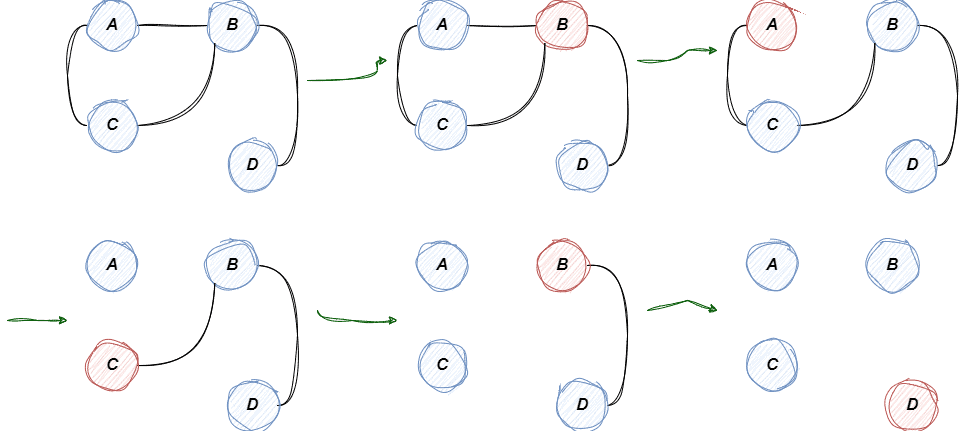
We can begin pathways from any of the two odd-degree vertices, “” and “
,” which are both accessible.
Now let’s begin our walk at vertex ‘‘. Vertex ‘
‘ has three edges that go from it. Since there is a bridge there and we can’t return to “
“, we don’t choose the edge “
–
.” Any of the two remaining edges will do. Assume we choose “
–
.” We go to vertex “
” after removing this edge. We select the only edge from vertex “
,” erase it, and proceed to vertex “
.” The Euler tour is now called “
–
–
.”
Once more, vertex has only one edge, so we choose that, eliminate it, and go to vertex “
“. The Euler tour is now called “
–
–
–
–
.”
This is where we finish because there are no more edges to be found. The tour “–
–
–
–
” is the final one.
5. Comparison with Other Methods
Fleury’s algorithm, while reliable, may not always be the fastest option. It competes with other algorithms for finding Eulerian paths and circuits. Its efficiency shines in dense graphs, but for sparse graphs, Hierholzer’s algorithm might be faster. Other algorithms, like the Depth-First Search (DFS) method, offer additional options for solving similar problems, each with its advantages and use cases. Choosing the most suitable method depends on the specific characteristics of the graph and the problem at hand.
6. Applications and Limitations
Euler Paths and Circuits, along with Fleury’s algorithm, find their way into practical applications across various domains.
In logistics and transportation, finding efficient delivery routes can be akin to solving an Eulerian path problem. Fleury’s algorithm, if applicable, ensures that a delivery vehicle visits each street once before returning to the depot. This minimizes travel time and resource use.
In electrical engineering, Eulerian circuits are instrumental in designing circuits where every component connection is visited exactly once. Fleury’s algorithm aids in creating optimized circuit layouts, reducing errors and redundancies.
Fleury’s algorithm is also employed in genomics for sequencing DNA fragments. By identifying Eulerian paths in DNA sequences, scientists can reconstruct the original genetic information efficiently.
However, it’s essential to acknowledge that Fleury’s algorithm has its limitations. It might not apply in cases where a graph doesn’t adhere to Euler’s Theorem, such as graphs with more than two vertices of odd degree. Additionally, for graphs with millions of edges, the time complexity may be impractical.
7. Conclusion
In this article on Euler Circuits and Paths, we’ve uncovered the essence of Fleury’s algorithm and its real-world applications. Understanding the importance of Eulerian graphs and their efficient traversal using Fleury’s algorithm is crucial for diverse problem-solving.
As we conclude, it’s noteworthy that the field of graph theory is evolving. Prospective advancements may introduce more efficient algorithms and broaden the scope of Eulerian paths and circuits. Advances in computation and algorithms are poised to tackle larger, complex challenges.