The Dining Philosophers

1. Overview

In this tutorial, we’ll discuss one of the famous problems in concurrent programming –  the dining philosophers – formulated by Edgar Dijkstra in 1965. He presented the problem as a demonstration of the problem of resource contention. It occurs when computers need to access shared resources.

2. The Problem Definition

We can see the setup for the problem in the figure below. As we’ve seen, five philosophers are sitting around the table. They live in a house together. There are also five forks on the table between each philosopher.

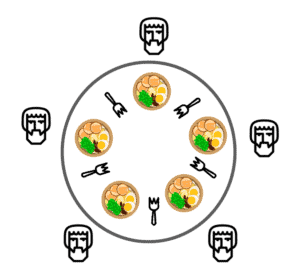
When they think they don’t need any forks. However, assuming the complexity of their food, they have to use two forks, both the one on their right and the one on their left, when they eat. The disagreement, or in other words, contention for these forks, makes this problem important in concurrent programming.

3. Characteristics of the Problem

The first solution that comes to mind is locking each fork with a mutex or a binary semaphore. However, even if we guarantee that no two neighbors are eating simultaneously, this solution may lead to deadlock because all the five philosophers can get hungry simultaneously. In this situation, all of them will grab the fork on their left, and from that moment, no one will access the fork on their right. The philosophers are stuck.

To clarify the problem and give a formal description, Dijkstra proposes three states, let’s say , where implicates a philosopher is thinking, implicates a philosopher is hungry, implicates a philosopher is eating.

We can say that there is a basic loop for each philosopher. They will eat and think through the states , and so on.

Let’s summarize the other specific characteristics of the problem:

• As we’ve said, a philosopher will need left and right forks to eat food
• Only one philosopher can hold each fork at a certain period, and so a philosopher can use the fork only if another philosopher is not using it
• Philosophers need to put down forks after they finish eating so that forks become available for others
• Also, a philosopher can only get the fork on their right and the one on their left if they are available
• Philosophers cannot start eating before getting both forks
• The problem assumes that there is endless supply and demand so that there is no limit to how much food or stomach space can exist

4. Solution

Of course, there is more than one solution to this problem, but we’re going to look at the original one, which is based on Dijkstra’s solution and changed by Tanenbaum. We’ll share the critic functions in the pseudocode format.

This solution uses one mutex, one semaphore per philosopher, and one state variable per philosopher, which we explained in the previous section.

We have a state array to keep track of every philosopher’s state, whether they’re hungry or not. Also, there are other constant variables to simulate the dining philosophers problem:

As mentioned earlier, we have one mutex to make thread-safe our critical sections, which are our forks and states of philosophers for this problem. And one semaphore for each philosopher:

Our philosophers have a cycle right where they think and eat forever. So, here is the routine that we need to do.  variable indicates the philosopher number:

4.1. Preventing the Deadlock

At this point, we need to carefully decide whether a philosopher is able to eat or not. To do that, imagine we have a waiter who is responsible for telling the philosophers whether they can eat now or they should wait:

For example, philosopher 1 is hungry and starts eating before all of them. And then, philosopher 2 will ask the waiter whether she is allowed to eat or not. The waiter says go and check. She tries to take forks first. However, since both forks are not available, she’ll need to wait.

After philosopher 1 finishes eating, we call the put_forks() and the check() functions to make available the forks for other philosophers:

The check() functions inside take_forks() and put_forks() functions will prevent the deadlock.

Finally, let’s look at the eat() and think() methods that our philosophers enjoy doing during their lifetime:

These two functions just print the information about which philosopher thinks or eats. It also puts the philosopher threads to sleep at random duration:

5. What Can Be Wrong?

We’ve already discussed that we can have a deadlock situation when we don’t adjust the necessary synchronization primitives.

Starvation is another issue that we need to consider when developing concurrent programs. Resource starvation may happen if any philosopher cannot take both forks because of a timing problem.

These problems can occur when multiple processes need access to shared resources. These topics generally are studies in concurrent programming. Dijkstra did a great job of coming up with a problem analogous to such difficulties in real computer systems.

6. Conclusion

In this article, we’ve given the description and the solution to the dining philosophers. It’s analogous to resource contention problems in computing systems and proposed by the Dijkstra. We’ve also discussed the important synchronization problems such as deadlock and how to prevent it in the scope of the dining philosophers.

Furthermore, we can check the Java implementation of the dining philosophers problem.