1. Introduction
In this tutorial, we’ll go through the practical applications of the directed acyclic graph. It finds several interesting uses in scientific and computational applications.
We’ll examine the properties of this mathematical structure and understand what makes it widely useful.
2. What Is a Directed Acyclic Graph?
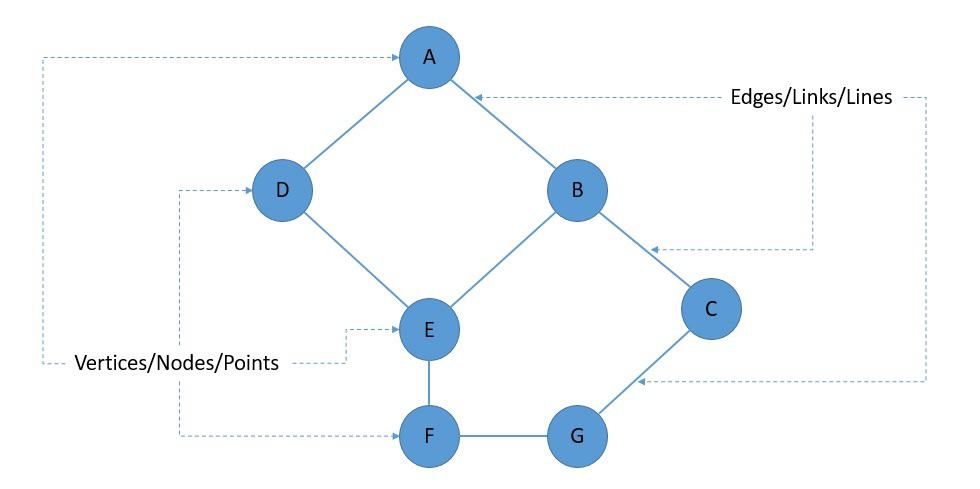
For those of us uninitiated in this area, a directed acyclic graph is basically a specific type of graph. A graph is a mathematical structure used to model pairwise relations between objects. These objects are known as vertices, nodes, or points. Further, these relations are known as edges, links, or lines:
Now, an edge can have a direction, wherein we say that the edge links the two vertices asymmetrically. This gives us what we know as a directed graph. Conversely, if an edge links the two vertices symmetrically, or in other words, does not have a direction, it gives us an undirected graph:
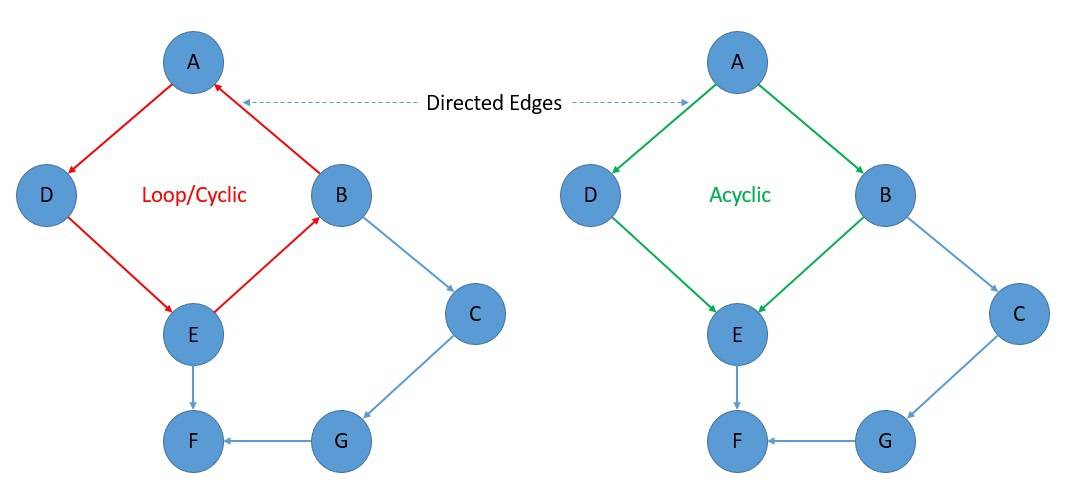
Further, if we’ve got a directed graph, and we’re able to follow the edges from one node to another without forming a loop, we can say that we’ve got a directed acyclic graph or a DAG. In mathematical terms, a directed graph is a DAG if and only if it can be topologically ordered.
3. Properties of DAG
Graph theory, a branch of mathematics, defines several properties of DAGs. For instance, reachability relation, transitive closure, transitive reduction, and topological ordering. It can be interesting to understand them better to see why DAGs are useful.
Reachability is the ability to get from one node to another within a graph. In order theory, another branch of mathematics, we can reason about the reachability of a DAG using its partial order relations. It’s a useful tool for analyzing DAGs.
Formally, a binary relation on a set is a partial order if and only if it is reflexive, anti-symmetric, and transitive. If we consider all nodes in a DAG as part of a set, its partial order gives us the set ordered by the reachability of the graph.
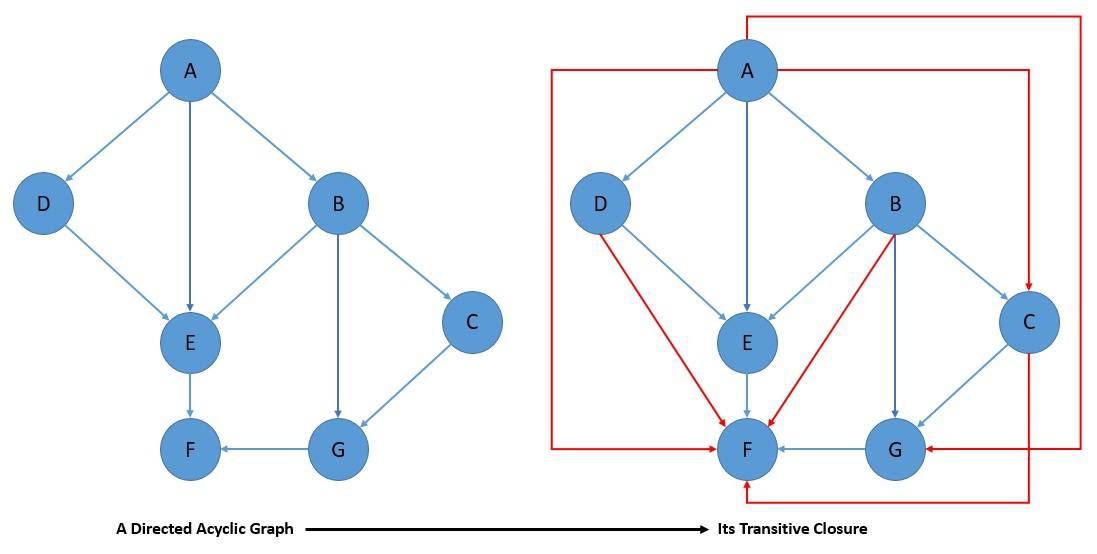
The transitive closure of a DAG is another graph with the same set of nodes and as many edges as possible, retaining the reachability relation of the original graph:
The transitive reduction of a DAG is yet another graph with the same set of nodes and as few edges as possible, retaining the reachability relation of the original graph:
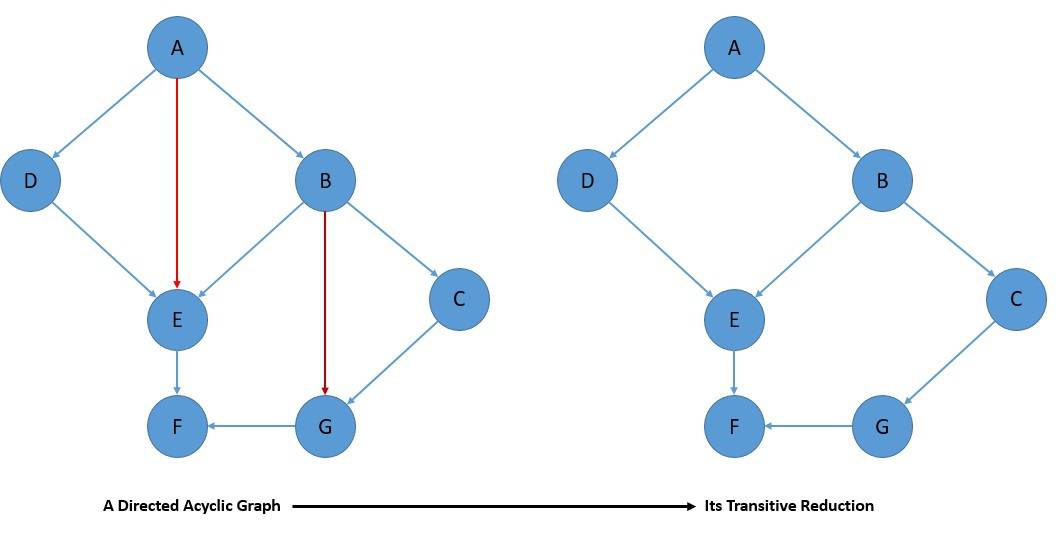
Effectively, it’s the opposite of transitive closure. All transitive reductions of a graph share the same transitive closure. Transitive closure and reduction form important tools for understanding the reachability relations of a DAG.
The topological ordering of a directed graph is the ordering of its nodes into a sequence. In such a sequence, for every edge, the start node of the edge occurs earlier in the sequence than its end node:
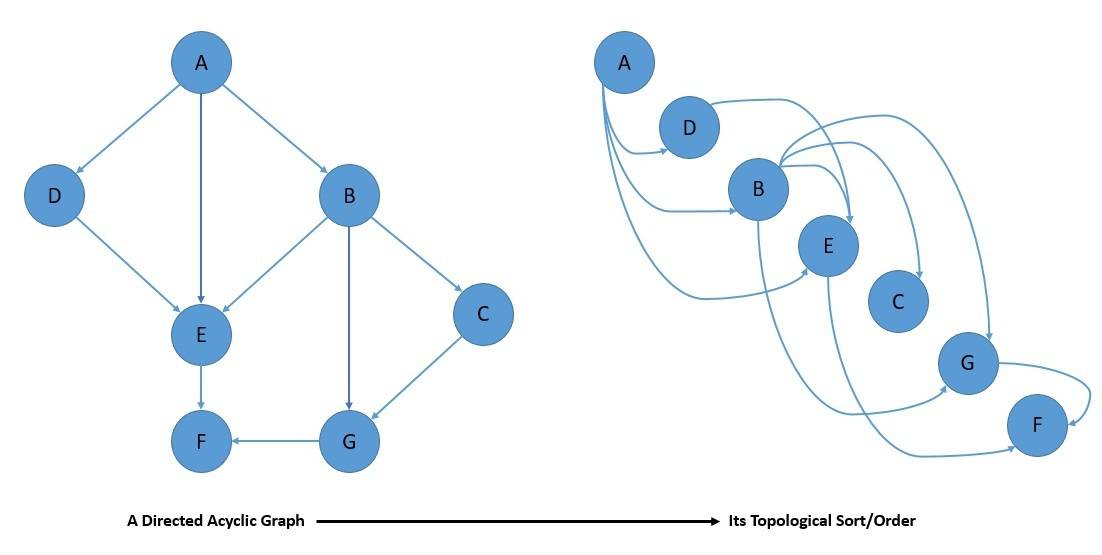
Now, every graph with a topological ordering is acyclic. Hence, every DAG has at least one topological ordering. Interestingly, the topological ordering of a DAG also gives us linear extensions of partial orders, which effectively provides reachability relations of the DAG.
4. Practical Applications of DAG
Due to their interesting properties, DAGs are useful in several practical applications. These include applications in biology, information science, and computing. While it’s difficult to cover exhaustively, we’ll focus on the practical applications of the DAG in some of the popular fields of study.
4.1. Data Processing
In a typical data processing network, a series of computations are run on the data to prepare for one or more ultimate destinations. We can use a DAG to represent this network of data processing elements. Here, the data enters a processing element or vertex through its incoming edges and leaves the element through its outgoing edges:

Representing a data processing flow using DAG helps in clearly organizing various steps and the associated order of these computations. An interesting property of the DAG and the data processing flow it represents is that there can be multiple paths in the flow. This helps recognize the need to process data in multiple ways to accommodate different outputs and needs.
There are quite a number of practical data processing networks that we can imagine representing using DAG. A language compiler represents straight-line code with a DAG describing the inputs and outputs of each arithmetic operation performed within the code. This allows the compiler to perform common subexpression elimination efficiently.
4.2. Scheduling
Scheduling refers to the problem of assigning work to be done in a system in a manner that optimizes the overall performance while ensuring the correctness of the result. It’s interesting to note that many scheduling problems have ordering constraints. Depending upon the number of parameters, even a modest-looking problem can become a very difficult problem to solve.
We can represent a scheduling problem using a weighted directed acyclic graph. Let’s take the example of a task scheduling problem. Here, a vertex can represent the task and its weight can represent the size of the task computation. Similarly, an edge can represent the communication between two tasks and its weight can represent the cost of communication:
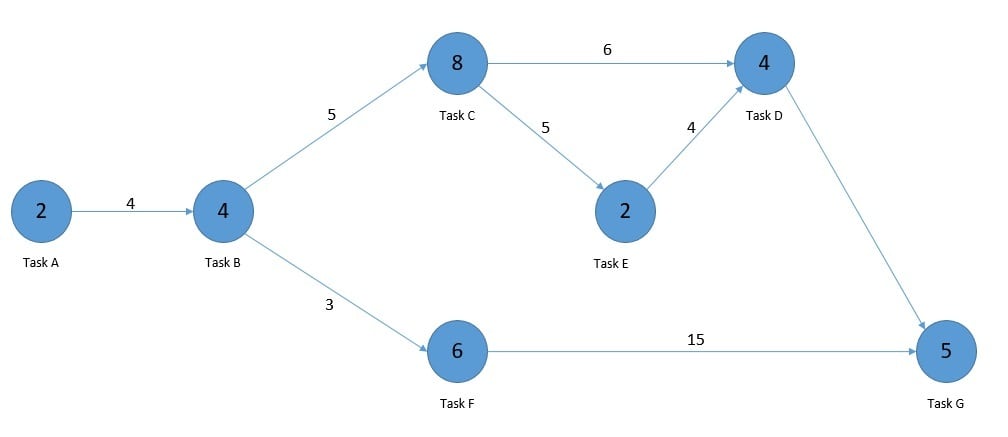
One such scheduling problem with the application of DAG is the program evaluation and review technique (PERT). This is basically a method for the management of large projects and makes use of DAG for representation and finding the critical path. There are several other real-life scheduling problems like airline routing & scheduling and assembly line scheduling.
4.3. Other Practical Applications
Genealogy or family chart represents the family relationships in a conventional tree structure. We can represent them as a DAG with a vertex for each family member and an edge for each parent-child relationship. It can get very complex and has importance in the field of medicine and social work.
Distributed revision control systems maintain the version history of computer programs in a distributed manner. These are usually represented as a DAG with a vertex representing each revision and edges connecting pairs of revisions that were directly derived from each other.
Citation graphs are directed graph in information science that describes the citations within a collection of documents. Here, we represent a document in the collection with a vertex and the citations to the documents with edges in the graph. This forms an important tool in citation analysis.
Bayesian networks are a probabilistic graphical model that represents a set of variables and their conditional dependencies. A DAG is an intuitive choice for representing such networks. These are useful for analyzing one of the several possible causes for the occurrence of an event.
Data compression is the process of encoding information using fewer bits than the original representation. A DAG finds unconventional use here for compact representation of a collection of sequences by representing the shared subsequences within these sequences.
5. DAG in Data Engineering Products
We have seen that DAG is quite useful in representing and solving several problems. It’s not possible to cover all such applications in detail in this tutorial. However, we’ll cover some of these applications of DAG in popular and open-source data engineering products.
5.1. Apache Spark
Apache Spark is an open-source engine for large-scale data processing with implicit data parallelism and fault tolerance. At the core of Spark architecture lies the resilient distributed dataset (RDD). RDD is basically a fault-tolerant collection of elements distributed over a cluster of machines.
We can process the elements of RDD in parallel with fault tolerance. Interestingly, the workflow of the data processing within Spark is managed as a DAG. Here, the vertices represent the RDDs, and the edges represent the operation to be applied to RDD.
Consequently, every edge directs from earlier to later processing in the sequence. Once we submit our code to Spark, it interprets and converts it to a DAG or operator graph. Next, the DAG Scheduler picks up the operator graph on the call of action and splits it into stages of the task:
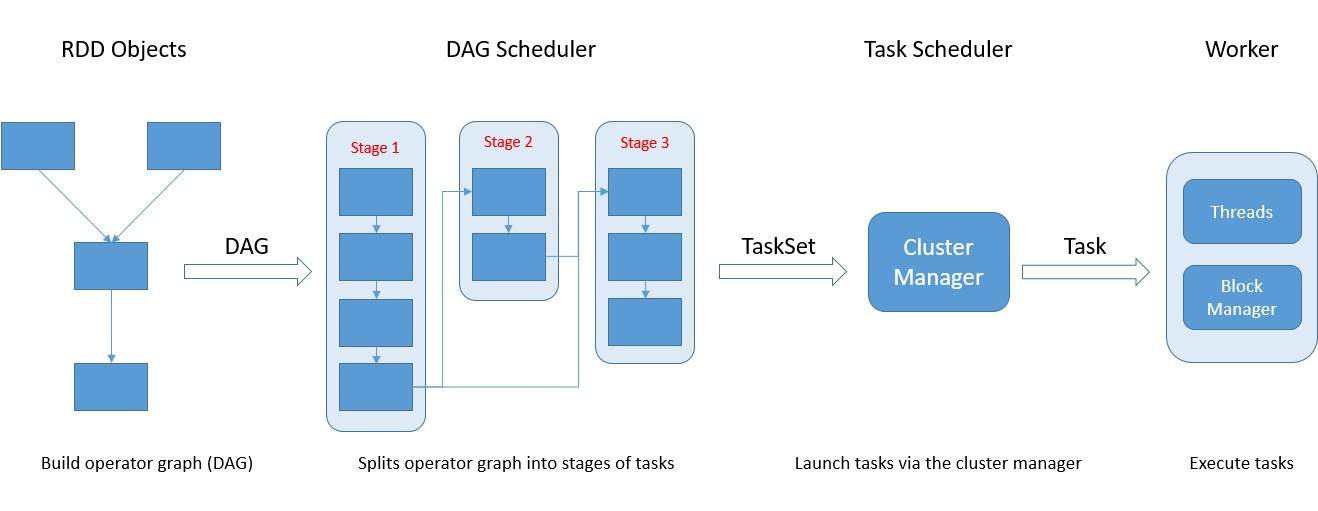
A stage basically contains the task based on the partition of the input data. The scheduler is also responsible for pipelining the operators together in a stage for greater efficiency. Finally, the Task Scheduler picks up these stages and launches them through the cluster manager.
Spark was a significant improvement over the limitations of Hadoop. One of the key differences was in their execution model. While Hadoop MapReduce relies on a two-step execution process, Spark creates a DAG to schedule the tasks. This helps Spark optimize the global execution plan.
Moreover, the DAG execution model also helps Spark achieve fault tolerance. Basically, RDD is split into multiple partitions, and each worker node operates on a specific partition. On failure of a node, a new node can resume the specific tasks on a specific partition using the DAG.
5.2. Apache Storm
Apache Storm is an open-source distributed real-time computation system. It can reliably process unbounded streams of data doing real-time processing. At the core of Storm architecture lies the Storm topology, which is basically a graph of spouts and bolts connected with stream groupings.
Let’s understand some of these terminologies. A stream is an unbounded sequence of tuples that are processed in parallel in a distributed fashion. A spout is a source of the stream in the topology. All processing, like filtering and joins in the topology, happens in bolts.
Topology is what brings all of these together in Storm. Part of the topology is to define the streams that each bolt should receive as input. A stream grouping defines how that stream should be partitioned among the bolt’s tasks:
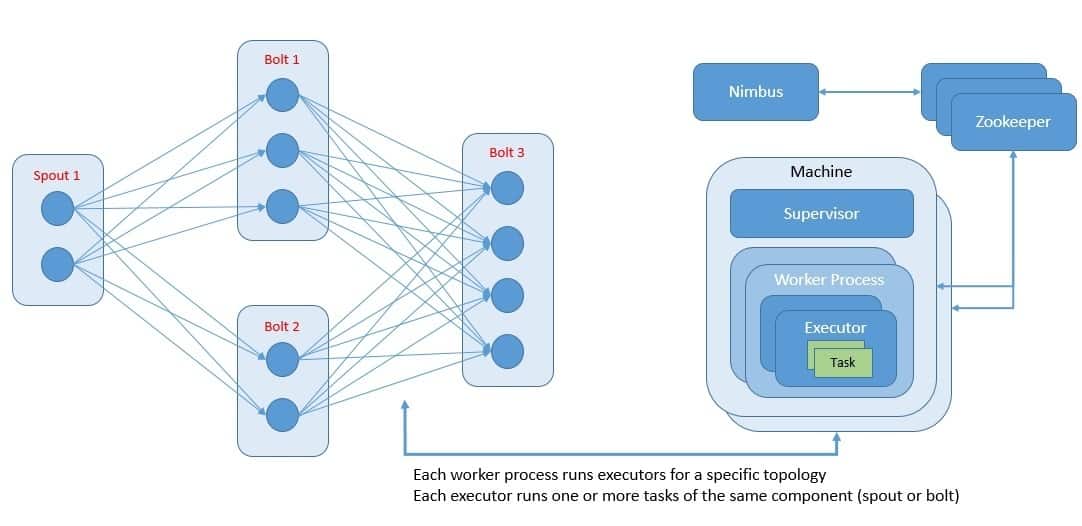
Interestingly, topologies in Storm are designed as a DAG. Here, the spouts and bolts in the topology act as the vertices in the graph. Edges in the graph are streams and direct data from one node to another. When brought together as DAG, the topology acts as the data transformation pipeline.
Topology definitions in Storm are basically Thrift structs that are deployed onto a cluster using Nimbus, which is a Thrift service. The cluster consists of worker processes that execute a subset of a topology. A running topology consists of many processes running on many machines within the cluster.
Storm guarantees that every tuple of data will be fully processed, also known as an at-least-once processing guarantee. One of the key enablers for this promise is the DAG-based topology. It allows Storm to track the lineage of a tuple as it makes its way through the topology efficiently.
5.3. Apache Airflow
Apache Airflow is an open-source platform to programmatically author, schedule, and monitor workflows. Airflow workflows are basically configuration-as-code written in Python, allowing for dynamic pipeline generation. It’s possible to extend the platform with custom operators and executors.
A workflow in Airflow is represented as a DAG and contains individual pieces of work called tasks. Tasks are arranged in the DAG with dependencies and data flows taken into account. The DAG also helps to define the order in which to execute the tasks and run retries.
A scheduler is responsible for triggering scheduled workflows and submitting the tasks to the executor to run. An executor handles the running tasks typically by pushing them to workers. This all comes with an intuitive user interface to inspect, trigger, and debug the behavior of DAGs and tasks:
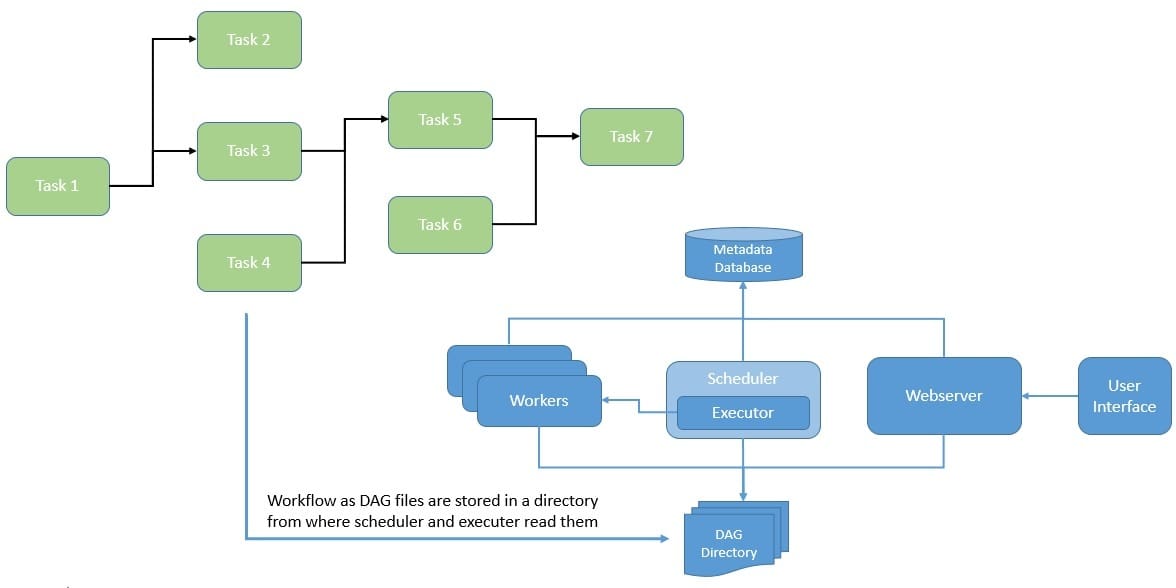
Tasks within a DAG in Airflow can be of three types – Operators, Sensors, and a TaskFlow-decorated task. Operators are basically predefined tasks, while Sensors are a special subclass of Operators meant to wait for external events. The last one is a way to package custom Python functions as tasks.
DAGs in Airflow is designed to run many times, and multiple runs of them can happen in parallel. Further, DAGs are parametrized, which includes an interval they should be running for. Tasks have dependencies on each other, which makes up the edges in the graph.
Interestingly, DAGs can get very complex, so Airflow provides mechanisms like SubDAGs to make them sustainable. These basically allow us to make reusable DAGs that we can embed in other DAGs. There is also the concept of TaskGroups to visually group tasks in the UI.
6. Conclusion
In this tutorial, we understood the basic concepts and nature of a directed acyclic graph. Further, we went through some of the practical applications of DAG in solving real-life problems.
Lastly, we covered some of the popular open-source products that use DAG in their architecture.