SAT and 3-SAT - Cook-Levin Theorem | Baeldung on Computer Science

1. Overview

The Boolean Satisfiability Problem or in other words SAT is the first problem that was shown to be NP-Complete. In this tutorial, we’ll discuss the satisfiability problem in detail and present the Cook-Levin theorem.

Furthermore, we’ll discuss the 3-SAT problem and show how it can be proved to be NP-complete by reducing it to the SAT problem.

2. Introduction to SAT

In this section, we’ll discuss a general definition of the SAT problem.

A given boolean expression, determining if there exists a truth assignment to its variables for which the expression is true is defined as the satisfiability problem.

Let’s take an example to discuss further.

We’ve taken two expressions here. To test whether there exists a truth assignment to variables $a$ , $b$ , $c$ , we’ve tested all possible assignments.

There are $\mathsf{5}$ satisfying truth assignments for the expression $(a \wedge b) \vee c$ above and hence it is satisfiable.

But the expression $(a \wedge \neg a) \vee (c \wedge \neg c)$ is false for all possible truth assignments and hence it is unsatisfiable.

This takes $\mathcal{O}(2^3)$ . This is called the truth table method. If there are $n$ variables in the boolean expression, then the truth table method would take $\mathcal{O}(2^n)$ time to determine if there is a truth assignment that makes the expression true.

3. Conjunctive Normal Form (CNF)

When we’re discussing the SAT problem, it’s essential to know about the conjunctive normal form (CNF). In this section, we’ll see a short description of the CNF concept.

A boolean expression is said to be in CNF form if it’s a conjunction of a set of clauses, where each clause is defined as a disjunction (logical OR) of literals. We can define a literal as a variable or a negation of a variable. In the above example $a, \neg a, b, \neg b, c, \neg c$ are all literals.

Every boolean expression can be expressed as a CNF by repeatedly using De Morgan’s Laws, the law of double negation and distributive laws under AND and OR:

$C_1 \wedge C_2 \wedge ... \wedge C_n$

where,

$C_i = a_1^i \vee a_2^i \vee ... \vee a_k^i$

The above CNF is a $k$ -CNF, that is, it has a maximum of $k$ literals in every clause. We pick each literal from a set of $m$ variables:

$x_1, x_2,...,x_m, \neg x_1, \neg x_2,..., \neg x_m$

4. SAT Variants

There are a number of SAT variants. In this section, we’ve listed out few.

4.1. 2-SAT

In the 2-SAT problem, every clause has two literals and is solvable in a polynomial-time problem.

We can pick a variable $a$ , and then assign true. We assign true to the other variable of all the clauses with $\neg a$ . If those clauses are satisfied, then we pick the remaining clauses which don’t have $a$ or $\neg a$ and continue the process.

On the other side, if the clauses with $\neg a$ are not all satisfied at this point, then we assign false to $a$ and repeat the above process. If all the clauses containing $a$ and $\neg a$ are all not satisfied, then the 2-SAT is unsatisfiable.

An important application of 2-SAT is to identify an undirected graph that can be represented as a complete bipartite graph and independent set. This helps to identify the business relationships among autonomous subsystems of the internet.

Many algorithms for the automatic label placement problem use the 2-SAT concept.

4.2. Weighted 2-SAT

Given a CNF with $\mathsf{2}$ literals per clause and an integer $k$ , the problem of determining if there is a truth assignment with at most $k$ variables set to true for which the CNF is satisfiable.

This problem is NP-Complete. Many algorithms use the weighted 2-SAT concept for solving the vertex cover problem.

4.3. 3-SAT

In the 3-SAT problem, each clause has at most $\mathsf{3}$ literals. This problem is NP-Complete.

The 3-SAT problem is part of the Karp’s 21 NP-complete problems and is used as the starting point to prove that the other problems are also NP-Complete. One example is the independent set problem. The Independent Set Problem can be shown to be NP-Complete by showing that the 3-SAT is polynomially reducible to an independent set problem.

4.4. Exactly One 3-SAT

Each clause in the 3-SAT problem has at least $\mathsf{1}$ literal that must be true. But in Exactly one 3-SAT problem, we determine if the CNF is satisfiable where exactly one of the three literals in every clause is true and the other two are false. This problem is NP-Complete.

Exactly one 3-SAT is a known NP-Complete problem, and it’s used in reduction to prove other problems NP-complete.

5. Cook-Levin Theorem

In this section, we’ll discuss the Cook-Levin theorem which shows how to prove that the SAT is an NP-Complete problem.

The statement of Cook-Levin theorem is the boolean satisfiability problem is NP-complete.

For a given truth assignment, we can verify if the CNF or boolean expression is satisfiable or not in polynomial time.

If a decision problem can be verified in polynomial time by a deterministic Turing machine, then it can be solved in polynomial time by a non-deterministic algorithm. Proof of this statement can be found in multiple textbooks.

SAT is in NP if there is a non-deterministic Turing machine that can solve it in polynomial time.

If any problem in NP can be reduced to an SAT problem in Polynomial-time, then it’s NP-Complete. We can prove by taking any language $\L \in NP$ and reducing it to SAT in polynomial time. Because $L \in NP$ , there exists a verifier $V$ which can verify the decision problem $L$ in polynomial time.

Let $w$ be an input on which verifier $V$ checks if the output is a yes or a no or ( $\mathsf{1}$ or $\mathsf{0}$ ). Because $V$ works in polynomial time, at every time step, the algorithm makes the hardware affect a constant number of memory units.

After $t$ time steps, the algorithm affects $t$ memory units. We can represent each of these operations at every time step using AND, OR, NOT logical gates. Hence it is possible to build a circuit in polynomial for any language $L \in NP$ . This would be a polynomial time in the number of bits present in input $w$ .

The decision problem $L$ now reduces to determining if there is an input $w$ for which the circuit built above outputs $1$ (true). The CNF equivalents of AND, OR, and NOT gates are shown below. This reduction is done using De Morgan’s laws, material implication, and double negation.

Let’s start with AND gate. Let $a$ , $b$ be the inputs, $x$ be the output:

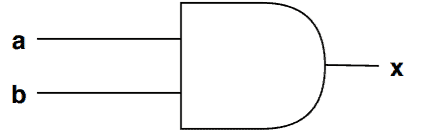
The functionality of the above AND gate in CNF form is:

$x \iff (a \wedge b)$

$(x \implies (a \wedge b)) \wedge ((a \wedge b) \implies x)$

$(\neg x \vee (a \wedge b)) \wedge (\neg(a \wedge b) \vee x)$

$(\neg x \vee a) \wedge (\neg x \vee b) \wedge (\neg a \vee \neg b \vee x)$

For OR gate, let $a$ , $b$ be the inputs, $x$ be the output:

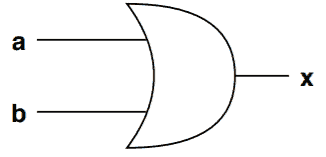
The functionality of the above OR gate in CNF form is:

$x \iff (a \vee b)$

$(x \implies (a \vee b)) \wedge ((a \vee b) \implies x)$

$(\neg x \vee (a \vee b)) \wedge (\neg(a \vee b) \vee x)$

$(\neg x \vee a \vee b) \wedge (\neg a \vee \neg b \vee x)$

For NOT gate, let $a$ be the input, $x$ be the output:

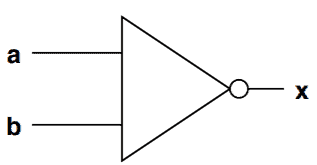
The functionality of the above NOT gate in CNF form is:

$a \iff \neg x$

$( \neg x \implies a ) \wedge (a \implies \neg x)$

$(a \vee x) \wedge (\neg a \vee \neg x)$

From the above gates, we can observe that we can convert the circuit into an equivalent CNF form.

Hence all NP-Hard problems can be reduced to CNF, which means, they can be reduced to an SAT problem. Hence the SAT is NP-Complete.

6. Introduction to 3-SAT

3-SAT defines the problem of determining whether a given CNF, with each clause containing at most $3$ literals, is satisfiable or not.

The 3-SAT problem is simpler then 2-SAT as it seeks to solve the 2-SAT problem where there can be at most three variables in each parenthesis in the boolean expression. Still, there is no polynomial-time algorithm exists for 3-SAT.

Let’s see an example. We’ll take an SAT problem and make it a 3-SAT.

We’re taking an example of an SAT problem:

$\phi = (x_1 \vee x_2 \vee \neg x_4 \vee \neg x_5) \wedge (\neg x_1 \vee x_4 \vee x_5 \vee \neg x_6) \wedge (x_6 \vee x_7) \wedge (\neg x_2 \vee x_3)$

$\phi$ is satisfiable for truth values:
$x_1 = 1$ , $x_2 = 0$ , $x_3 = 0$ , $x_4 = 1$ , $x_5 = 0$ , $x_6 = 0$ , $x_7=1$

We can introduce two new variables $y_1, y_2$ to make the given SAT problem to a 3-SAT problem:

$\phi^\prime = (x_1 \vee x_2 \vee y_1) \wedge ( \neg y_1 \vee \neg x_4 \vee \neg x_5) \wedge (\neg x_1 \vee x_4 \vee y_2) \wedge ( \neg y_2 \vee x_5 \vee \neg x_6) \wedge (x_6 \vee x_7) \wedge (\neg x_2 \vee x_3)$

$\phi^\prime$ is satisfiable for truth values $x_1 = 1$ , $x_2 = 0$ , $x_3 = 0$ , $x_4 = 1$ , $x_5 = 0$ , $x_6 = 0$ , $x_7=1$ , $y_1 = 0$ , $y_2 = 0$ . In fact, for either values of $y_1$ and $y_2$ , the 3-CNF is satisfiable.

7. NP-Completeness of 3-SAT

In this section, let’s see how we can prove that 3-SAT is NP-Complete.

We can convert any problem $L \in NP$ into an SAT problem in polynomial time. That is, we can express it as a boolean formula and can convert every boolean formula into its corresponding CNF form.

SAT to 3-SAT reduction takes polynomial time. That is the corresponding CNF to 3-CNF takes polynomial time. Let the CNF representation of the original SAT problem is:

$\phi = C_1\wedge C_2 \wedge ... \wedge C_n$

where $\phi$ is satisfiable if every clause $C_i$ is satisfiable.

Without loss of generality, let’s assume that the clause $C_r$ has more than $\mathsf{3}$ literals:

$C_r = (a_1 \vee a_2 \vee ... \vee a_m),\ m >3$

where each $a_i$ is picked from a set of literals:

$x_1, x_2,...,x_m, \neg x_1, \neg x_2,..., \neg x_m$

Let

$A = a_3 \vee a_4 \vee ... \vee a_m$

$C_r = a_1 \vee a_2 \vee A$

Define $C_r^\prime$ as following:

$C_r^\prime = (a_1 \vee a_2 \vee y) \wedge (\neg y \vee A)$

where $y$ is a new variable and we introduce it to make a clause with $3$ literals. This same procedure can be applied repeatedly to the second clause in $C_r^\prime$ until there are no more clauses with more than three literals remaining.

Now we need to prove that $C_r^\prime$ and $C_r$ are equisatisfiable.

For case 1 we need to show $C_r^\prime$ is satisfiable, then $C_r$ is satisfiable. Let’s start this proof:

$C_r^\prime$ is satisfiable, then $C_r$ is satisfiable

$\implies (a_1 \vee a_2 \vee y)=1,\ (\neg y \vee A) =1$

if $y=0:$

$C_r^\prime = (a_1 \vee a_2 \vee 0) \wedge (1 \vee A)$

$= (a_1 \vee a_2) \wedge (1)$

(1) $\begin{equation*}(a_1 \vee a_2) = 1 \end{equation*}$

if $y=1:$

$C_r^\prime = (a_1 \vee a_2 \vee 1) \wedge (0 \vee A)$

(2) $\begin{equation*}(A) = 1 \end{equation*}$

For either values of $y$ , for $C_r^\prime$ to be satisfiable, either $(a_1 \vee a_2) = 1$ or $(A) = 1$ . From (1) and (2), we can say that $C_r = 1$ if $C_r^\prime =1$ .

If $C_r$ satisfiable, then $C_r^\prime$ is satisfiable.

If either $a_1 = 1$ or $a_2 = 1$ , then we can assign $y=0$ and $C_r^\prime =1$ because:

$C_r^\prime = (a_1 \vee a_2 \vee 0) \wedge (1 \vee A)$

and one or both of $a_1, a_2$ are $1$ .

If $a_1 =0, a_2=0$ , then $A=1$ . By assigning $y=1$ , we can make $C_r^\prime$ satisfiable.

Using the above procedure, $C_r \forall\ r$ where the number of literals is greater than $\mathsf{3}$ can be converted into clauses with at most $\mathsf{3}$ variables that are equisatisfiable. From the above proof, we can see that this takes polynomial time in the number of literals in every clause.

Therefore, we can reduce the SAT to 3-SAT in polynomial time. From Cook’s theorem, the SAT is NP-Complete. Hence 3-SAT is also NP-Complete.

8. Conclusion

In this tutorial, we’ve presented a detailed discussion of the SAT problem. We’ve discussed the Cook-Levin theorem to show SAT is an NP-Complete problem.

Furthermore, we’ve given a short introduction to the 3-SAT problem and showed a reduction of SAT to 3-SAT.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex