Algorithms to Check if a Linked List Is a Circular Linked List

1. Introduction

In Computer Science, a linked list is a linear data structure in which a pointer in each element determines the order.

In this tutorial, we’ll show how to check if a linked list is a circular linked list.

2. Circular Linked List 

Each element of a linked list contains a data field to store the list data and a pointer field to point to the next element in the sequence. We can use a pointer to point to the start element of a linked list:

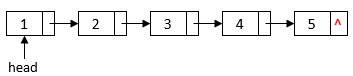
In a regular linked list, the last element has no next element. Therefore, its pointer field is . However, in a circular linked list, the last element has a reference to one of the elements in the list:

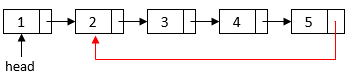
3. Hash Table Solution

It is easy to see that if a linked list contains a cycle, we’ll eventually visit the same node twice when we traverse the linked list. Therefore, we can use a hash table to solve this problem:

algorithm isCircularList(head):
    // INPUT
    //     head = first element of a linked list
    // OUTPUT
    //     true if the linked list is circular, otherwise false

    hashTable <- construct empty hash table
    currentNode <- head

    while currentNode != null:
        if hashTable contains currentNode:
            return true
        else:
            add currentNode into hashTable

        currentNode <- currentNode.next

    return false

This algorithm traverses the linked list and records each node’s reference in a hash table.  We use a linked list node’s reference as its unique identifier. If we see the same reference again in the hash table, we can return to indicate a circular linked list. Otherwise, we’ll finally reach the node and return .

Let’s assume each hash table operation, such as insertion and searching, takes time. Then, this algorithm’s overall time complexity is as we traverse the whole linked list only once. The space complexity is also , as we need to store all the nodes into the hash table.

4. Solution With Two Pointers

To detect whether a linked list is a circular linked list, we can use two pointers with different speeds: a pointer and a pointer. We use these two pointers to traverse the linked list. The pointer moves one step at a time, and the pointer moves two steps.

If there is no cycle in the list, the pointer will eventually reach the last element whose pointer is and stop there.

For a circular linked list, let’s imagine the and pointers are two runners racing around a circular track. At the beginning, the runner passes the runner. However, it’ll eventually meet the runner again from behind. We can use the same idea to detect if there is a cycle in the linked list:

algorithm isCircularList(head):
    // INPUT
    //     head = first element of a linked list
    // OUTPUT
    //     true if the linked list is circular, otherwise false

    if head is null:
        return false

    slow <- head
    fast <- head.next

    while slow != fast:
        if fast is null or fast.next is null:
            return false

        slow <- slow.next
        fast <- fast.next.next

    return true

In this algorithm, we first have a sanity check on the input pointer. Then, we start two pointers, and , at different locations. In the loop, we advance the two pointers at different speeds. If the pointer reaches the terminated pointer, we can conclude that the linked list does not have a cycle. Otherwise, the two pointers will eventually meet. Then, we finish the loop and return to indicate a circular linked list.

5. Complexity Analysis of the Two-pointer Solution

If the linked list doesn’t have a cycle, the loop will finish when the pointer reaches the end. Therefore, the time complexity is in this case.

For a circular linked list, we need to calculate the number of steps to make the pointer catch the pointer. Let’s first break down the movement of the pointer into two stages.

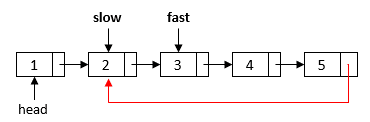
In the first stage, the pointer takes steps to enter the cycle. At this point, the pointer has already in the cycle and is elements apart from the pointer in the linked list direction. In the following example, the distance between the two pointers is 3 elements since we need to advance the pointer 3 elements to catch the pointer in the cycle:

In the second stage, both pointers are in the cycle. The pointer moves 2 steps in each iteration, and the pointer moves 1 step. Therefore, the pointer can catch up 1 element in each iteration. Since the distance between these two pointers at the beginning is , we need iterations to make these two pointers meet.

Therefore, the total running time is , where is the number of elements between the and the start element of the cycle, and is the distance between the two pointers when the pointer reaches the cycle. Since is at most the cycle length, the overall time complexity is also .

The space complexity is  as we only use two pointers ( and ) in the algorithm.

6. Conclusion

In this tutorial, we showed a sample circular linked list. Also, we discussed two linear-time algorithms that can check if a linked list is a circular linked list.