Serialize and Deserialize a Binary Tree

1. Introduction

Serialization is translating a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network. In the future, we can deserialize the sequence to reconstruct the same data structure or object.

In this tutorial, we’ll introduce algorithms to serialize and deserialize a binary tree.

2. Binary Tree Definition

A binary tree is a hierarchal data structure in which each node has at most two children. Each node of a binary tree has 3 elements: a data element to hold the node data and two children pointers to point its left and right children. If a child node does not exist, we use  to represent that:

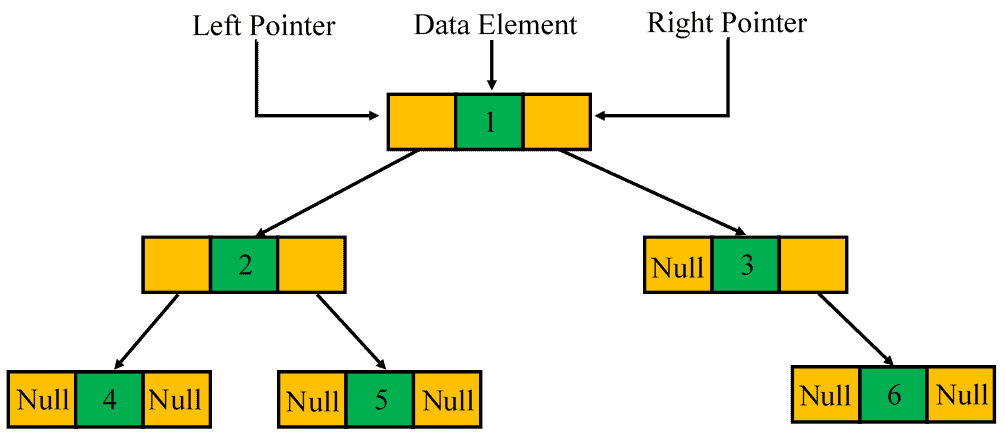
There are 3 main binary tree traversal methods: pre-order, in-order, and post-order. We can serialize and deserialize a binary tree with a combination of two methods, e.g., pre-order and in-order methods.

In this tutorial, we’ll show how to serialize and deserialize a binary tree with a single tree traversal method. For example, we can serialize a binary with pre-order traversal and deserialize it with the same method.

3. Serialize a Binary Tree with Pre-order Traversal

We can use the pre-order traversal algorithm to serialize a binary tree. In a pre-order binary tree traversal, we traverse the root node first. Then, we traverse its left and right subtrees, respectively. For example, we can pre-order traverse the above example tree in the order: .

When we serialize the tree, we also consider the nodes. In this case, we can use to represent a node. Therefore, the pre-order sequence becomes: .

We can use a recursive pre-order traversal algorithm to construct the serialization sequence:

algorithm serializePreOrder(root, sequence):
    // INPUT
    //    root = the root node of the binary tree
    //    sequence = the sequence to append the serialization result
    // OUTPUT
    //    A serialization sequence of the binary tree

    if root is null:
        sequence <- sequence + "#"
    else:
        sequence <- sequence + root.data
        serializePreOrder(root.left, sequence)
        serializePreOrder(root.right, sequence)

In this algorithm, we first serialize the node data, then recursively serialize its left and right children. If we meet a node, we also serialize it with a special character .

If the binary tree contains nodes, the overall running time of this algorithm is since we visit each node only once. The space requirement is also to store the serialization sequence. Although we need extra space to store the nodes in the serialization sequence, the extra space is at most because each node has at most two children.

4. Deserialize a Binary Tree with Pre-order Traversal

We can use the same pre-order algorithm to deserialize a sequence into a binary tree:

algorithm deserializePreorder(sequenceIterator):
    // INPUT
    //    sequenceIterator = an iterator for the serialization sequence
    // OUTPUT
    //    The root node of the deserialized binary tree

    if not sequenceIterator.hasNext():
        return null
    data <- sequenceIterator.next()
    if data = "#":
        return null
    else:
        root <- create a new tree node with data
        root.left <- deserializePreorder(sequenceIterator)
        root.right <- deserializePreorder(sequenceIterator)
        return root

algorithm deserialize(sequence):
    // INPUT
    //    sequence = the serialization sequence of a binary tree
    // OUTPUT
    //    The root node of the deserialized binary tree

    sequenceIterator <- create an iterator for sequence
    return deserializePreorder(sequenceIterator)

For the simplicity of algorithm description, we use an iterator object of the serialization sequence as the input of the recursive function. Different programming languages have similar iterator support. For example, we can use an Iterator interface in Java.

The deserialization process is similar to the serialization process. We first deserialize the root node data, then recursively deserialize its left and right children. If we see a special character , we deserialize it as a node.

The overall running time and space requirement are both since we construct each node only once.

5. Serialize a Binary Tree with Post-order Traversal

Similar to the pre-order traversal, we can use use the post-order traversal algorithm to serialize a binary tree. In a post-order binary tree traversal, we first traverse its left and right subtrees respectively. Then, we visit the root node at last.

We can use a recursive post-order traversal algorithm to construct the serialization sequence:

algorithm serializePostOrder(root, sequence):
    // INPUT
    //    root = the root node of the binary tree
    //    sequence = the sequence to append the serialization result
    // OUTPUT
    //    A serialization sequence of the binary tree

    if root is null:
        sequence <- sequence + "#"
    else:
        serializePostOrder(root.left, sequence)
        serializePostOrder(root.right, sequence)
        sequence <- sequence + root.data

In this algorithm, we first recursively serialize the left and right children. Then, we serialize the root node data in the end. The overall running time and space requirement are also .

6. Deserialize a Post-order Traversal Sequence

In the pre-order serialization, we put the root node at the beginning of the sequence. However, we put the root node at the end of the sequence in a post-order serialization. For example, we can post-order traverse the example tree in the order: . Therefore, the post-order traversal is a kind of reverse operation of the pre-order traversal.

To serialize a post-order traversal sequence, we can first reverse the sequence and then use a modified pre-order deserialization process to build the binary tree:

algorithm deserializePostorder(sequenceIterator):
    // INPUT
    //    sequenceIterator = an iterator for the reversed serialization sequence
    // OUTPUT
    //    The root node of the deserialized binary tree

    if not sequenceIterator.hasNext():
        return null
    data <- sequenceIterator.next()
    if data = "#":
        return null
    else:
        root <- create a new tree node with data
        root.right <- deserializePostorder(sequenceIterator)
        root.left <- deserializePostorder(sequenceIterator)
        return root

algorithm deserialize(sequence):
    // INPUT
    //    sequence = the serialization sequence of a binary tree
    // OUTPUT
    //    The root node of the deserialized binary tree

    sequence <- reverse the sequence
    sequenceIterator <- create an iterator for the reversed sequence
    return deserializePostorder(sequenceIterator)

In the post-order traversal, we traverse the tree in the order:

• left subtree
• right subtree
• root node

Since our deserialization process works in a backward order, we deserialize the root node first. Then, we deserialize the right subtree. Finally, we deserialize the left subtree. 

The overall running time and space requirement are both since we construct each node only once.

7. In-order Traversal Binary Tree Serialization and Deserialization

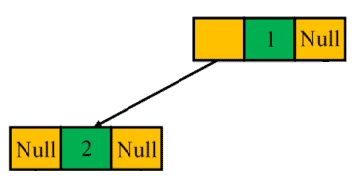
We cannot use the in-order tree traversal method to serialize and deserialize a binary tree. In an in-order binary tree traversal, we traverse the left subtree first. Then, we visit the root node and traverse the right subtree. This traversal makes it hard to locate the root node in the serialized sequence.

For example, an in-order traversal of the following binary tree can produce a sequence: :

However, we can produce the same in-order sequence on the following binary tree:

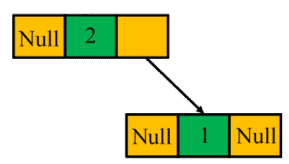
Therefore, we cannot deserialize an in-order sequence back to a binary tree as the related tree is not unique.

8. Conclusion

In this tutorial, we showed two algorithms, pre-order traversal and post-order traversal, to serialize and deserialize a binary tree. We also showed that the in-order traversal algorithm is not suitable for binary tree serialization and deserialization.

Finally, we confirmed that all serialization and deserialization algorithms have linear time and space complexity.