Calculating the Height of a Binary Tree | Baeldung on Computer Science

1. Overview

In this tutorial, we’ll learn how to find the height of a binary tree, and look at an example.

Number of Nodes in a Binary Tree With Level N

Learn how to calculate the minimum and maximum number of nodes in binary trees

Serialize and Deserialize a Binary Tree

Learn algorithms to serialize and deserialize a binary tree

Getting a Path From a Root to a Node in a Binary Tree

A quick and practical guide to getting a path from a root to a node in a binary tree.

2. Definition

First, let’s start by defining the height of a binary tree.

The height of a node in a binary tree is the largest number of edges in a path from a leaf node to a target node. If the target node doesn’t have any other nodes connected to it, the height of that node would be $\mathsf{0}$ . The height of a binary tree is the height of the root node in the whole binary tree. In other words, the height of a binary tree is equal to the largest number of edges from the root to the most distant leaf node.

A similar concept in a binary tree is the depth of the tree. The depth of a node in a binary tree is the total number of edges from the root node to the target node. Similarly, the depth of a binary tree is the total number of edges from the root node to the most distant leaf node.

One important observation here is that when we calculate the depth of a whole binary tree, it’s equivalent to the height of the binary tree.

3. Example

Let’s take a binary tree:

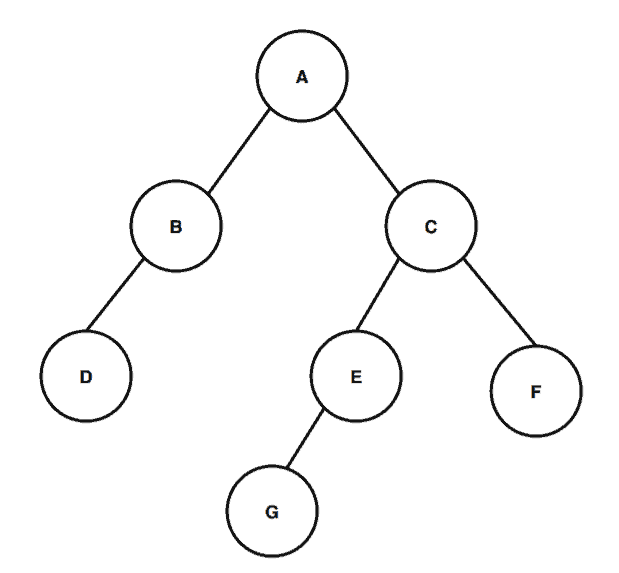
First, we’ll calculate the height of node $C$ . So, according to the definition, the height of node $C$ is the largest number of edges in a path from the leaf node to node $C$ . We can see that there are two paths for node $C$ : $C \rightarrow E \rightarrow G$ , and $C \rightarrow F$ . The largest number of edges among these two paths would be $\mathsf{2}$ ; hence, the height of node $C$ is $\mathsf{2}$ .

Now we’ll calculate the height of the binary tree. From the root, we can have three different paths leading to the leaf nodes: $A \rightarrow C \rightarrow F$ , $A \rightarrow B \rightarrow D$ , and $A \rightarrow C \rightarrow E \rightarrow G$ . Among these three paths, the path $A \rightarrow C \rightarrow E \rightarrow G$ contains the largest number of edges, which is $\mathsf{3}$ . Therefore, the height of the tree is $\mathbf{3}$ .

Next, we want to find the depth of node $B$ . We can see that from the root, there’s only one path to node $B$ , and it has one edge. Thus, the depth of node $B$ is $\mathsf{1}$ .

As we previously mentioned, the depth of a binary tree is equal to the height of the tree. Therefore, the depth of the binary tree is $\mathbf{3}$ .

4. Algorithm

In the previous sections, we defined the height of a binary tree. Now we’ll examine an algorithm to find the height of a binary tree:

algorithm BTHeight(root):
    // INPUT
    //     root = the root node of the binary tree
    // OUTPUT
    //     returns the height of the binary tree

    if root = null:
        return 0

    leftTHeight <- BTHeight(root.left)
    rightTHeight <- BTHeight(root.right)

    return max(leftTHeight, rightTHeight) + 1

We start the algorithm by taking the root node as an input. Next, we calculate the height of the left and right child nodes of the root. If the root doesn’t have any child nodes, we return the height of the tree as $\mathsf{0}$ .

Then we recursively call all the nodes from the left and right subtree of the root node to calculate the height of the binary tree. Finally, once we calculate the height of the left and right subtree, we take the maximum height among both and add one to it. The number returned by the algorithm would be the height of the binary tree.

5. Time Complexity Analysis

As a best case scenario, we would have only one node in the binary tree. In such a case, we would only execute the first condition of the algorithm when the root is null, and return the height of the tree as $\mathsf{0}$ . Here, the time complexity would be $\mathbf{\mathcal{O}(1)}$ .

In general, we calculate the height of each node in the tree. We call all the nodes recursively, calculate the height of the left and right subtree from the root node, and finally, return the height of the whole binary tree. Thus, we visit all the nodes in the tree.

Let’s suppose that the number of nodes in a binary tree is $n$ . Therefore, the time complexity would be $\mathbf{\mathcal{O}(n)}$ .

6. Conclusion

In this article, we discussed how to calculate the height of a binary tree. We presented a recursive algorithm, and analysis of the time complexity required for the algorithm.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex