1. Introduction
In this tutorial, we’ll test a few open-source solvers for mixed integer programming.
2. Benefits of Mixed Integer Solvers
In mixed integer programming (MIP), we optimize an objective function that has at least one integer argument. For example:
(1) 
Solving MIP problems can be demanding. We use specialized solvers to find their optimal solutions. Ready-to-use solvers offer several benefits:
- MIP solvers are suitable for solving problems in many fields since many real-world problems can be modeled as MIP problems
- MIP solvers are designed to find optimal solutions
- Some MIP solvers are scalable, which means they are efficient in handling large-scale optimization problems with many decision variables and constraints
- MIP solvers are robust. They are capable of handling a wide variety of problem types
- MIP solvers can be integrated with other tools
- MIP solvers can be used in a variety of applications, such as scheduling, logistics, finance, engineering, and more
- MIP solvers can be used to make better decisions by providing a clear understanding of the trade-offs between different variables
Using an off-the-shelf solver means we don’t have to code them from scratch, which saves time. However, with many solvers available, it’s hard to choose or even identify the best one.
3. Which Solvers Will We Test and How?
We focus on three commonly used free and open-source MIO solvers:
- GLPK (GNU linear programming kit) is capable of solving large-scale linear, integer, mixed-integer, and related problems. GLPK uses the simplex method for solving linear problems and branch-and-bound for dealing with integer optimization problems
- COIN-OR (Computational Infrastructure for Operations Research) is a C++ software that provides a suite of high-capacity tools for operations research. Its COIN-OR CBC tool solves mixed integer problems
- PuLP (Python Linear Programming) includes several MIO solvers. PuLP is written in Python and uses a branch-and-bound algorithm to optimize objective functions
3.1. Performance Metrics
We’ll evaluate each solver on a benchmark instance of problem instances, running every solver on every instance ten times. In doing so, we’ll record the optimality gap and solving time. The former is the relative difference between the found and optimal values:
(2) 
We calculate the optimality gap as the difference between the objective value of the best-known feasible solution (or current solution) and the optimal objective value (i.e., best bound). The solving time is the time a solver takes to produce an output.
To account for statistical fluctuations and randomness, we’ll compare the solvers using the median gaps and their median deviations since medians are less sensitive to outliers than means.
3.2. Benchmark Instance
We used the following standard benchmark instances consisting of:
- bnatt400:
variables and 
constraint - bnatt500:
variables and 
constraint - neos-631710:
variables and 
constraint - neos5:
variables and constraint
Additionally, we evaluated the solvers on Equation (1) while varying the problem size.
We used the default settings of each solver in Python.
3.3. Need for Varying Problem Size
Evaluating MIP solvers on different problem sizes serves several purposes, including:
- to study the complexity characteristics of the optimization problem and each solver’s behavior
- comparing MIP solver’s performances across different problem sizes allows for benchmarking different solvers
- it helps to analyze the performance of the solver in terms of computational time and efficiency across different problem sizes
- it allows us to assess the solver’s scalability
4. Comparison
Let’s check the results.
4.1. Solver’s Performances on Problem Size
We added to Equation (1) a generic linear constraint of the form:
(3) 
where size is the problem size because increasing it makes the search space larger.
As the problem size increases, the solution time for each solver shows a non-monotonic behavior. Both COIN-OR CBC and PuLP have a sharp increase up to around a size of 50, after which their solving time varies within more or less the same interval:
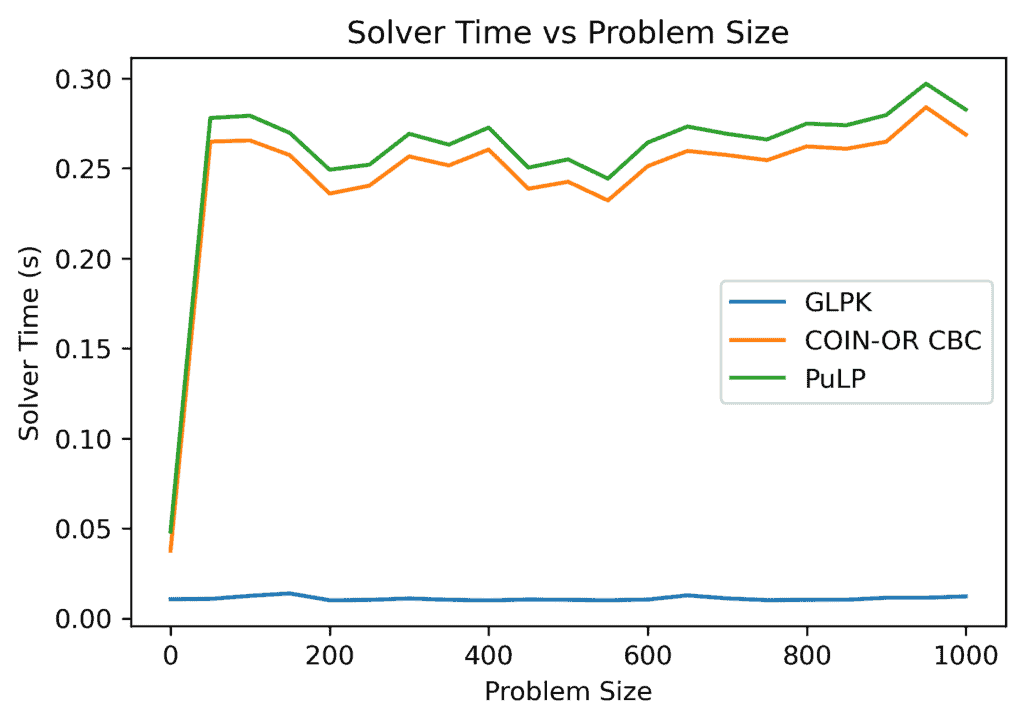
GLPK shows a stable behavior with a deviation of around 
seconds and was also the fastest. COIN-OR CBC and PuLP were slower than GLPK and had comparable performances to one another.
4.2. Performance on Benchmark Instances
All the solvers found the optimal solution in all the runs.
When it comes to time, each solver’s time varies on the instance:
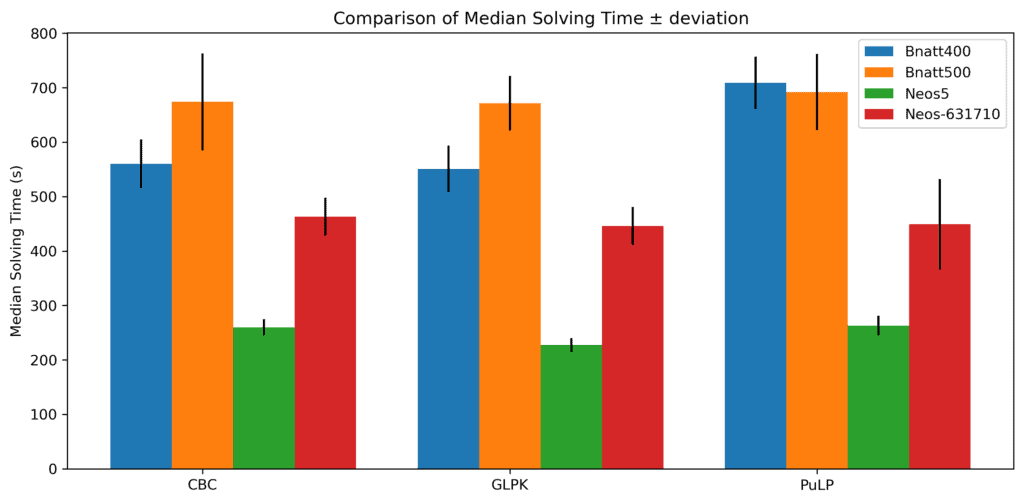There doesn’t seem to be a significant difference in median times (
median absolute deviations).
However, we can see that their deviations differ in the cases of bnatt500 and neos-631710. PuLP shows more time variability on the latter, while its variability is roughly the same as for CBC on the former. In general, if the median solving times are similar for a bunch of solvers, we prefer the one whose time is variable the least.
5. Choosing the Best Solver
Let’s summarize the results:
Overall, GLPK outperformed other solvers on our custom example in terms of solving time. The solvers’ overall performances on the four benchmark instances are approximately the same.
However, using different benchmarks or different optimization formulations might lead to other results.
6. Conclusion
In this article, we described some open-source mixed integer optimization solvers. These solvers are suitable for solving problems in many areas due to their accuracy and scalability. We compared three open-source solvers: GLPK, COIN-OR CBC, and PuLP. There is no clear winner, although GLPK was the fastest on our custom example.