How to Project a 3D Point Onto a 2D Plane? | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll explain how to project a three-dimensional point onto a (two-dimensional) plane with its coordinate system.

2. Setup

Let’s say we have a point with coordinates $Z=[z_1, z_2, z_3]$ and a plane whose equation is:

(1) $\begin{equation*} a x_1 + b x_2 + c x_3 = d \qquad (a, b, c, d \in R, \quad a^2 + b^2 + c^2 \neq 0, \quad x_1, x_2, x_3 \in R) \end{equation*}$

where $[x_1, x_2, x_3]$ is any point in the plane, and $a, b, c, d$ are its parameters. Geometrically, $[a, b, c]$ is the vector normal to the plane. It doesn’t have to be unitary but needs to be non-zero. Parameter $d$ is the $x_3$ -coordinate of the plane’s intersection with the $x_3$ -axis. Visually:

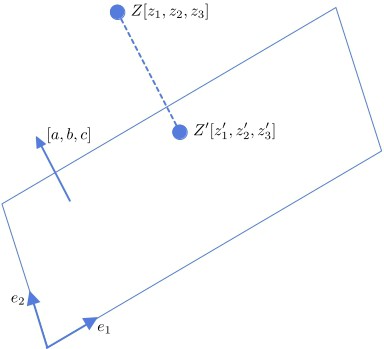
The plane has a two-dimensional coordinate system of its own, defined by two base unit vectors $e_1$ and $e_2$ .

So, our goal is to find the coordinates of the $\boldsymbol{Z}$ ‘s projection $\boldsymbol{Z'}$ onto the plane in the coordinate system defined by $\boldsymbol{e_1}$ and $\boldsymbol{e_2}$ .

3. How to Project a Point

Let’s start by projecting $Z$ onto the plane and finding the coordinates in the original 3D system. Since the projection $\boldsymbol{Z'}$ belongs to the plane, its coordinates fit Equation (1):

(2) $\begin{equation*} a z_1' + b z_2' + c z_3' = d \end{equation*}$

Further, the line connecting $\boldsymbol{Z}$ and $\boldsymbol{Z'}$ is perpendicular to the plane, so it’s parallel to the plane’s normal vector. The line’s vector is $[z_1' - z_1, z_2' - z_2, z_3' - z_3]$ . So, the following should hold:

(3) $\begin{equation*} \begin{aligned} z_1' - z_1 &= k a \\ z_2' - z_2 &= k b \\ z_3 '- z_3 &= k c \end{aligned} \end{equation*}$

for some real number $k$ .

By solving (3) for $z_1'$ , $z_2'$ , and $z_3'$ , and plugging the obtained expressions into Equation (2), we get:

$\begin{aligned} a(z_1 + k a) + b(z_2 + k b) + c( z_3 + k c) &= d \\ a z_1 + b z_2 + c z_3 + k(a^2 + b^2 + c^2) & = d \\ k = \frac{d - a z_1 - b z_2 - c z_3}{a^2 + b^2 + c^2} \end{aligned}$

If the normal vector is also a unit vector (i.e., its length is 1), the denominator is also one since it denotes the vector’s squared length.

By substituting $k$ in Equations (2), we can easily calculate the coordinates:

$\begin{aligned} z_1' &= z_1 + k a \\ z_2' &= z_2 + k b \\ z_3' &= z_3 + k c \end{aligned}$

3.1. Example

Let $Z=[1, 0, 0]$ and let the plane’s equation be:

$x_1 + 3 x_2 + 3 x_3 = 20$

For $k$ , we get:

$k = \frac{20 - 1}{1 + 9 + 9} = \frac{19}{19} = 1$

So, the projection $Z'$ is $[1 - 1, 0 - 3, 0 - 3] = [0, -3, -3]$ .

3.2. An Alternative Parameterization of the Plane

The plane can be specified by the normal vector $[a, b, c]$ and a point $X_0=[p, q, r]$ in it. For an arbitrary point $X=[x_1, x_2, x_3]$ in the plane, it must hold that the vector $X - X_0=[x_1 - p, x_2 - q. x_3 - r]$ is perpendicular to $[a, b, c]$ :

Therefore:

$\begin{aligned} a(x_1 - p) + b(x_2 - q) + c(x_3 - r) &= 0 \\ a x_1 + b x_2 + c x_3 - ap - bq - cr & = 0 \\ a x_1 + b x_2 + c x_3 &= ap + bq + cr \end{aligned}$

This is the same as Equation (??) if we set $d=ap +bq +cr$ . So, after computing $d$ , we can proceed as in the sections above.

4. Finding New Coordinates

We get the new coordinates of $\boldsymbol{Z'}$ by projecting it onto the unit vectors $\boldsymbol{e_1}$ and $\boldsymbol{e_2}$ :

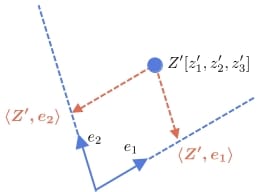
To do that, it’s sufficient to find the dot products $\langle Z', e_1 \rangle$ and $\langle Z', e_2 \rangle$ .

Now, let’s suppose that $e_1 = [e_{11}, e_{12}, e_{13}]$ and $e_2=[e_{21}, e_{22}, e_{23}]$ . If we treat all the vectors (including points) as column vectors, we can get the new coordinates of $Z'$ by matrix multiplication:

(4) $\begin{equation*} \begin{bmatrix} e_{11} & e_{12} & e_{13} \\ e_{21} & e_{22} & e_{23} \\ \end{bmatrix} \times \begin{bmatrix} z_1' \\ z_2' \\ z_3' \end{bmatrix} = \begin{bmatrix} e_{11} z_1' + e_{12} z_2' + e_{13} z_3' \\ e_{21} z_1' + e_{22} z_2' + e_{23} z_3' \\ \end{bmatrix} \end{equation*}$