Introduction to Spire

1. Overview

In this tutorial, we’ll explore Scala Spire. It’s a library focused on providing performant and generic numeric types.

First, we’ll have a tour of Spire basics, namely its number types and high-level type classes. Then, we’ll dive into the library’s low-level algebraic structures. Finally, we’ll learn about some useful macros.

2. Motivation

Spire is a numerical library that aims to solve four main issues in the Scala math ecosystem.

First, it addresses the lack of numeric abstractions. In fact, it’s hard to write an algorithm that works the same way for different numeric types – we’d either duplicate the implementation for each targeted type or write inefficient generic code.

Spire fixes those limitations by introducing new generic number types and algebraic structures:

def gcd[T](a: T, b: T)(implicit ev: Integral[T]) = ev.gcd(a, b)

Thanks to the Spire Integral type, we can calculate the greatest common divisor of three different number types using the same algorithm. The Integral type provides a set of algebraic operations for Int, BigInt, and Long number types. Spire already has all the required implicits within the spire.implicits package.

Second, the library addresses the performance of numeric algorithms. For most cases, Scala generics are slow. Using them for a large range of numbers can result in poorly optimized code. This benchmark from the Spire creators proves it:

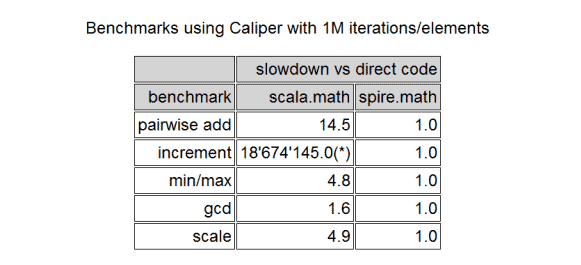
We observe that Spire is more performant than the standard Scala math library for most numeric operations. To increase performance, Spire uses rich language features such as macros and specialization.

Third, Spire promotes numerical precision. It’s important to use the right number type for the right operation. By introducing Rational, Spire makes sure that operations on rationals give the right output:

val r1 = Rational(1, 3)
val r2 = Rational(1, 2)
val result = r1 + r2

The result of this addition is 5/6. This is a precise addition under the rational type.

Finally, Spire adds convenient features that are missing in the language. For instance, we can’t easily perform floor, rounding, or logarithm on BigDecimal. Scala fixes that and many other issues by adding common math methods to its new number types.

Overall, Spire helps us write efficient, abstract, accurate, and performant numeric algorithms in Scala.

3. Setup

Let’s start by adding the Spire dependency:

libraryDependencies += "org.typelevel" %% "spire" % "0.18.0"

It’s important to note that before version 0.14.0, Spire used the org.spire-math group.

4. Number Types

Spire introduces a variety of number types. These types come in different flavors, from exact to approximate ones. Let’s have an overview of them.

4.1. Natural

First, the Natural type represents non-negative integers, including zero. It’s preferred to Int or Long for operations on maximum 128-bit values. Past that size, SafeLong or BigInt are faster. Natural also supports ordering:

val a: Natural = Natural(42)
val b: Natural = Natural(10)
val comparison: Int = a.compare(b)
val isALessThanB: Boolean = a.<=(b)
val isAGreaterThanB: Boolean = a.>=(b)

Here, the compare() method returns 1, which means Natural a is greater than b.

4.2. Rational

Second, the Rational type represents rational numbers as a ratio of two Longs. It’s closed under division. Consequently, Rational also provides exact results. We can further tune them to a desired scale to get decimal approximations:

val rational = Rational(1) / Rational(3)
val approximation = rational.toBigDecimal(5, RoundingMode.UP)

With a scale of 5, we get 0.33334 as an accurate approximation of the rational 1/3.

4.3. Real

Third, we have the Real type. It’s an approximation of real numbers. Particularly, Real will behave like Rational for rational reals. For irrational values, it gives an approximation with the desired precision. Consequently, irrational reals are expensive to compute. Besides, Real supports trigonometric operations:

val PI = Real(16) * atan(Real(Rational(1, 5))) - Real(4) * atan(Real(Rational(1, 239)))

This is a decent approximation of PI using a Machin-like formula. It gives us 3.1415926535897932384626433832795028841972.

4.4. Complex

Next, the Complex number type represents complex numbers. It’s optimized for Float and Double. Complex doesn’t support ordering. That’s in concordance with its algebraic properties:

def quadraticRoots(x: Complex[Double], y: Complex[Double], z: Complex[Double]): (Complex[Double], Complex[Double]) = {
  val discriminant = y * y - Complex(4.0) * (x).*(z)
  val sqrtDiscriminant = discriminant.sqrt
  val r1 = (-y + sqrtDiscriminant) / (Complex(2.0) * x)
  val r2 = (-y - sqrtDiscriminant) / (Complex(2.0) * x)
  (r1, r2)
}

This function calculates the roots of a quadratic equation that has three complex coefficients x, y, and z.

4.5. Interval

Finally, Interval[T] provides arithmetic on intervals for any ordered number type T. We can check if a particular number is in the interval or do arithmetic on two intervals:

val interval1 = Interval.closed(1, 4)
val interval2 = Interval.open(2, 7)
val union = interval1.union(interval2)
val intersection = interval1.intersect(interval2)
val contains3 = intersection.contains(4)
val contains7 = union.contains(7)
val isSubset = intersection.isSubsetOf(interval2)

It’s noticeable that interval bounds can each be open or closed. In our code above, the intersection (2, 4] is open on the lower bound and closed on the upper one. Consequently, it contains its upper bound and is a subset of inverval2.

Globally, Spire offers a wide range of number types. It’s worth noting that Polynomial is very useful for doing arithmetic on polynomials. Additionally, the Algebraic type is optimized for accurate number comparisons and n-root algorithms.

Besides, the Number type can be used for simple calculations. It’s always guaranteed to provide correctness for all the underlying types it wraps. In case we need more speed, we can directly tap into one of its sub-types.

5. Type Classes

Most Spire number types are built around algebraic structures. Those structures are represented as specialized type classes. The combination of specialization and implicits makes them fast for most use cases. Let’s review some of the Spire type classes.

5.1. Numeric, Fractional, and Integral

Spire has three high-level type classes: Numeric, Fractional, and Integral.

First, Integral defines arithmetical operations for all integers:

def factorial[@specialized(Int) T](n: T)(implicit integral: Integral[T]): T = {
  if (integral.lt(n, integral.one)) integral.one
  else integral.times(n, factorial(integral.minus(n, integral.one)))
}

Our factorial() function computes the factorial of any Int or BigInt. It’s specialized on Int for faster computation.

Second, Fractional operates on Decimal and Rational number types:

def avg[T](values: List[T])(implicit fractional: Fractional[T]): T = {
  val sum = values.foldLeft(fractional.zero)(fractional.plus)
  fractional.div(sum, fractional.fromInt(values.length))
}

This avg() function calculates the average of any list of Double, Rational, or BigDecimal. foldLeft() sums the value of the list starting with zero.

Finally, Numeric defines operations for every numeric type like Interval and Complex. It also has implicits that allow us to mix literal and generic values:

def sum[T](values: List[T])(implicit numeric: Numeric[T]): T = {
  values.foldLeft(numeric.zero)(numeric.plus)
}

We can apply our custom sum() function to any number type. It’s guaranteed to give the best result possible. Let’s keep in mind that we should use more precise type classes than Numeric if we need accurate results.

5.2. Groups

SemiGroup and Monoid are the most basic algebraic type classes in Spire.

First, a SemiGroup defines the law of associativity on any type T that uses a binary operator |+| . Concretely, Semigroup provides a combine() method to perform the |+| operation on two instances of a type T:

val a: Int = 5
val b: Int = 7
val result: Int = Semigroup[Int].combine(a, b)

We’ve performed an addition on two integers. The binary operator here is plus or +. Under the hood, Spire defines all the necessary implicits.

Next, a Monoid is a SemiGroup where the given type T has an identity element called empty:

combine(x, empty) == combine(empty, x) == x

Any combination of an instance of T with the empty element leaves it unchanged. A particular Monoid that focuses on the addition operation is the AdditiveMonoid:

def sum[T](values: List[T])(implicit ev: AdditiveMonoid[T]): T =
  values.foldLeft(ev.zero)(ev.plus)

The neutral element here is zero, and the operation is plus(). With this function, we’re able to sum any list of Int or BigDecimal.

Finally, the Group type class adds an inverse() operation to a Monoid . It guarantees that the combination of a number with its inverse results in the empty element. This allows operations like subtraction and division on Int, Natural, Rational, or Double. Let’s define a Transaction and TransactionGroup to manage the flow of money within a given bank account:

case class Transaction(amount: Int)

object TransactionGroup extends Group[Transaction] {
  def combine(x: Transaction, y: Transaction): Transaction = Transaction(x.amount + y.amount)
  def empty: Transaction = Transaction(0)
  def inverse(a: Transaction): Transaction = Transaction(-a.amount)
}

Our TransactionGroup binary operator is addition. The empty element is a transaction with an amount of zero. Now, let’s simulate deposits and withdrawals in our account:

class TransactionGroupUnitTest extends AnyWordSpec with Matchers {

  "TransactionGroup" should {
    val deposit = Transaction(1250)
    val withdrawal = Transaction(-450)
    val reversal = TransactionGroup.inverse(withdrawal)

    "calculate account balance" in {
      val balance = TransactionGroup.combine(deposit, withdrawal)
      assert(balance.amount == 800)
    }

As expected, the reversal and balance are correctly calculated.

5.3. Rings

First, the Ring type class adds addition and multiplication to a commutative Group. Let’s use a Ring to sum and square a list of integers:

implicit val IntRingInstance: Ring[Int] = new Ring[Int] {
  def zero: Int = 0
  def one: Int = 1
  def plus(x: Int, y: Int): Int = x + y
  def times(x: Int, y: Int): Int = x * y
  def negate(x: Int): Int = -x
}

def square(ints: Int*): Seq[Int] = {
   ints.map(i => Ring[Int].times(i, i))
}

def sum(ints: Int*): Int = {
  ints.foldLeft(Ring[Int].zero)(Ring[Int].plus)
}

The IntRingInstance provides operations used in our two functions. Particularly, times() refers to multiplication, and plus() to addition.

Next, Spire introduces the EuclideanRing. It’s a commutative Ring that supports GCD, LCD, quotient, and modulus operations. It’s important to note the difference between equot and equotmod  operations. The first returns the quotient resulting from an integer division. On the other hand, equotmod includes the remainder in the final result:

def equotient(dividend: Int, divisor: Int): Int = EuclideanRing[Int].equot(dividend, divisor)
def equotientmod(dividend: Int, divisor: Int): (Int, Int) = EuclideanRing[Int].equotmod(dividend, divisor)

For a dividend of 10 and a quotient of 3, quotient() returns 3 while equotientmod() returns (3,1).

Finally, a Field extends EuclideanRing by including division. But it doesn’t support n-root, trigonometric operations, and ordering.

Except for comparison operators, Ring, EuclideanRing, and Field are respectively similar to Numeric, Integral, and Fractional.

6. Macros

Spire has a handful of macros that ease the developer experience with the library. Let’s go through some of them.

6.1. Literal Number Syntax

Literal number syntax provides a short and convenient way to declare Spire number types. They’re evaluated at compile-time:

val poly1 = poly"3x^2 - 5x + 1"
val poly2 = poly"5/4x^6 - 7x - 2"
val poly3 = poly1.-(poly2)

We’ve declared two instances of the Polynomial type and computed their difference. The result is still a polynomial since literals are type-safe.

6.2. cfor() Macro

Spire introduces a convenient cfor() macro to loop through a range of numbers. It’s specifically designed to optimize loop performance by eliminating unnecessary object allocations and method calls:

cfor(9)(_>=0, _-1) { i =>
  println(i)
}

Here, we print all numbers from 9 to 0. The cfor() macro comes in handy when manipulating large numbers or performing critical computations.

7. Conclusion

In this article, we learned about the Scala Spire library. First, we looked at the many number types it introduces. Then we saw the type classes that power them. Finally, we explored the library’s macros.

Spire offers more features. These include sorting algorithms and pseudo-random number generators.

As always, the source code for the examples is available over on GitHub.