1. Introduction
In this tutorial, we’ll showcase the immutable BitSet and its usage in Scala.
BitSet is a data structure that enables us to perform bit operations on many bits quickly and efficiently. For example, we use BitSets for 2D collision detection in video games and instead of boolean arrays in bloom filter implementations. Although BitSets are not commonly used, they are often used in libraries to enable compactness and speed.
2. Under the Hood
Internally, a BitSet stores its bits in a Long Array. In this way, the first 64 bits are stored in the first Long of the Array; then the next 64 bits are stored in the second Long of the Array, etc.:
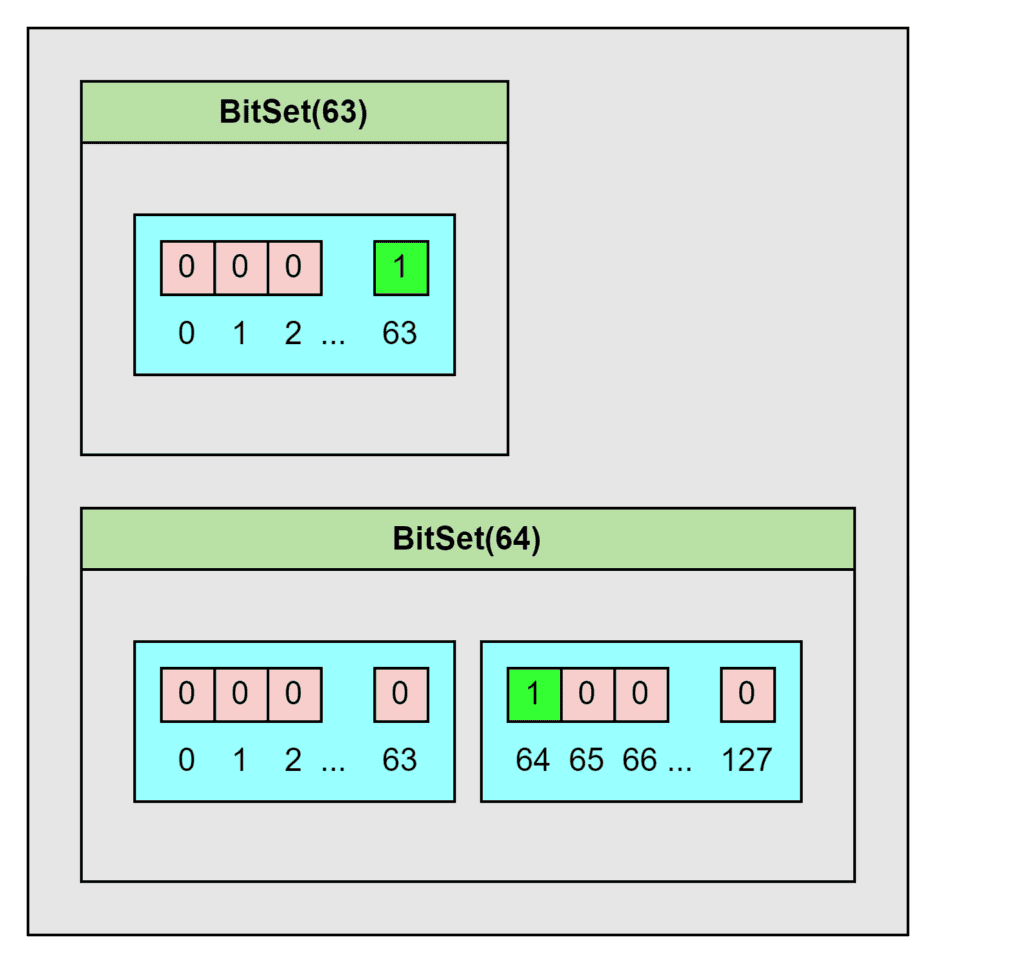
Internally, the Long Array is memory efficient as long as the numbers are relatively small. Indeed, using Long, a 64-bit data type, the internal Array size is as small as possible. In contrast, if the internal Array stored integers, the array size would be multiplied by two since Int is a 32-bit data type. This is illustrated by the diagram above, where the second element is added to the Array when the number 64 is added in the BitSet. We refer to the elements of this internal array as words.
Another integral part of a BitSet is its bit mask. A bit mask refers to the Long numbers that hold the internal representation of the bits representing the underlying set.
Not unexpectedly, bit masks containing the Long number representation are easier to read than the binary representation.
3. Common Operations With BitSet
Now that we better understand BitSet and how it works, it’s time to demonstrate their use.
3.1. Initialization
First of all, let’s create an empty BitSet instance:
"create an empty instance" in {
assert(BitSet() === BitSet.empty)
}Additionally, non-empty BitSets are initialized via the apply method, by using the SetOps trait operators, by using the incl function:
"create an non-empty instance when arguments are provided" in {
assert(BitSet(2) === BitSet() + 2)
assert(BitSet(2) === BitSet().incl(2))
}3.2. Contains
To verify if an element is present in a BitSet, we use the method contains:
"BitSet.contains" should {
"return true for existing elements" in {
assert(BitSet(3, 4).contains(3))
}
"return false for non-existing elements" in {
assert(!BitSet(3, 4).contains(12))
}
}To make our examples easier to understand, we first need to describe in simple terms what BitSet(3, 4) means. When we use the BitSet(x,y,z) or BitSet.apply(x,y,z), the bit at each specified index is set to 1 – so in our case of 3, 4, the 3rd and 4th bit are the only bits set to 1, and every other bit is set to 0.
As expected, the first assertion asserts that contains(3) returns true since 3 is included in the BitSet, while the second assertion asserts that contains(12) returns false because 12 is not in the set.
3.3. Include and Exclude
As the names imply, incl and excl functions include or exclude an element from the set.
Let’s write a test case to demonstrate incl and excl behavior:
"BitSet.excl" should {
"remove an element if present" in {
assert(BitSet(3, 4).excl(3) === BitSet(4))
assert(BitSet(4).excl(3) === BitSet(4))
}
}
"BitSet.incl" should {
"include an element if not present" in {
assert(BitSet(3).incl(4) === BitSet(3, 4))
assert(BitSet(3, 4).incl(3) === BitSet(3, 4))
}
}3.4. Difference, Concatenate, and Union
The diff function returns a new BitSet representing the difference between two BitSets. Having said that, for two given BitSets, b1 and b2, the call to diff will return only elements that are present in b1 and not in b2:
"BitSet.diff" should {
"return the difference of two BitSet instances" in {
assert(BitSet(3, 4).diff(BitSet(2, 3)) == BitSet(4))
}
"return an empty BitSet for equal sets" in {
assert(BitSet(3, 4).diff(BitSet(3, 4)) == BitSet.empty)
}
}On the other hand, the concat method returns a new BitSet, including every element from two BitSets:
"BitSet.concat" should {
"return a BitSet containing the elements of both sets" in {
assert(BitSet(3, 4).concat(BitSet(2, 3)) == BitSet(2, 3, 4))
}
}Like the concat function, the union function also returns a new BitSet containing every element of two BitSets:
"BitSet.union" should {
"return a BitSet containing the elements of both sets" in {
assert(BitSet(3, 4).union(BitSet(2, 3)) == BitSet(2, 3, 4))
assert(
BitSet(3, 4).union(BitSet(2, 3)) == BitSet(3, 4).concat(BitSet(2, 3))
)
}
}3.6. Intersect and Xor
In terms of set theory, the intersection of sets A and B is a set that contains elements that are present at A and B. As expected, the intersect function implements the functionality we just described:
"BitSet.intersect" should {
"return a BitSet containing only elements existing in both sets" in {
assert(BitSet(3, 4).intersect(BitSet(2, 3)) == BitSet(3))
}
}On the contrary, elements that aren’t present in both sets are obtainable via the xor function:
"BitSet.xor" should {
"return a BitSet containing only elements existing in either set1 or set2" in {
assert(BitSet(3, 4).xor(BitSet(2, 3)) == BitSet(2, 4))
}
}3.7. Bit Masks
As already described, a bit mask is a less verbose way to describe a BitSet. To obtain a bit mask, we use the toBitMask method:
"BitSet.toBitMask" should {
"return an array containing the words that are stored internally" in {
assert(BitSet(3, 4).toBitMask.sameElements(List(24)))
}
}Admittedly, the above snippet isn’t self-explanatory, so let’s elaborate. A BitSet(3, 4) translates to an underlying binary representation of three zeros and two ones followed by 59 zeros. Also, the binary representation we just described equals the decimal 24 (2^3 + 2^4); hence, the toBitMask function returns an array with the number 24.
Conversely, the fromBitMask method yields a BitSet with an internal array of words containing the given argument:
"BitSet.fromBitMask" should {
"return a BitSet containing internally as words the given arguments" in {
assert(BitSet.fromBitMaskNoCopy(Array(25L)) == BitSet(0, 3, 4))
}
}Again, the above test case succeeds since 2^0 + 2^3 + 2^4 equals 25.
4. Conclusion
In this article, we presented the BitSet data structure, its uses, and its applications. While most of the applications we develop won’t benefit from BitSets, it’s important to remember BitSets and how they work, especially when it comes to performing caching or other performance-critical operations.
As always, the code for this article is available over on GitHub.