1. Introduction
In this tutorial, we’ll learn how to implement Dijkstra’s algorithm in Kotlin. It stands out as a solution for uncovering the shortest path from a starting node to all other nodes within a graph. Unlike the Breadth-First Search (BFS), which is suitable for unweighted graphs, Dijkstra’s algorithm excels in environments with weighted edges, optimizing the path based on cumulative weight or distance. This article dives into implementing Dijkstra’s algorithm in Kotlin, showcasing the language’s succinct syntax and robust capabilities.
2. Understanding Dijkstra’s Algorithm
Dijkstra’s algorithm excels at finding the shortest path from a starting node to all other nodes in a graph with weighted edges. It initializes the start node distance to zero and others to infinity, iteratively updating distances and processing nodes in ascending order of their distance.
Dijkstra’s algorithm functions optimally with directed and undirected graphs containing positive weights. It doesn’t accommodate negative edge weights, as these can lead to inconsistencies in path length calculations, potentially causing infinite loops. Moreover, the algorithm may not perform as intended in graphs with loops or disconnected segments, necessitating additional checks or modifications to handle such complexities.
3. Implementing Dijkstra’s Algorithm in Kotlin
Dijkstra’s algorithm begins with setting the distance from the start node to zero and all other nodes to infinity. It iteratively selects the unvisited node with the smallest known distance from the start node, updates the distances to its adjacent nodes, and repeats this process until all nodes have been visited. This prioritization of the next closest node is a stark contrast to BFS’s level-by-level neighbor exploration, necessitating a priority queue to efficiently manage node processing.
3.1. Defining a Graph
To implement Dijkstra’s algorithm, we first need a graph with weighted edges. We represent this graph in Kotlin using an adjacency list, where each node is associated with a list of pairs. Each pair contains a connected node and the weight of the edge between them. Here’s a visual representation of such a graph:
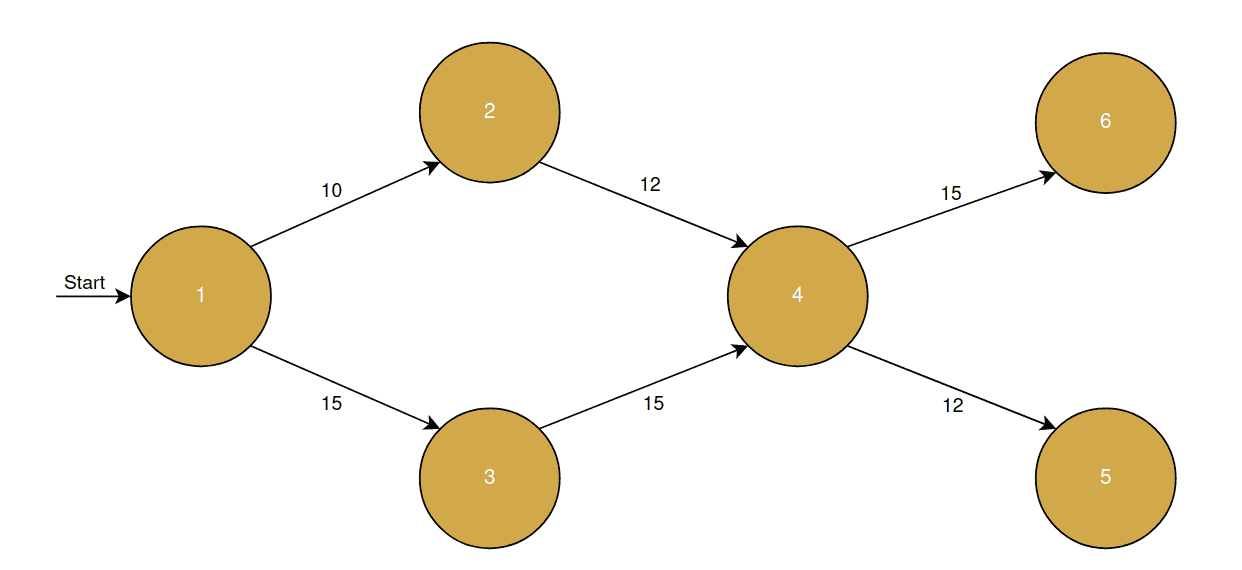
Based on this structure, we can define our graph in Kotlin as follows:
val graph = mapOf<Int, List<Pair<Int, Int>>>(
1 to listOf(Pair(2, 10), Pair(3, 15)),
2 to listOf(Pair(4, 12)),
3 to listOf(Pair(4, 15)),
4 to listOf(Pair(5, 12), Pair(6, 15)),
5 to emptyList(),
6 to emptyList()
)
This adjacency list allows us to efficiently store and access the graph’s connections and weights. It’s the foundation for our Dijkstra’s algorithm implementation.
3.2. The Algorithm
With our graph structure, we delve into the algorithm. A priority queue and a distance map are pivotal, storing the shortest discovered distances and controlling node processing order:
fun dijkstra(graph: Map<Int, List<Pair<Int, Int>>>, start: Int): Map<Int, Int> {
val distances = mutableMapOf<Int, Int>().withDefault { Int.MAX_VALUE }
val priorityQueue = PriorityQueue<Pair<Int, Int>>(compareBy { it.second }).apply { add(start to 0) }
distances[start] = 0
while (priorityQueue.isNotEmpty()) {
val (node, currentDist) = priorityQueue.poll()
graph[node]?.forEach { (adjacent, weight) ->
val totalDist = currentDist + weight
if (totalDist < distances.getValue(adjacent)) {
distances[adjacent] = totalDist
priorityQueue.add(adjacent to totalDist)
}
}
}
return distances
}
In this implementation, distances map stores the shortest path from the start node to every other node, initialized with a default value of Int.MAX_VALUE. A priority queue orders nodes by their distance, ensuring it processes the nearest nodes first. As the algorithm processes nodes, it updates the distance map for each node’s neighbors if it finds a shorter path, continuously refining the path until it establishes the shortest distances to all nodes.
3.3. Handling Loops
When implementing Dijkstra’s algorithm in Kotlin, we must give special consideration to handling graphs that contain loops. Loops in a graph can complicate the calculation of the shortest path because they allow revisiting a node with a potentially lower cumulative weight. It’s crucial to ensure that our implementation effectively manages these scenarios to maintain the algorithm’s accuracy and prevent infinite loops during execution. There are three main steps to follow when handling loops in Djikstra:
- Detecting Loops: During the execution of the algorithm, we should check if a node has already been visited and if visiting it again would offer a shorter path. If a node is revisited and no shorter path is found, it should not be added again to the priority queue.
- Updating Distances: If a loop is detected and revisiting the node results in a shorter path, the distance to this node should be updated, and the node should be re-enqueued with the new distance. This ensures that the algorithm always considers the shortest path to each node, even if that path involves traversing a loop.
- Preventing Infinite Loops: To prevent the algorithm from falling into an infinite loop, we can maintain a set that tracks each node and the distance at which it was added to the queue. Before adding a node back into the queue, check if it exists in the set with a higher distance. If not, it’s safe to re-enqueue the node; otherwise, skip adding it to prevent redundant operations.
Let’s adapt our algorithm and create dijkstraWithLoops():
fun dijkstraWithLoops(graph: Map<Int, List<Pair<Int, Int>>>, start: Int): Map<Int, Int> {
val distances = mutableMapOf<Int, Int>().withDefault { Int.MAX_VALUE }
val priorityQueue = PriorityQueue<Pair<Int, Int>>(compareBy { it.second })
val visited = mutableSetOf<Pair<Int, Int>>()
priorityQueue.add(start to 0)
distances[start] = 0
while (priorityQueue.isNotEmpty()) {
val (node, currentDist) = priorityQueue.poll()
if (visited.add(node to currentDist)) {
graph[node]?.forEach { (adjacent, weight) ->
val totalDist = currentDist + weight
if (totalDist < distances.getValue(adjacent)) {
distances[adjacent] = totalDist
priorityQueue.add(adjacent to totalDist)
}
}
}
}
return distances
}
4. Testing
To validate our Dijkstra’s algorithm implementation, we create a test scenario reflecting our graph structure:
@Test
fun `Should calculate shortest path when using Dijkstra algorithm`() {
val graph = mapOf(
1 to listOf(Pair(2, 10), Pair(3, 15)),
2 to listOf(Pair(4, 12)),
3 to listOf(Pair(4, 15)),
4 to listOf(Pair(5, 12), Pair(6, 15)),
5 to emptyList(),
6 to emptyList()
)
val shortestPaths = dijkstra(graph, 1)
assertEquals(37, shortestPaths.getValue(6))
}
In this test, we assert that the shortest path from node 1 to node 6 is 37, demonstrating the algorithm’s capability to calculate minimum distances. Through unit testing, we ensure the reliability and efficiency of Dijkstra’s algorithm implementation in Kotlin.
6. Conclusion
Dijkstra’s algorithm in Kotlin provides a robust and efficient method for finding the shortest path in weighted graphs. By leveraging Kotlin’s features, we can implement this classic algorithm with clarity and precision, enabling the development of sophisticated applications. As always, the code used in this article is available over on GitHub.
