Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 19, 2024
In this tutorial, we’ll implement the basic operations for a binary tree using the Kotlin programming language.
Feel free to check our Java version of this same tutorial.
In programming, a binary tree is a tree where every node has no more than two child nodes. Every node contains some data that we call a key.
Without loss of generality, let’s limit our consideration to the case when the keys are just integer numbers.
So, we may define a recursive data type:
class Node(
var key: Int,
var left: Node? = null,
var right: Node? = null)That contains a value (the integer-valued field key) and optional references to a left and a right child that are of the same type as their parent.
We see that due to the linked nature, the whole binary tree can be described by just one node that we will call a root node.
Things become more interesting if we apply some restrictions on the tree structure. In this tutorial, we suppose that the tree is an ordered binary tree (also known as a binary search tree). This means the nodes are arranged in some order.
We suppose that all of the following conditions are part of our tree’s invariant:
Some of the most common operations include:
When the tree is ordered, the lookup process becomes very efficient: if the value to search is equal to the current node’s one, then the lookup is over; if the value to search is bigger than the current node’s one, then we may discard the left subtree and consider only the right one:
fun find(value: Int): Node? = when {
this.value > value -> left?.findByValue(value)
this.value < value -> right?.findByValue(value)
else -> this
}Note that the value might not be present among the tree’s keys and hence the result of the lookup might return a null value.
Note, how we have used the Kotlin keyword when which is a Java analog of the switch-case statement but much more powerful and flexible.
Since the tree does not allow any duplicate keys, it is quite easy to insert a new value:
So, we may recursively parse the tree in search of a subtree that should accommodate the value. When the value is less than the key of the current node, pick its left subtree if it is present. If it is not present, it means the location to insert the value is found: this is the left child of the current node.
Similarly, in the case when the value is greater than the key of the current node. The only remaining possibility is when the value is equal to the current node key: it means that the value is already present in the tree and we do nothing:
fun insert(value: Int) {
if (value > this.key) {
if (this.right == null) {
this.right = Node(value)
} else {
this.right.insert(value)
}
} else if (value < this.key) {
if (this.left == null) {
this.left = Node(value)
} else {
this.left.insert(value)
}
}First, we should identify the node that contains the given value. Similar to the lookup process, we scan the tree in search of the node and maintain the reference to the parent of the sought node:
fun delete(value: Int) {
when {
value > key -> scan(value, this.right, this)
value < key -> scan(value, this.left, this)
else -> removeNode(this, null)
}
}There are three distinct cases that we may face when removing a node from a binary tree. We classify them based on the number of non-null child nodes.
Both child nodes are null
This case is quite simple to handle and it is the only one in which we may fail to eliminate the node: if the node is a root one, we can not eliminate it. Otherwise, it is enough to set to null the parent’s corresponding child.
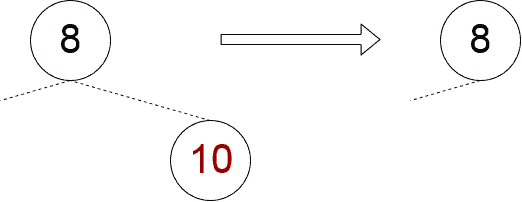
Implementation of this approach might look like this:
private fun removeNoChildNode(node: Node, parent: Node?) {
if (parent == null) {
throw IllegalStateException("Can not remove the root node without child nodes")
}
if (node == parent.left) {
parent.left = null
} else if (node == parent.right) {
parent.right = null
}
}One child is null, the other is not null
In this case, we should always succeed as it is enough to “shift” the only child node into the node that we are removing:
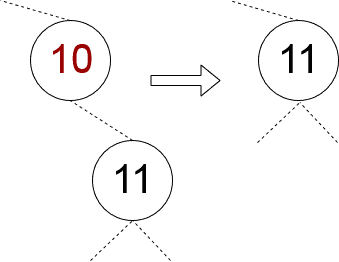
We may implement this case straightforwardly:
private fun removeSingleChildNode(parent: Node, child: Node) {
parent.key = child.key
parent.left = child.left
parent.right = child.right
}Both child nodes are not null
This case is more intricate as we should find a node that is to replace the node we want to remove. One way to find this “replacement” node is to pick a node in the left subtree with the biggest key (it for sure exists). Another way is a symmetric one: we should pick a node in the right subtree with the smallest key (it exists as well). Here, we choose the first one:
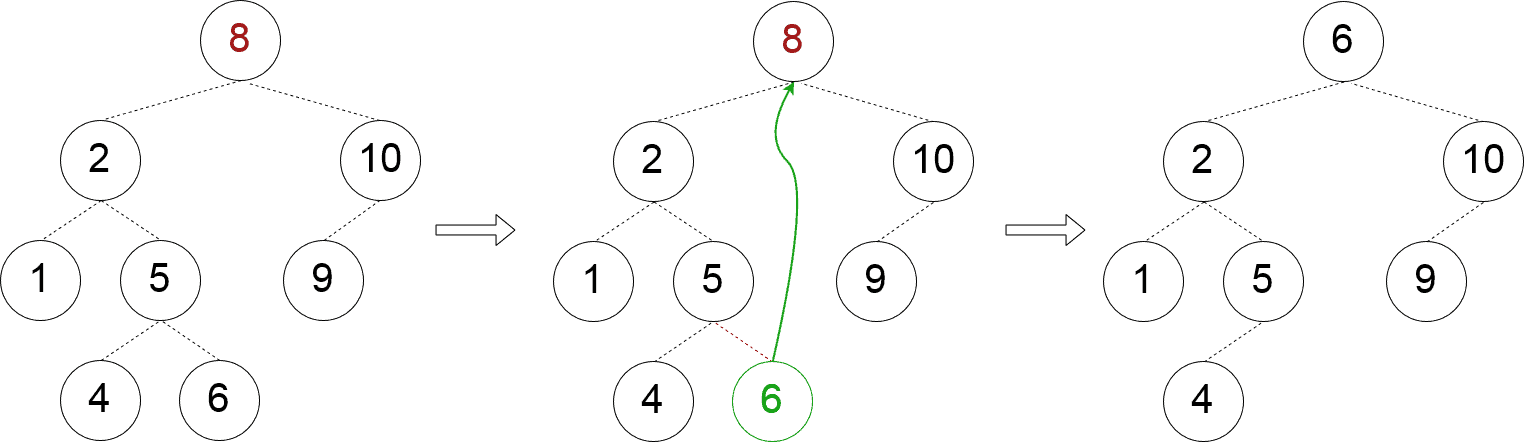
Once the replacement node is found, we should “reset” the reference to it from its parent. It means that when searching for the replacement node, we should return its parent as well:
private fun removeTwoChildNode(node: Node) {
val leftChild = node.left!!
leftChild.right?.let {
val maxParent = findParentOfMaxChild(leftChild)
maxParent.right?.let {
node.key = it.key
maxParent.right = null
} ?: throw IllegalStateException("Node with max child must have the right child!")
} ?: run {
node.key = leftChild.key
node.left = leftChild.left
}
}There are various ways of how the nodes may be visited. Most common are depth-first, breadth-first, and level-first search. Here, we consider only depth-first search which can be of one of these kinds:
In Kotlin, all these kinds of traversal can be done in quite a simple way. For example, for the pre-order traversal, we have:
fun visit(): Array<Int> {
val a = left?.visit() ?: emptyArray()
val b = right?.visit() ?: emptyArray()
return a + arrayOf(key) + b
}Note, how Kotlin allows us to concatenate arrays by using “+” operator. This implementation is far from being an efficient one: it is not a tail-recursive and for a deeper tree we may run into the stack overflow exception.
In this tutorial, we considered how to construct and implement basic operations for a binary search tree using Kotlin language. We demonstrated some Kotlin constructs that are not present in Java and that we might find useful.