1. Introduction
In this tutorial, we’ll cover recursive and iterative algorithms for enumerating all k-combinations of a set.
2. Combinations
A combination is a subset of a set. So, in this problem, we have a set with
elements and want to list all its subsets with exactly
items.
Unlike permutations, the order in which we choose the individual elements doesn’t matter. Instead, we’re interested in whether a particular element is in a combination.
For example, we don’t care about the order in which we selected five cards out of 52; we only care about which cards are in hand.
3. Recursive Algorithm 1: Partitioning by Elements in the Original Set
Recursive algorithms partition the problem into smaller sub-problems of the same type and combine their solutions to get the solution to the original problem. We differentiate between recursive algorithms based on their partitioning schemes.
We’ll discuss two approaches. The first partitions the problem by the elements in the original set , whereas the other partitions by the selected elements.
3.1. Idea
We can partition the task by inspecting the set’s elements individually. For each item in the set, we can either include it in the selection or not.
So, we traverse the set in a predetermined order. If we include the first item (), we need to choose
elements from the remaining
items. On the other hand, if we discard
, we need to select
elements out of the remaining
items.
To solve the smaller problems (the selection of and
elements out of
), we apply the same partitioning scheme:
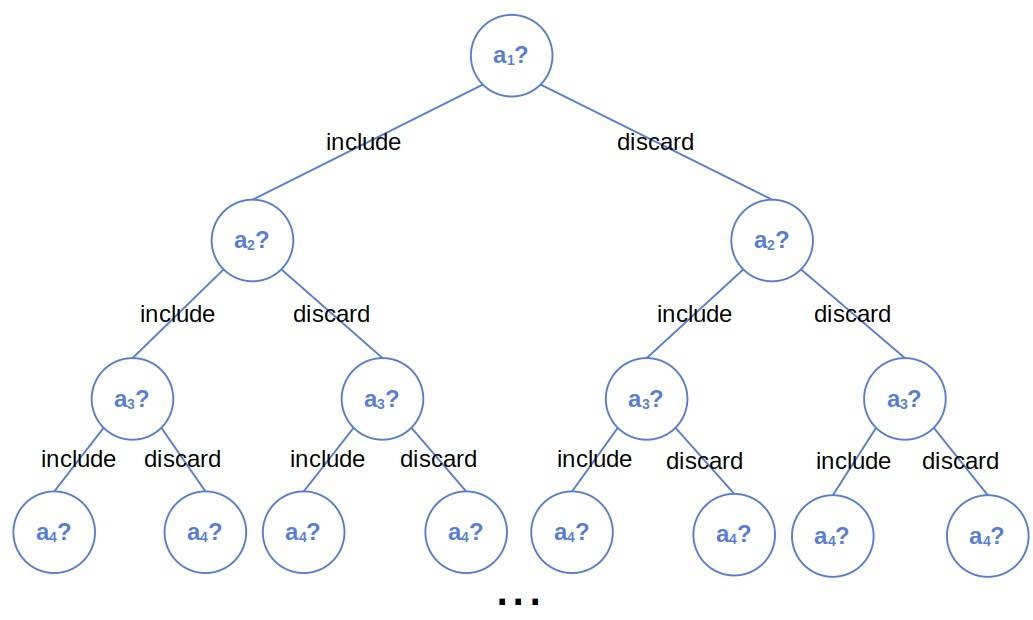
We can enumerate all -combinations by traversing the tree and collecting its leaves. At each step, we keep track of the elements in the currently active combination (which corresponds to the path from the root to the current node). Going down an edge, we remember the decision about including the node’s element; going up, we reverse the decision associated with the edge.
3.2. Pseudocode
Here’s the pseudocode:
means appending
to
.
The chosen order of elements determines the order of combinations at the output. Usually, we specify as an iterable data structure and call the order lexicographic. We denote it with the “less than” symbol:
.
3.3. Complexity and Issues
The time complexity of this approach is . This is so because there are
nested decisions about
elements, and each decision can have two outcomes. Therefore, this approach is inefficient if the input set is large.
Furthermore, it takes stack space. So, we may get a stack overflow if
is too big.
4. Recursive Algorithm 2: Partitioning by Elements in the Combination
Instead of tracking the elements in the input set, we can partition the problem by tracking the items in the selection.
4.1. Idea
Let’s assume we want to output ordered combinations. So, a -combination
should satisfy
, where
is the
th element of
.
To do so, the first item in a -combination must come from
. Otherwise, we can’t make an ordered combination.
If we choose as the first element, we can get an ordered combination only if we select the remaining
items from those to the right of
. In doing so, the first element in the
-combination must be from those to the left of
(or constructing a combination won’t be feasible). So, we iterate over the window
and repeat the process.
4.2. Pseudocode
Here’s the pseudocode:
In the above pseudocode, the for loop chooses the next item. Then, it calls the algorithm recursively for each position in the active window. We stop when the required number of items have been selected, output a combination, and go up the recursion tree to find other combinations.
If the right end of the current window goes beyond the array, we need to cap it. That’s why we have the step .
4.3. Complexity and Issues
The number of iterations corresponds to the sum of window sizes. Therefore, this number also equals the total number of times a window covered an element of .
We iterate over the element in a window of size
(
) if
items from
have already been selected. There are
ways of doing it, so the number of times
gets looped over is:
The ensures we count valid windows. For example, there’s no way to select two elements before
, and this condition is there to disregard such windows.
So, the total complexity is:
Although this algorithm is also exponential, its recursion tree is shallower than the first. It has levels, so the stack size complexity is
.
Therefore, this approach can work for large sets if the number of elements to be selected is less than the maximum call stack depth.
However, if is large, this method won’t work.
5. Iterative Algorithm
In the iterative approach, we start with the first lexicographic combination: . Then, we keep generating the next combination from the current one until we have generated all combinations.
5.1. Generating the Next Combination
To get the next combination from the current , we find the rightmost element of
that we can replace with a lexicographically larger element. The last element
is replaceable if it’s lexicographically smaller than
. Similarly, the second-to-last element
is replaceable if it’s lexicographically smaller than
.
So, the general rule is that is replaceable if it’s lower than
. The equivalent formulation is that
is replaceable if
.
Let’s say that the rightmost replaceable element of is at the
th position and equal to
. We replace the right sub-array
with
successors of
:
. This way, we get the next combination.
5.2. Pseudocode
We start with the first lexicographic -combination
:
The process stops when we get to the last lexicographic combination since it has no replaceable element.
5.2. Complexity
If is the rightmost replaceable element in
, generating the next combination takes
steps. So, the overall time complexity is:
where is the number of combinations in which the rightmost replaceable element is at the
th position.
Let’s find . If the rightmost replaceable is
, then
. So,
elements are fixed, and the left part contains
elements we can select from
. Therefore:
From there, we get the time complexity:
This reduces to:
Taking to be constant with respect to
, we get
. So, this algorithm has the same polynomial complexity as
, the number of
-combinations.
6. Conclusion
In this article, we explained three algorithms for generating combinations: two recursive and one iterative.
The recursive approaches might be easier to understand and code, but the iterative solution is the most efficient.