Tries (Prefix Trees)

1. Overview

In this tutorial, we’ll discuss the trie data structure, also called a prefix tree. We’ll briefly go through the basics and then see how to implement the most important features: insert, lookup, and prefix search.

2. What Is a Trie?

A trie or a prefix tree is a particular kind of search tree, where nodes are usually keyed by strings.

Tries can be used to implement data structures like sets and associative arrays, but they really shine when we need to perform an ordered traversal or to efficiently search for keys starting with a specific prefix.

For this reason, they are very often used when implementing features like autocompletion.

3. Trie Structure

In the basic implementation of a trie, each node contains a single character and a list of pointers to its children nodes. The key for the node is not explicitly stored: instead, we can derive it by computing the path from the root to the node.

Here’s what a trie looks like:

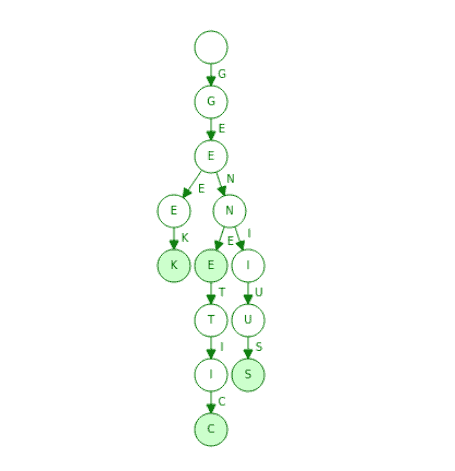
To distinguish which nodes in the tree represent valid keys, a boolean flag is used. Additionally, nodes can contain a pointer to arbitrary data, if we’re using the trie to implement an associative array data structure.

The figure shows a trie storing the keys “geek”, “genius”, “gene” and “genetic”, where highlighted nodes represent valid keys. By construction, all leaf nodes are valid keys, but for those who are not leaf nodes, we’ll need to set the boolean flag to true.

4. Insert an Element in a Trie

To insert an element into a trie, we need to start from the root node and traverse the tree down, only creating nodes when they’re missing. When we’ve created all necessary nodes, we’ll set the boolean flag to true on the last one.

For example, if the word “gene” is already contained in the tree, and we’re now inserting the word “genetic”, we’ll:

1. follow the “gene” path
2. create the additional nodes as needed for “t”, “i”, and “c”
3. mark the last “c” node as a valid key

Conversely, if the word “genetic” is already in the tree, and we’re now inserting the word “gene”, we won’t need to add any new node to the tree.

The only action to perform will be to mark the end node as a valid key:

algorithm insert(trie, key, value):
    // INPUT
    //    trie = the prefix tree
    //    key = the key to insert
    //    value = the value associated with the key
    // OUTPUT
    //    Inserts a node with the given key and value into the prefix tree.

    node <- trie.root
    
    for i <- 0 to key.length:
        char <- key[i]
        if not node.hasChild(char):
            node.addChild(char)
        node <- node.getChild(char)
    
    node.setValue(value)
    node.setKey(true)

5. Lookup

Lookup is used to see if a specific key is contained in the tree, and, if we’re implementing an associative array, to return the data associated with the key.

Let’s see the lookup algorithm:

algorithm lookup(trie, key):
    // INPUT
    //    trie = the prefix tree
    //    key = the key to lookup
    // OUTPUT
    //    Returns the node whose key matches the input, or null if not found.

    node <- trie.root
    
    for i <- 0 to key.length:
        char <- key[i]
        if not node.hasChild(char):
            return null
        node <- node.getChild(char)
    
    if node.isKey():
        return node
    else:
        return null

It’s very similar to the insert algorithm, but this time, when we find a missing node we’ll know that the value we’re looking for is not present. If the iteration has completed, it means we’ve found a matching path from the root to a node, and we just need to check if it’s a valid key.

Note that in both the insert and lookup algorithms, we never had to traverse the tree itself, using, for example, depth-first or breadth-first search. A traversal has never been needed because the path that we have to follow is provided in the input itself.

6. Prefix Search

We’ve seen the fundamental operations on a prefix tree. And, it’s now time to see where they excel, that is, retrieving all words with a given prefix from a vocabulary.

To do this, we’ll:

1. find the path of the prefix “P” in the tree, starting from the root
2. from the last node in the path “L”, compute all descendants of “L” which are valid keys
3. return the found nodes

Here’s how this looks in practice:

algorithm prefixSearch(trie, prefix):
    // INPUT
    //    trie = the prefix tree
    //    prefix = the prefix to search for
    // OUTPUT
    //    Returns a set of nodes whose keys start with the given prefix.
    
    if prefix.length = 0:
        return {}
    
    results <- {}
    
    node <- trie.root
    
    for i <- 0 to prefix.length:
        char <- prefix[i]
        if not node.hasChild(char):
            return {}
        node <- node.getChild(char)
    
    foreach d in node.getDescendants():
        if d.isKey():
            results.add(d)
    
    return results

7. Conclusions

In this article, we’ve seen how to implement a prefix tree data structure. Specifically, we learned how to implement basic insert and lookup operations as well as a prefix search functionality.