Sum of Digits in Factorial

1. Overview

In this tutorial, we’ll discuss an efficient approach to find the sum of digits in the factorial of a number. We’ll also present an algorithm and discuss the steps in detail.

2. Problem Statement

Given a number , we need to find the factorial of the number and then add the digits in the factorial.

Let’s take an example to understand the problem and the expected output. We’re taking a random number . So here . The first step is to calculate the factorial of .

The general formula for calculating the factorial of a number is . Now here :

The final step is to add the digits in the factorial.  For this example, the final result would be:

3. Our Approach

Given a number , we’ll calculate factorial using the previous formula. Next, we’ll take the factorial and find the last digit of the factorial. As soon as we find the last digit of the factorial, we’ll store it in a temporary variable (e.g., ) and remove the last digit from the factorial. We’ll repeat this process and continue adding the digits:

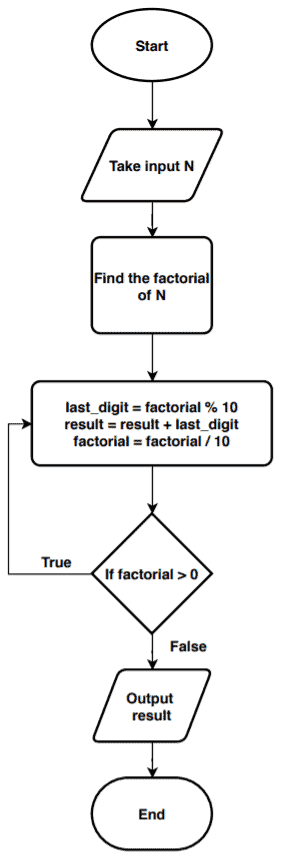
4. Pseudocode

Now let’s see the pseudocode:

algorithm SumFactorial(N):
    // INPUT
    //   N = a positive integer number
    // OUTPUT
    //   Sum of digits in the factorial of N

    factorial <- 1
    result <- 0

    for k <- 1 to N:
        factorial <- factorial * k

    while factorial != 0:
        last_digit <- factorial mod 10
        result <- result + last_digit
        factorial <- factorial / 10

    return result

Here we’re taking an integer number as an input. We use a variable to store the factorial of the input . The variable stores the last digits of the factorial. Finally, we’re adding the digits in the factorial of in the variable .

Now to remove the last digit from the at every iteration, we divide it with and reassign the quotient in .

5. Conclusion

In this tutorial, we showed how to find the sum of digits of a factorial. We discussed our approach and presented an algorithm to achieve the solution to the given problem.