Finding the Number of Distinct Subsequences of a String

1. Overview

In this tutorial, we’ll talk about the problem of finding the number of distinct subsequences of a string.

First, we’ll define the problem and provide an example to explain it. Then, we’ll present two different approaches to solving this problem and work through their implementations and space and time complexity.

2. Defining the Problem

Suppose we have a string $S$ , and we were asked to count the number of distinct subsequences in it.

Recall that a subsequence of a string is a sequence that can be derived from the given string by deleting zero or more elements without changing the order of the remaining elements.

Let’s take a look at the following example:

Given a string $S = "ABA"$ , let’s get all the distinct subsequences of that string (red squares represent the selected characters):

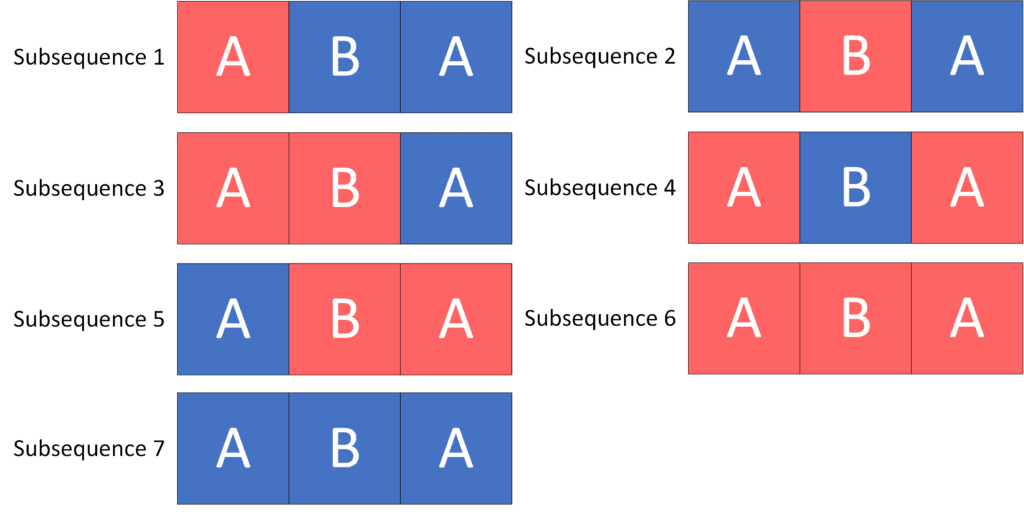
As we can see, there are $7$ different subsequences of the given string $S$ .

3. Naive Approach

3.1. Main Idea

The main idea in this approach is to generate all possible subsequences of the given string. Then, we put them into a set to get rid of the duplicates. In the end, the size of that set will be equal to the number of distinct subsequences we have.

Initially, we’ll have a backtracking method that will generate all the possible subsequences of the given string $S$ . Next, for each character in the given string, we’ll try to either pick it in the current subsequence or leave it. Then, when we reach the end of the string, we’ll have one potential subsequence. Thus, we append it to the set that will store the different subsequences.

Finally, the number of distinct subsequences of the given string $S$ will be equal to the size of the set.

3.2. Algorithm

Let’s take a look at the implementation of the algorithm:

Initially, we declare the $backtrack$ function to generate all possible subsequences of the given string $S$ . The function will have four parameters. $S$ is the string itself, and $index$ represents the current position in the given string $S$ . $cur\_ subsequence$ represents the current subsequence that we have until now, and $subsequences\_ set$ represents all possible distinct subsequences that we could generate from the given string $S$ .

First, the base case of the backtrack function is when we reach the end of the string $S$ , then we append the current $subsequence$ we have to $subsequences\_ set$ . Second, for each character, we have two choices:

Pick: We append the current character to the $subsequnce$ and move to the next one. When we’re back from that recursive call, we’ll backtrack on appending the character and pop the last character of the $cur\_ subsequence$ .
Leave: We just ignore the current character and move to the next one.

Finally, the size of the $subsequnces\_ set$ will be equal to the number of distinct subsequences of the given string $S$ .

3.3. Complexity

The time complexity of this algorithm is $\boldsymbol{O(2^N)}$ , where $N$ is the length of the given string $S$ . The reason is that for each character of the string, we have two options: to pick or leave it.

On the other hand, the space complexity of this algorithm is $\boldsymbol{O(M)}$ , where $M$ is the sum of the length of all possible subsequences of the given string $S$ . The reason behind this complexity is that for each possible subsequence, we’ll store it in the $subsequnces\_ set$ .

4. Dynamic Programming Approach

4.1. Main Idea

The main idea in this approach is to think about a formula to count the number of distinct subsequences of a string without generating those subsequences.

Initially, let’s say that $Count(N)$ represents the count of distinct subsequences that could be generated from the first $N$ characters of the given string. To compute $Count(N)$ , we’ll multiply $Count(N - 1)$ by $2$ since we have two options for each character of the given string: to pick or leave it. Then, we’ll subtract the number of duplicate subsequences that could be generated when adding the current character. Therefore, we can represent the previous idea in the following formula:

$\boldsymbol{Count(N) = 2 \times Count(N - 1) - Duplicates}$

The problem now is finding the number of duplicates. When we append the current character to the subsequence, we have two duplication cases:

If this is the first time that this character appears in the given string, then there are no subsequences that end with this character before. Thus, the number of duplicates is zero.
If this character appears before, then the number of duplicates equals the number of all subsequences that end at the last occurrence of this character. Formally, if $last[S_i]$ is the index of the last appearance to $S_i$ before $i$ , then the number of duplicates from adding the $i^{th}$ character is $Count[last[S_i]]$ .

Since this problem has overlapping states, we’ll use dynamic programming to solve it.

Finally, the $Count( Length(S) )$ will represent the number of distinct subsequences of the given string $S$ .

4.2. Algorithm

Let’s take a look at the implementation of the algorithm:

Initially, we have the $CountSubsequences$ function that will return the number of distinct subsequences of a string. It has one parameter $S$ , which represents the given string.

First, we declare the $DP$ array, which will store the number of distinct string subsequences up to a specific position. Also, we declare $last$ array which stores the position of the last time a specific character appears. Initially, all of its values equal $-1$ .

Second, we set the value of $DP[0]$ to $1$ , which represents the empty subsequence. Next, for each character, we have two options; either to pick or leave it. Therefore, we multiply the answer of the previous position by $2$ . Then, we check if the current character occurred before. If so, we subtract the answer of that position from the current answer. After that, we update the value of $last[S_i]$ to equal the current position.

Finally, the $DP[length(S)]$ will have the number of distinct subsequences of the given string $S$ .

4.3. Complexity

The time complexity of this algorithm is $\boldsymbol{O(N)}$ , where $N$ is the length of the given string $S$ . The reason behind this complexity is that we iterate over each character only once.

The space complexity of this algorithm is $\boldsymbol{O(N + A)}$ , where $N$ is the length of the given string $S$ and $A$ is the size of the alphabet. The reason is that for each position of the given string, we store the answer, and for each possible character, we store the index of the last time it appears.

5. Conclusion

In this article, we discussed the problem of finding the number of distinct subsequences in a given string. First, we provided an example to explain the problem. Then, we explored two different approaches to solve it, where the second one had a better time and space complexity.

Finally, we walked through their implementations and explained the idea behind each of them.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex